23. Частное натуральных чисел: определение и единственность. Свойства частного натуральных чисел

Опр.: Частным чисел и называется такое число , что . Обозначим .

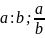Разное и частное не являются бинарными алгебраическими операциями.

Определение: Число кратно числу , если такое 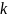, что .

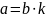Теорема: Если частное и 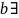, то оно единственное.

Доказательство:

.

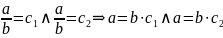
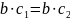
Свойство: .

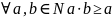Доказательство: .

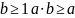Теорема: 1) 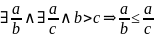; 2) .

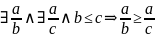Доказательство: 1)

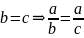
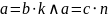
- пусть 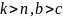- дано

- противоречие;

- пусть - дано

- противоречие;

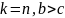- пусть - дано

.

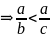24. Свойства сложения и вычитания для натуральных чисел: (а+в)-с=а+(в-с)

Теорема (свойство сложения и вычитания): Если соответствующая разность чисел 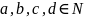, то выполняются следующие равенства:

1. ;

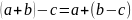Доказательство:

1)обозначим .

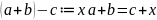Проверяем, подойдёт ли в качестве правая часть равенства

.

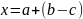
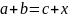
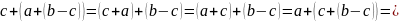
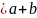25. Свойства сложения и вычитания для натуральных чисел: (а-с)-(в-с)=а-в

Теорема (свойство сложения и вычитания): Если соответствующая разность чисел , то выполняются следующие равенства:

1. ;

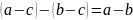Доказательство:

1)

.

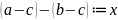
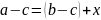
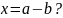
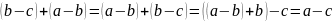26. Свойства сложения и вычитания для натуральных чисел: .

Теорема (свойство сложения и вычитания): Если соответствующая разность чисел , то выполняются следующие равенства:

1. .

Доказательство:

1)

.

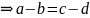
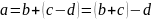
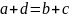
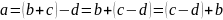
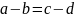27. Суммы и произведения нескольких натуральных чисел. Обобщенный закон дистрибутивности. Степень натурального числа с натуральным показателем и ее свойства

Определение. Пусть nN, тогда сумма n натуральных чисел а₁, а₂, … , а_n обозначается 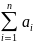и определяется индуктивно следующим образом:

1. 

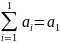
2. Если сумма определена для к натуральных чисел (k<n) то

Замечание. Если все слагаемые в определении равно а, то получим определение n-кратного числу а

na=

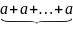
n раз

Определение. Пусть nN, тогда произведение n натуральных чисел а₁, а₂, … , а_n обозначается 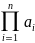и определяется индуктивно следующим образом:

1. 

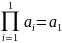
2. Если произведение определено для к натуральных чисел (k<n) то

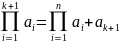
Замечание. Сумма и произведение нескольких натуральных чисел не зависит от того, как поставить скобки, а также от того, в каком порядке записать слагаемые (сомножители). Следует из свойств коммутативности, ассоциативности.

;

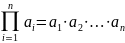
Теорема 1.

1.(

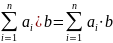
2.(

Доказательство:

1. ММИ(n)

n=2 (a₁+a₂)b=a₁b+a₂b

n=k (

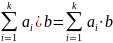
n=k+1 ( +

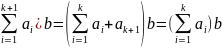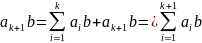
2. ММИ (m)

m=1

m=k

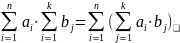
m=k+1

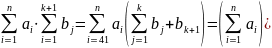
Свойство. a, u N na=na

Доказательство:

ММИ(n)

n=1 1a=a 1a=a1=a

n=k ka=ka

n=k+1 (k+1)a= =ka+a=ka+a=(k+1)a

k раз

Следcтвие. a, b, m, n N

1)(m+n)a=ma+na 2)(mn)a=m(na) 3)manb=(mn)(ab) 4)(m-n)a=ma-na 5)m(a+b)=ma+mb 6)m(a-b)=ma-mb

Доказательство:

1)ma+na=ma+na=(m+n) a=(m+n)a 2-6 самостоятельно.

Свойство. a, b, m, n N

1)a^m+n=a^maⁿ 2)a^mn=(a^m)ⁿ 3)a^m-n=a^maⁿ, если m>n 4)(ab)^m=a^mb^m 5)(ab)^m=a^mb^m , если частное существует.

Доказательство:

1. a^maⁿ=  = =

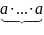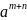
m раз n раз m+n раз