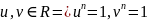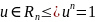- •1.Множество натуральных чисел n. Аксиомы Пеано
- •2.Независимость аксиом Пеано
- •3. Принцип полной математической индукции. Обобщенный принцип полной математической индукции. Примеры доказательства методом математической индукции
- •4. Сложение натуральных чисел как бинарная алгебраическая операция и как функция. Примеры. Свойство сокращения
- •5. Теорема о сложении натуральных чисел: единственность
- •6. Теорема о сложении натуральных чисел: существование
- •7.Ассоциативность сложения натуральных чисел
- •8. Коммутативность сложения натуральных чисел
- •Существование:
- •23. Частное натуральных чисел: определение и единственность. Свойства частного натуральных чисел
- •26. Свойства сложения и вычитания для натуральных чисел: .
- •27. Суммы и произведения нескольких натуральных чисел. Обобщенный закон дистрибутивности. Степень натурального числа с натуральным показателем и ее свойства
- •28. Равномощные множества. Отношение эквивалентности «быть равномощным». Отрезок натурального ряда. Конечные и бесконечные множества
- •29. Теорема о равномощности конечного множества только одному отрезку натурального ряда
- •30. Лемма о наибольшем и наименьшем элементе в конечном множестве. Бесконечность множества натуральных чисел
- •31. Счетность множеств целых и рациональных чисел. Несчетность множества действительных чисел
- •32. Отношение эквивалентности на множестве n2. Определение целого числа как класса эквивалентности на n2. Примеры
- •33. Определение суммы целых чисел и его корректность
- •34. Свойство сложения целых чисел
- •35. Определение произведения целых чисел и его корректность. Кольцо целых чисел и его свойства
- •38. Вложение множества натуральных чисел в кольцо целых чисел. Множество положительных целых чисел: определение, корректность определения, описание
- •40. Целое число как разность двух натуральных чисел. Отрицательные и положительные числа. Архимедовость и дискретность кольца целых чисел
- •41. Определение рациональных чисел как классов эквивалентности
- •42. Определение суммы рациональных чисел и его корректность. Аддитивная абелева группа рациональных чисел
- •43. Определение произведения рациональных чисел и его корректность. Поле рациональных чисел.
- •46. Вложение кольца целых чисел в поле рациональных чисел. Изоморфизм колец
- •47. Рациональное число как частное двух целых чисел. Поле рациональных как наименьшее поле, которое содержит кольцо целых чисел
- •49. Представление бесконечных периодических десятичных дробей обыкновенными дробями: правило, примеры
- •50. Определение действительных чисел как бесконечных десятичных дробей. Множество конечных десятичных дробей. Подходящие дроби
- •51. Определение и свойства отношения порядка на множестве действительных чисел
- •52. Плотность множества д в множестве действительных чисел
- •53. Определение и свойство суммы и произведения действительных чисел. Поле действительных чисел и его свойства
- •54. Определение, свойства и алгебраические операции с комплексными числами
- •55. Определение кватернионов. Алгебраические операции над кватернионами. Тело кватернионов
- •56. Вложение поля комплексных чиселв тело кватернионов. Теорема Фробениуса
54. Определение, свойства и алгебраические операции с комплексными числами
Определение
1:
Системой комплексных чисел называется
множество
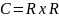 с операциями сложение и умножение:
с операциями сложение и умножение:
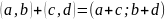 ;
;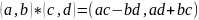 .
.
Теорема
1:
Система комплексных чисел
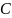 является полем.
является полем.
Док-во: 1 «+»: коммутативно
ассоциативно,
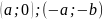 .
.
2 «*»:коммутативно
ассоциативно,
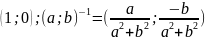 .
.
3 дистрибутивность □
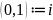 – называется
комплексной единицей.
– называется
комплексной единицей.
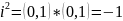 .
.
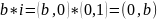 .
.
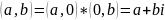 .
.
Определение:
Комплексное число
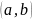 записанное в виде
записанное в виде
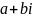 называется алгебраической формой
комплексного числа.
называется алгебраической формой
комплексного числа.
Утверждение 1: Сложение и умножение комплексных чисел в алгебраической форме:
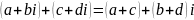 ;
;
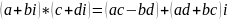 ;
;
Док-во:
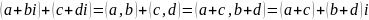 .
.
Аналогично для умножения.□
Замечание:
Пусть
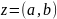 .
Поставим в соответствие числа на
декартовой плоскости с координатами
.
Поставим в соответствие числа на
декартовой плоскости с координатами
 .
Числу x
можно поставить в соответствие вектор
с началом в (0,0) и концом в
.
Длина этого вектора
.
Числу x
можно поставить в соответствие вектор
с началом в (0,0) и концом в
.
Длина этого вектора
 .
.
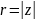
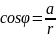 ,
,
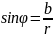 .
.
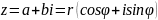 -
эта форма записи комплексного числа
называется тригонометрической.
-
эта форма записи комплексного числа
называется тригонометрической.
Утверждение 2:Умножение комплексных чисел в тригонометрической форме:
если
 ;
;
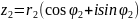 ,
то
,
то
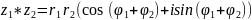 .
.
Утверждение
3:
Если
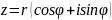 ,
,
 ,
то
,
то
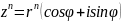 .
.
Определение:
Корнем n-ой
степени из комплексного числа z
называется такое число u,
что
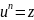 .
.
Обозначение:
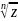 .
.
Теорема:
Пусть
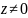 - комплексное число, тогда
ровно n
значений корня n-ой
степени из z
и они находятся по формуле:
- комплексное число, тогда
ровно n
значений корня n-ой
степени из z
и они находятся по формуле:
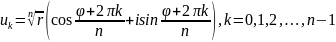 .
.
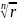 -
арифметическое значение корня.
-
арифметическое значение корня.
Следствие: Корни степени n из z находятся в вершинах правильного n-ка.
Следствие
2:
Множество
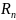 всех корней степени n
из 1 является мультипликативной группой.
всех корней степени n
из 1 является мультипликативной группой.
Док-во:
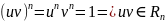
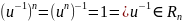
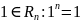 □
□
55. Определение кватернионов. Алгебраические операции над кватернионами. Тело кватернионов
Определение:
Алгеброй называется N-мерное векторное пространство над полем действительных чисел, если в нем однозначно определена и всегда выполняется операция умножения, ассоциативные, дистрибутивные относительно сложения и связанные с умножением элементов на действительные числа следующее равенств:
(kα)β=(αk)β=k(αβ), k ϵ R α, β ϵ A (A – алгебра)
Такая алгебра называется алгеброй ранга n.
Замечание: Алгебра является кольцом. Это кольцо не всегда коммутативно.
Определение: Если в алгебре ранга n выполнимо деление, то она называется телом (или алгеброй с делением ранга n).
Замечание: Тело может быть не коммутативным.
Алгебра
ранга n имеет некоторый базис
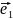 ,
,
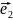 ,
…,
,
…,
 .
Элемент алгебры можно представить виде
α = (a1,
a2,
…,an).
.
Элемент алгебры можно представить виде
α = (a1,
a2,
…,an).
α = a1 +a2 +…+an
β = b1 +b2 +…+bn
Умножение
α∙β будет иметь вид
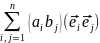 выражено через всевозможные комбинации
произведений базисных векторов.
выражено через всевозможные комбинации
произведений базисных векторов.
Пример алгебры:
Поле действительных чисел R можно рассматривать как одномерное векторное пространство с одним базисным вектором:
n=1  =1
=1
Любой элемент из R можно рассматривать как вектор α=α∙1. В этой алгебре выполнимо деление, поэтому R алгебра с делением ранга 1, причем коммутативная.
Поле комплексных чисел C:
n=2 =1, =i
Коммутативная алгебра с делением ранга.
Тело кватернионов H:
n=4
=1,
=i,
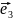 =j,
=j,
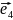 =k
=k
|
1 |
i |
j |
k |
1 |
1 |
i |
j |
k |
i |
i |
-1 |
k |
-j |
j |
j |
-k |
-1 |
i |
k |
k |
j |
-i |
-1 |
q1∙q2=(a1+b1i+c1j+d1k)(a2+b2i+c2j+d2k)=
=a1a2+a1b2i+a1c2j+a1d2k+
+b1ia2+b1ib2i+b1ic2j+b2id2k+
+c1ja2+c1jb2i+c1jc3j+c1jd2k+
+d1ka2+d1kb2i+d1kc3j+d1kd2k=
=(a1a2-b1b2-c1c2-d1d2)+(a1b2+b1a2-d1c2+c1d2)i+(a1c2-b1d2+c1a2+d1b2)j+(a1d2+b1c2-c1b2+d1a2)k
Замечание:
Умножение коммутативно и это легко проверить: (q1q2)q3=q1(q2q3)
Алгебра H – есть алгебра с делением, т.е. тело (не коммутативное поле). Для этого достаточно убедиться, что в H содержится единица и любой другой кватернион не равный 0имеет обратный:
q≠0 q-1: qq-1=q-1q=1
Определение:
Если
q=a+bi+cj+dk, то число
 =
a-bi-cj-dk называется сопряженным к числу
q.
=
a-bi-cj-dk называется сопряженным к числу
q.
Найдем
чему равно произведение
q∙
=
∙q=a2+b2+c2+d2=N(q).
N(q)
называется нормой q.
q≠0 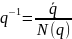
Замечание:
Нахождение частного от деления кватерниона q1 на q≠0 сводится к решению двух (умножение не коммутативно) уравнений:
x∙q=q1 – решается умножением обеих частей справа на q-1
q∙y=q1 – решается умножением обеих частей слева на q-1
Пример:
Найти x из уравнения x∙q=q1, если q=2+3i+j-5k, q1=4+i-2j+3k
=2-3i-j+5k
N(q)=22+32+12+(-5)2=39

x=q1∙q-1=(4+i-2j+3k)∙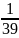 (2-3i-j+5k)=
(2-3i-j+5k)=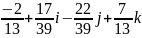
Вывод:
Алгебра кватернионов H есть алгебра с делением ранга 4 над полем действительных чисел (или тело).