- •1.Множество натуральных чисел n. Аксиомы Пеано
- •2.Независимость аксиом Пеано
- •3. Принцип полной математической индукции. Обобщенный принцип полной математической индукции. Примеры доказательства методом математической индукции
- •4. Сложение натуральных чисел как бинарная алгебраическая операция и как функция. Примеры. Свойство сокращения
- •5. Теорема о сложении натуральных чисел: единственность
- •6. Теорема о сложении натуральных чисел: существование
- •7.Ассоциативность сложения натуральных чисел
- •8. Коммутативность сложения натуральных чисел
- •Существование:
- •23. Частное натуральных чисел: определение и единственность. Свойства частного натуральных чисел
- •26. Свойства сложения и вычитания для натуральных чисел: .
- •27. Суммы и произведения нескольких натуральных чисел. Обобщенный закон дистрибутивности. Степень натурального числа с натуральным показателем и ее свойства
- •28. Равномощные множества. Отношение эквивалентности «быть равномощным». Отрезок натурального ряда. Конечные и бесконечные множества
- •29. Теорема о равномощности конечного множества только одному отрезку натурального ряда
- •30. Лемма о наибольшем и наименьшем элементе в конечном множестве. Бесконечность множества натуральных чисел
- •31. Счетность множеств целых и рациональных чисел. Несчетность множества действительных чисел
- •32. Отношение эквивалентности на множестве n2. Определение целого числа как класса эквивалентности на n2. Примеры
- •33. Определение суммы целых чисел и его корректность
- •34. Свойство сложения целых чисел
- •35. Определение произведения целых чисел и его корректность. Кольцо целых чисел и его свойства
- •38. Вложение множества натуральных чисел в кольцо целых чисел. Множество положительных целых чисел: определение, корректность определения, описание
- •40. Целое число как разность двух натуральных чисел. Отрицательные и положительные числа. Архимедовость и дискретность кольца целых чисел
- •41. Определение рациональных чисел как классов эквивалентности
- •42. Определение суммы рациональных чисел и его корректность. Аддитивная абелева группа рациональных чисел
- •43. Определение произведения рациональных чисел и его корректность. Поле рациональных чисел.
- •46. Вложение кольца целых чисел в поле рациональных чисел. Изоморфизм колец
- •47. Рациональное число как частное двух целых чисел. Поле рациональных как наименьшее поле, которое содержит кольцо целых чисел
- •49. Представление бесконечных периодических десятичных дробей обыкновенными дробями: правило, примеры
- •50. Определение действительных чисел как бесконечных десятичных дробей. Множество конечных десятичных дробей. Подходящие дроби
- •51. Определение и свойства отношения порядка на множестве действительных чисел
- •52. Плотность множества д в множестве действительных чисел
- •53. Определение и свойство суммы и произведения действительных чисел. Поле действительных чисел и его свойства
- •54. Определение, свойства и алгебраические операции с комплексными числами
- •55. Определение кватернионов. Алгебраические операции над кватернионами. Тело кватернионов
- •56. Вложение поля комплексных чиселв тело кватернионов. Теорема Фробениуса
1.Множество натуральных чисел n. Аксиомы Пеано
Числовая с-ма – числовое мн-во, на кот.заданы операции и отношения.
Сначало определяется аксиоматически с-ма нат.чисел. На ее основе строится с-ма целых чисел, а затем с-ма рац.чисел.
Мн-вом
нат.чисел
–
наз.непустое мн-во N
для эл-тов которых лпределено отношение
«непосредственно следует за»(число,кот.
непосредственно следует за a
обозн.
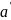 ),
т.е определено отношение,
кот.удовл.след.аксиомам:
),
т.е определено отношение,
кот.удовл.след.аксиомам:
А1: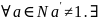 нат.число
единицы, кот.непосред. не следует ни за
каким нат.числом.
нат.число
единицы, кот.непосред. не следует ни за
каким нат.числом.
A2: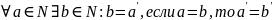 .Для
.Для
 нат.числа
нат.числа
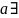 единств. нат.число
единств. нат.число
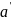 ,кот.непосредственно
следует за ним.
,кот.непосредственно
следует за ним.
A3: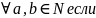
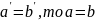 . Каждое
нат.число непоср. Следует не более чем
за одним нат.числом.
. Каждое
нат.число непоср. Следует не более чем
за одним нат.числом.
A4:(аксиома
индукции)
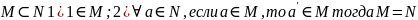
Мн-во М содержит все нат.числа.
Аксиомы А1-А4 наз. Аксиомами Пеано.
2.Независимость аксиом Пеано
А1: нат.число единицы, кот.непосред. не следует ни за каким нат.числом.
A2: .Для нат.числа единств. нат.число ,кот.непосредственно следует за ним.
A3: . Каждое нат.число непоср. Следует не более чем за одним нат.числом.
A4:(аксиома индукции)
Мн-во М содержит все нат.числа.
Аксиомы А1-А4 наз. Аксиомами Пеано.
Независимость А1 Независимость А2 Независимость А3 НезависимостьА4
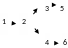
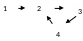
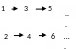
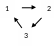
А1 не выполняется
3. Принцип полной математической индукции. Обобщенный принцип полной математической индукции. Примеры доказательства методом математической индукции
А1: нат.число единицы, кот.непосред. не следует ни за каким нат.числом.
A2: .Для нат.числа единств. нат.число ,кот.непосредственно следует за ним.
A3: . Каждое нат.число непоср. Следует не более чем за одним нат.числом.
A4:(аксиома индукции)
Мн-во М содержит все нат.числа.
Аксиомы А1-А4 наз. Аксиомами Пеано.
Замеч.Из акс.А4 следует законность док-в методом мат.индукции. При этом акс.инд.примен. в след.виде:
Теор.(принцип
полной мат.инд)
Утверждение T(n),
n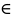 N
верно
N
верно
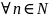 ,
если вып-ся след. условия:
,
если вып-ся след. условия:
1)Т(1)-истина; 2) : если T(n)-истина, то T(n’)-истина
Д-во:
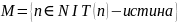
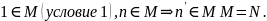
Замеч.Док-во на основ.принципа пол.мат.инд. наз. док-вом методом полной мат.инд. При этом говорят кратко докажем T(n) индукции по n. При этом: база инд: Т(1)-истина?
Предп.инд:
Т(n);
мат.инд: T(n)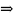 T(n’)
T(n’)
Пример.Д-ть
мнтодом полной мат.инд., что сумма n
первых нечетных нат.ч.=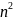 .
.
Решение: T(n): 1+3+5+..+(2n-1)=
T(1): 1=
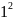 – истина;
2) T(n): 1+3+..+(2n-1)=
– истина;
2) T(n): 1+3+..+(2n-1)=
T(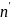 )=T(n+1)=1+3+..+(2n-1)+(2n+1)=
)=T(n+1)=1+3+..+(2n-1)+(2n+1)=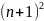
1+3+..+(2n-1)+(2n+1)=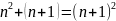
4. Сложение натуральных чисел как бинарная алгебраическая операция и как функция. Примеры. Свойство сокращения
Опр.1
Сложением на множестве натуральных
чисел называется бинарная алгебраическая
операция
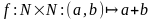 .
Она обозначается знаком «+» и результат
называется суммой которая удовлетворяет
следующим условиям:
.
Она обозначается знаком «+» и результат
называется суммой которая удовлетворяет
следующим условиям:
1)
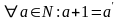 2)
2)
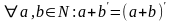
Пример: Найти сумму 2+5
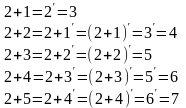
Опр.2
Сложением натуральных чисел называется
функция
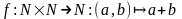 .
.
[a+b
называется суммой натуральных чисел a
и b
причем выполняются: 1)
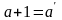 2)
2)
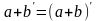 ]
]
При
фиксированном числе а
функция f
определяет функцию
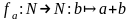 ,
которая удовлетворяет следующим условиям
,
которая удовлетворяет следующим условиям
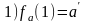 (
1)
(
1)
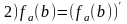 (2)
(2)
Теорема
(свойство сокращения)
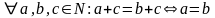
Доказательство: ММИ по (c)