Лекции по квантовой механике_1 / Lekciya4

Лекция 4

Матрицы операторов. Унитарные преобразования базиса. Соотношения коммутации. Одновременная измеримость физических величин. Соотношение неопределенностей Гейзенберга

Рассмотрим некоторый линейный оператор :. Выберем в рассматриваемом линейном пространстве дискретный ортонормированный базис. Так как каждому элементу этого пространства соответствует набор его координат в выбранном базисе, то оператору соответствует закон, связывающий координаты элементов линейного пространства. Можно доказать, что для любого линейного оператора закон, позволяющий найти координаты элемента по координатам элемента , можно представить в виде произведения некоторой матрицы из чисел на столбец, составленный из координат , , , … элемента

(1)

где под умножением матрицы на столбец понимается принятое в линейной алгебре правило матричного умножения («строка на столбец»):

(2)

Числа , которые являются характеристикой оператора, но не зависят от элемента , составляют матрицу оператора . Очевидно, размерность матрицы оператора совпадает с размерностью пространства, в котором оператор действует. В частности, операторам, действующим в бесконечномерных пространствах отвечают бесконечные матрицы.

Можно доказать, что сумме и произведению операторов отвечает сумма и произведение их матриц:

(3)

Матричные элементы матрицы оператора можно связать с результатом его действия на базисные элементы. Действительно, пусть - ортонормированный базис. Разложим элементы и в определении оператора по базису :

(4)

где - координаты элементов и . Умножим скалярно равенство (4) на и, пользуясь ортонормированностью базиса, линейностью оператора и скалярного произведения, получим

(5)

Сравнивая (4) с определением матрицы оператора, заключаем, что

(6)

Из формулы (6) можно получить ряд следствий.

1. Если в качестве базиса выбрать собственные функции оператора, его матрица является диагональной

(7)

причем на диагонали размещаются собственные значения оператора .

2. Матрицы сопряженных операторов транспонированы и комплексно сопряжены друг по отношению к другу:

(8)

3. При комплексном сопряжении и транспонировании матрицы эрмитова оператора получается та же матрица

если то (9)

4. При изменении базиса матрица изменяется. Остановимся на этом пункте более подробно. Пусть выбрано два ортонормированных базиса и . Каждый базисный элемент можно разложить по базису :

(10)

где - некоторые числа, которые образуют квадратную матрицу (удобнее выполнять суммирование по первому индексу матрицы - так, как это сделано в (10)). Матрицу принято называть матрицей перехода от одного базиса к другому. Очевидно, матрица перехода от одного ортонормированного базиса к другому является унитарной. Действительно, из ортонормированности обоих базисов имеем

(11)

Но так как , из (11) имеем

(12)

где - единичная матрица, что и означает, что матрица перехода унитарна (равенство (12) есть определение унитарного оператора).

Чтобы установить связь между матрицами одного и того же оператора при разных выборах базиса воспользуемся формулой (7) и формулой связи базисов

(13)

где и - матрицы оператора в базисе и соответственно. С помощью правил матричного умножения формулу (13) можно записать в виде

(14)

Из формулы (14), в частности, следует, что шпур матрицы оператора (сумма диагональных элементов) не зависит от выбора базиса или, как говорят, является инвариантным относительно выбора базиса (это связано с тем, что если под знак шпура входит произведение матриц, матрицы в нем можно циклически переставлять). Поэтому при любом выборе базиса шпур матрицы эрмитового оператора равен сумме его собственных значений. Также инвариантным является детерминант матрицы оператора.

Исследуем теперь вопрос о существовании общих собственных функций у разных операторов. Справедлива следующая

теорема:

Для того чтобы два оператора и имели полную систему общих собственных функций необходимо и достаточно, чтобы они коммутировали: .

Необходимость: Пусть - полная система общих собственных функций. Тогда любую функцию можно разложить по : . Подействуем на это равенство коммутатором

(15)

где собственные значения. Так как произвольна, то .

Достаточность: . Подействуем на уравнение на собственные функции оператора

(16)

где , - собственное значение и собственная функция оператора , оператором

(17)

Благодаря коммутации операторов и линейности оператора , имеем из (17)

(18)

Таким образом, функция также является собственной для оператора . Если у оператора невырожденный спектр, то собственному значению отвечает единственная собственная функция. Поэтому функция может отличаться от некоторым множителем:

(19)

где буквой обозначен указанный множитель. Уравнение (19) и означает, что функция является собственной и для оператора .

Если спектр оператора вырожден, то есть одному собственному значению отвечают несколько собственных функций, то функция , вообще говоря, не сводится к функции . В этом случае, однако, выбор собственных функций является неоднозначным и можно построить такие линейные комбинации собственных функций оператора , которые будут также и собственными для оператора . Теорема доказана.

Так как операторы координаты и импульса не коммутируют, они не имеют полной системы общих собственных функций. На самом деле у этих двух операторов нет ни одной общей собственной функции. Поэтому нет состояний, в которых и координата и импульс одновременно имели бы определенные значения (именно поэтому в квантовой механике нет понятия траектории). Всегда существует либо разброс координат, либо разброс импульсов, либо и то и другое. Рассмотрим утверждение, связывающее эти величины и которое является одним из основополагающим законов квантовой механики.

Соотношение неопределенностей Гейзенберга.

Исходя из коммутатора оператора координаты и импульса

(20)

докажем, что

т.е. неопределенности координаты и импульса не могут быть одновременно уменьшены до сколь угодно малых величин.

Для доказательства рассмотрим произвольное состояние . Пусть в этом состоянии: и (этого всегда можно добиться выбором системы координат). Тогда:

(21)

Рассмотрим некоторый функционал от действительной переменной :

(22)

Очевидно, что , как интеграл от четной неотрицательной функции. Учитывая, что x-действительная величина и что действие оператора координаты в собственном представлении сводится просто к умножению на значение координаты x, получим:

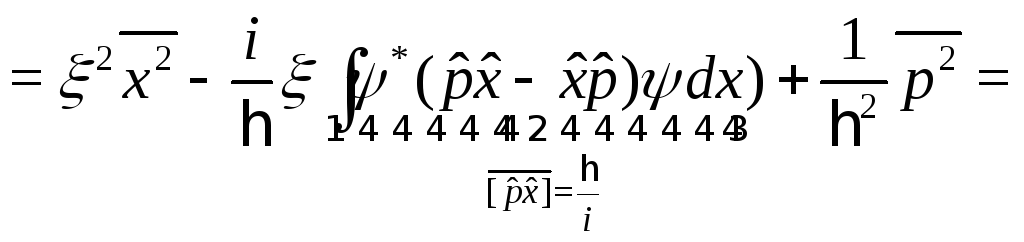
(23)

Полученное выражение как функция переменной , представляет собой параболу с ветвями, направленными вверх. Чтобы выполнялось неравенство (23) при любых необходимо, чтобы . Получим:

(24)

Или

Поскольку и , то:

Мы получили точную формулировку соотношения неопределенностей Гейзенберга.

Замечание:

1. Если бы операторы и коммутировали, то мы не смогли бы получить этого соотношения.

2. Состояние, которое «минимизирует» соотношение неопределенностей:

Это состояние представляет собой гауссовский волновой пакет. В нем:

6