Лекции по квантовой механике_1 / Lekciya18

Лекция 18

Спин 1/2. Спиновые функции, операторы спина. Матрицы Паули и их свойства. Разложение по спиновым функциям

Целый ряд элементарных частиц – электроны, нейтроны, протоны и другие – обладают спином . По этой причине рассмотрим подробно свойства спиновых функций и операторов именно в этом случае.

В этом случае проекция спина на ось может принимать два значения и , а потому спиновые волновые функции представляют собой двухкомпонентные спиноры

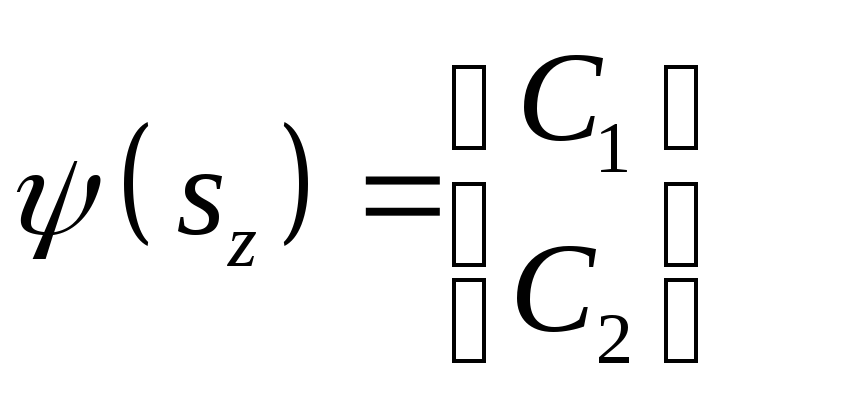(1)

причем вероятности различных значений проекции спина на ось равны

(2)

Построим матрицы спиновых операторов в -представлении. В этом представлении базисными функциями являются собственные функции оператора . Очевидно такими функциями являются следующие спиноры

(3)

Действительно, в состоянии проекция спина на ось принимает единственное значение , и, следовательно, эта функция – собственная для оператора , отвечающая собственному значению +1/2. Аналогично, функция - собственная функция оператора , отвечающая собственному значению -1/2.

Очевидно, искомые матрицы спиновых операторов представляют собой матрицы размерности . Начнем с построения матрицы оператора . Так как функции (3) – собственные функции оператора , то для искомой матрицы оператора выполнены следующие условия

(4)

Из формул (4) находим

(5)

Для построения матриц операторов и найдем сначала матрицы операторов . Поскольку коммутационные соотношения между операторами проекций спина такие же, как для операторов орбитального момента, то при действии операторов на собственные функции оператора получаются также собственные функции этого оператора, отвечающие на единицу большему или меньшему собственному значению. При действии операторов () на собственную функцию, отвечающую максимальному (минимальному) собственному значению получается спиновая функция, тождественно равная нулю, то есть нулевой столбец. Поэтому

(6)

Из соотношений (6) найдем, что

(7)

Из (7) и определения операторов находим

(8)

Матрицы операторов , и (5), (8) (без множителей 1/2) называются матрицами Паули и обозначаются , и .

Матрицу оператора легко найти, возводя в квадрат и складывая матрицы операторов проекций момента (5), (8)

(9)

Матрицу (9) можно было бы получить и по-другому из следующих рассуждений. Поскольку любая спиновая функция для частицы со спином 1/2 (то есть любой двумерный столбец) является собственной функцией оператора , отвечающей собственному значению (так как квадрат вектора спина такой частицы имеет в любом состоянии определенное значение), то матрица оператора является диагональной, причем диагональные матричные элементы равны , то есть матрица оператора и есть матрица (9).

Свойства матриц Паули

А. Все матрицы Паули, как матрицы операторов физических величин являются эрмитовыми.

Б. Для всех матриц Паули выполнено условие , где 1 – единичная матрица. Это можно проверить непосредственно. Это утверждение есть следствие того факта, что квадрат проекции спина частицы со спином ½ в любом состоянии имеет определенное значение (т.к. есть две возможности для проекции спина +1/2 и –1/2, а квадраты обоих этих чисел – ¼).

В.

Г. Любая матрица (22) может быть представлена в виде: . Это связано с тем, что единичная матрица и три матрицы Паули () образуют полный набор матриц (2), так как пространство таких матриц четырехмерно – матрица определяется заданием четырех чисел, поэтому любые четыре линейно независимые матрицы будут образовывать базис в пространстве таких матриц).

Д. . В частности, , т.е. они антикоммутируют. Алгебра (так называют правила умножения матриц) очень простая - при перестановке матриц просто меняется знак их произведения.

Е. Поскольку матрицы Паули связаны с операторами проекции спина 7на координатные оси для них выполнены обычные коммутационные соотношения для операторов проекций момента на координатные оси

(двойка в этом соотношении связана с тем, что ).

Рассмотрим теперь такой вопрос. Пусть частица находится в состоянии

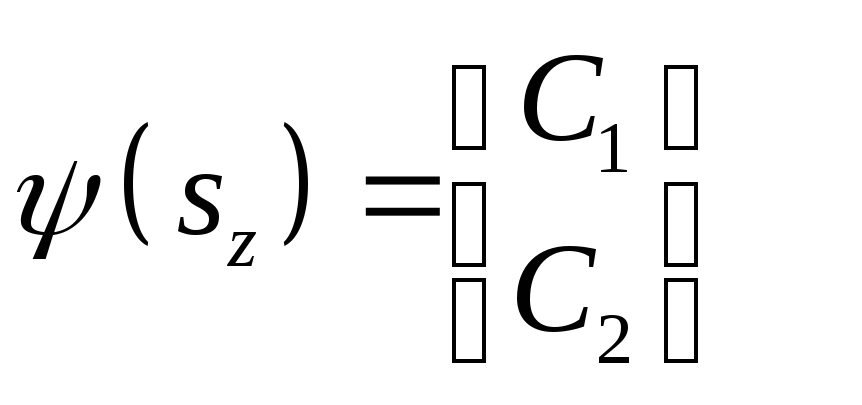(10)

Какие значения может принимать в этом состоянии проекция спина на ось и с какими вероятностями? Для ответа на этот вопрос необходимо найти собственные функции оператора и разложить по ним функцию (10).

Решаем уравнение

(11)

или

(12)

Система однородных алгебраических уравнений (12) имеет ненулевые решения в том случае, когда определитель этой системы равен нулю

(13)

Отсюда находим возможные значения проекций спина на ось (которые, как это и должно быть, равны возможным значениям проекции спина на ось ):

(14)

Подставляя теперь собственные значения (14) в систему уравнений (12), находим собственные функции

(15)

(множители возникли из условия нормировки).

Разложим теперь функцию (10) по собственным функциям (15). Это разложение имеет следующий вид

(16)

Отсюда согласно постулатам квантовой механики находим вероятности различных значений проекции спина на ось в состоянии (10):

(17)

Из формул (17), в частности, следует, что если частица находится в состоянии с определенной проекцией спина на ось ( или ), то вероятности различных значений проекции спина на ось одинаковы, что находится в соответствии с общим результатом, полученным ранее для собственных состояний операторов момента импульса в квантовой механике. В заключение отметим, что из формул (17) для вероятностей следует, что среднее значений проекции спина на ось равно

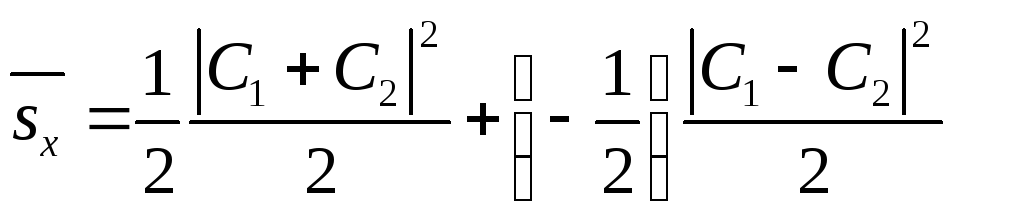(18)

Этот же результат можно получить, с использованеим квантовомеханической формулы для средних

(19)

где - спиновая функция (10), а матрица оператора определяется формулой (8).

5