17. Что называется главным квантовым числом

Целое число n в выражении (212.3), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n=1 является основным (нормальным) состоянием; состояния с n > 1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными

П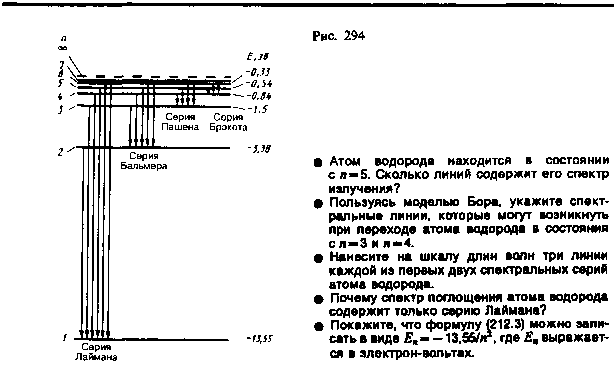 ридавая n различные целочисленные значения, получим для атома водорода (Z = 1), согласно формуле (212.3), возможные уровни энергии, схематически представленные на рис. 294. Энергия атома водорода с увеличением n возрастает и энергетические уровни сближаются к границе, соответствующей значению n = . Атом водорода обладает, таким образом, минимальной энергией (E₁ = –13,55 эВ) при n = 1 и максимальной (Е_ = 0) при n = . Следовательно, значение Е_ = 0 соответствует ионизации атома (отрыву от него электрона). Согласно второму постулату Бора , при переходе атома водорода (Z= 1) из стационарного состояния n в стационарное состояние т с меньшей энергией испускается квант

откуда частота излучения

где R = m_ee⁴/(8h³ )

Воспользовавшись при вычислении R современными значениями универсальных постоянных, получим величину, совпадающую с экспериментальным значением постоянной Ридберга в формулах для атома водорода . Это совпадение убедительно доказывает правильность полученной Бором формулы (212.3) для энергетических уровней водородоподобной систем

Подставляя, например, в формулу (212.4) т=1 и п=2, 3, 4, ..., получим группу линий, образующих серию Лаймана и соответствующих переходам электронов с возбужденных уровней (n = 2, 3, 4, ...) на основной (m = l)

Аналогично, при подстановке m = 2, 3, 4, 5, 6 и соответствующих им значений n получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представлена на рис. 294

. Следовательно, по теории Бора, количественно объяснившей спектр атома водорода, спектральные серии соответствуют излучению, возникающему в результате перехода атома в данное состояние из возбужденных состояний, расположенных выше данного

18.Корпускулярные и волновые характеристики и их связь

Французский ученый Луи де Бройль (1892—1987)выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами

С огласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия Е и импульс p, а с другой — волновые характеристики — частота  и длина волны . Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов (213.1)

1 9. Длина волны де Бройля

Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля 213.2 Это соотношение справедливо для любой частицы с импульсом р

Вскоре гипотеза де Бройля была подтверждена экспериментально. В 1927 г. американские физики К. Дэвиссон (1881—1958) и Л. Джермер (1896—1971) обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки — кристалла никеля, — дает отчетливую дифракционную картину

Так как дифракционная картина исследовалась для потока электронов, то необходимо было доказать, что волновые свойства присущи не только потоку большой совокупности электронов, но и каждому электрону в отдельности. Это удалось экспериментально подтвердить в 1948 г. российскому физику В. А. Фабриканту (р. 1907). Когда каждый электрон проходит через прибор, независимо от других, возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, для потоков электронов, в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой частице в отдельности

Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описывать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рассчитываемой по формуле де Бройля (213.2)

П редставление о двойственной корпускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы  и частотой  волн де Бройля (213.3)

Это свидетельствует о том, что соотношение между энергией и частотой в формуле (213.3) имеет характер универсального соотношения, справедливого как для фотонов, так и для любых других микрочастиц