13. Понятие относительных величин, величины планового задания, выполнения плана,динамики их взаимосвязь

Абсолютными величинами- наз-ся по-тели, кот характер-ют уровни, объемы изучаемых явл и процессов ( кг,дитры, шт)

Относительные величины- поктели, кот хар-ют колвенные соотн-я 2-х сопоставляемых величин. Она получается в рез-те деления абс величин.

Виды: 1. Относительная величина планового задания (показатель планового задания) представляет собой отношение планируемого уровня показателя к его уровню, достигнутому в предыдущем периоде (или в периоде, рассматриваемом как базисный).

Относительная величина планового задания характеризует перспективу развития явления

ОВПЗ = плановый уровень на будущий (следующий) период / фактический уровень текущего (предыдущего) периода

2. Относительная величина выполнения плана (показатель выполнения плана) характеризует степень реализации плана.

ОВВП = фактический уровень текущего периода / план текущего периода.

3. Относительная величина (показатель) динамики — характеризует изменение явления во времени. Бывает- базисные, цепные.

Взаимосвязь-(если они рассчитаны для одного периода времени): x =

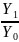
14.Относительные величины структуры, интенсивности,координации и сравения

4.структуры- характер-ет состав изучаемой совокуп-ти и показывает какую долю (удельный вес) составляет каждая часть в общем целом.

5. координации-хар-ет соотн-е частей целого, одна из кот принимается за базу сравнения

6.интенсивности- хар-ет степень распространения явл-я в определенной среде

7.сравнения-хар-ет соотн-е одноименных пок-телей, относящихся к различ объектам или территориям. При этом сравнимые пок-тели должны быть рассчитаны по одной методике

15.Понятие средних величин. Осн положения теории средних величин

Сред величины- пок-тели кот дают обобщенную хар-ку изучаемой совокуп-ти. Среднее включает то общее что есть в каждой единице совокп-ти(выбираются наиболее общие черты)

Статистич. Метод обработки данных методом средних величин заключается в замене индивидуал-х знач-й признака их средней. При этом общий объем изучаемой совокуп-ти должен оставаться постоянным.

Осн полож-я теории-1. Индивид знач-я из кот рассчит-ся средняя должны относится к однородной совокуп-ти и их число должно быть значительно

3.метод средних должен применятся вместе с методом группирвки, т.е необходимо предварительное распред-е совокуп-ти на однород группы.

3. наобходимость расчета групповых и общей средней для объективной и полной хар-ки изуч совокуп-ти

16. Средняя арифметическая простая и взвешенная. Расчет средней арифметической интервального ряда распределения.

Простая-применяется если каждое зн-е признака в ряде распред-я повторяется 1 или одинаковое кол-во раз

Взвешенная-если зн-е признака повтор-ся несколько раз

Расчет сред арифм интервального ряда- применяется формула средней арифм-ой взвешенной, в кот за X итое принимается середина каждого интервала При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.

Средние, вычисляемые из интервальных рядов являются приближенными.

17. Расчет средней из групповых средних и из относительных величин.

19.средняя гармоническая и простая взвешенная

20.сред геометриц и хронологич

Сред хронологич применяется если исходные данные представленны на опред даты, в момент времени

Сред геометрич-применяется для определени средних темпов роста в еденицу времени

21.средняя квадратическая. Взаимосвязь средних степенных величин.

-примен-ся для опред сред квадрата варианты.ф-лы:

Все простые степенные средние можно получить из след. Формулы:

Для одного ряда распред-я если значение признака варьируется между сред пок-телями имеет место зависимось:

Х сред.гармонич<х сред геометррич<х сред арифметич<х сред квадратич.

22.мода-варианта, кот имеет наиб частоту повторения в ряде распред-я. Для дискретных рядов распред-я мода опред-ся визуально по наибольшей величине. Для интервальных по формуле-

Модальным явл-ся интервал с наибольшей частотой

23.медиана-варианта кот делить ряды распред-я на 2 равных части. Для дискретных рядов-медиана-варианта. На кот приходятся полусумма накопленных частот или число несколько превышающее это значение.

медианный интервал-на кот приходится полусумма накопленных частот или число несколько превышающее из зн-е.