1.7. Мощность на валу рабочей машины

В ряде случаев необходимо знать характер изменения не только мо­мента, но и мощности на валу рабочей машины и электродвига­теля. Рассмотрим те же самые частные случаи (рис.1. 3).

1) х = 0.

Тогда Р = М_Н = а .

Значение мощности на валу рабочей машины изменяется

ли­нейно от частоты вращения.

2) х = 1. В этом случае Р_М = М = = К₁ .

Таким образом, мощность увеличивается пропорционально квадра­ту частоты вращения.

3) х = - 1.

Следовательно, с ростом частоты вращения мощность на валу рабочей машины остается постоянной.

3. х = 2.

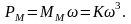
Мощность, потребляемая рабочей машиной, растет пропорционально кубу частоты вращения. Такая зависимость характерна для вентиляторов и центробежных насосов.

Следует отметить, что квадратичная зависимость момента и кубическая зависимость мощности от скорости справедливы при постоянстве КПД вентилятора или насоса. А это наблюдается при небольших изменениях частоты вращения. В случае существенного изменения частоты вращения эта зависимость нарушается и рост мощности, потребляемой рабочей машиной, будет несколько ниже.

У реальных машин зависимость Р = f( ) может иметь разнообразные виды, не поддающиеся аппроксимации. В тех случаях, когда механическая характеристика рабочей машины не подхо­дит к рассмотренным частным случаям, эту характеристику разбивают на несколько отрезков, на которых х будет равен 0; 1; -1; 2. Последовательно меняя х и пределы изменения частоты вращения, можно проводить аналитические исследования энергетики электро­привода.

Рис.1.3. Зависимость мощности рабочей машины от угловой скорости: 1 – вентилятора; 2 - зерновой нории ; 3 – конвейера;

4 – генератора постоянного тока.

Глава 2.

Электроприводы с двигателями постоянного тока

независимого и параллельного возбуждения

2.1. Электромеханическая и механическая характеристики

двигателя постоянного тока независимого

(параллельного) возбуждения

Из курса электрических машин известны следующие соотноше­ния между напряжением сети, ЭДС Е, частотой вращения , током I в установившемся режиме работы электрической машины:

U = E + Ir (2.1); E = cФ (2.2); r = r_я + R_доб (2.3)

где с - постоянный конструктивный коэффициент электрической машины; Ф - магнитный поток машины, Вб; - угловая частота вращения якоря двигателя, 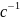; - сопротивление якорной цепи двигателя, Ом; R_доб - добавочное сопротивление.

Решив совместно уравнения (2.1...2.3), получим:

= Е/сФ = (U - IR)/сФ = /сФ - (r_я + R_доб)I/сФ. (2.4)

Выражение (2.4) называется электромеханической (или скоростной) характеристикой двигателя.

Если в процессе работы электрической машины значения напряжения, потока возбуждения и сопротивления остаются неизмен­ными, то

(2.5)

где - частота вращения идеального холостого хода двигателя при I = 0; _i - коэффициент жесткости электромеханической характе­ристики, = U/сФ;

_i = (r_я + R_доб)/cФ. (2.6)

Электромеханическая характеристика - это прямая линия 1, которая проходит через две точки (рис.2.1):

координаты первой точки: частота вращения равна нулю, ток равен пусковому .

координаты второй точки: ток равен нулю, частота вращения = _о. Из курса электрических машин известно, что значение элек­тромагнитного момента

М = сФI. (2.7)

Подставим значение тока из выражения (2.7) в (2.4):

= U/сФ - (r_я + R_доб)М/(сФ)². ( 2.8 )

Рис.2.1.Электромеханические - 1, 2 и механические – 3, 4 характеристики двигателя постоянного тока параллельного возбуждения.

Это выражение представляет механическую, характеристику двигателя. При постоянстве U, Ф_U и R_доб , уравнение (2.8) можно записать в виде

= _о - _МM. (2.9)

где _М - жесткость механической характеристики,

_М = ( r_я + R_доб)/(cФ)²

График механической характеристики 3 предста­влен на рис 2.1.

В области значительных нагрузок (I > I_H) в электрической машине начинает проявляться реакция якоря, и график 2 реальной электромеханической характеристики будет иной. При учете реакции якоря и механические харак­теристики двигателя несколько изменяются [4].

Механическая и электромеханическая характеристики являются естественными, если U = U_HДВ; R_доб = 0: Ф = Ф_НОМ . Их_. уравнения имеют следующий вид:

(2.10)

(2.11)

На практике необходимо знать характер изменения частоты вращения на валу от момента двигателя. График изменения частоты вращения и момента строят следующим образом [18]. Вначале определяют номина­льный момент на валу, соответствующий номинальной частоте вращения:

. (2.12)

Номинальный электромагнитный момент равен

(2.13)

Разность М_нэ и М_нв дает момент холостого хода. Этот мо­мент обусловлен потерями самого двигателя на перемагничивание стали якоря, вентиляцию и на трение в подшипниках:

М_хх = М_нэ - М_нв . (2.14)

Если подставим значение в выражение (2.11), получим частоту вращения холостого хода. При работе на естественной характеристике частота вращения двигателя обычно изменяется незначительно, следова­тельно, М_хх можно считать постоянным.

Рис.2.2. Зависимость угловой скорости двигателя постоянного тока независимого возбуждения от электромагнитного момента и

момента на его валу.

Соединив точки (М_нв и ) и (М = 0, и ), получим график изменения частоты вращения на валу двигателя от момента (рис.2.2). Для построения естественных электромеханической и механи­ческой характеристик двигателя постоянного тока независимого (параллельного) возбуждения необходимы

Р_H - номинальная мощность двигателя, кВт;

U_H - номинальное напряжение двигателя, В;

I_H - номинальный ток двигателя, А;

- номинальная частота вращения вала, .

Иногда в паспортных данных отсутствует значение номиналь­ного тока двигателя, дается номинальный КПД двигателя .

Для практических целей обычно строится не вся механическая характеристика, а часть, соответствующая изменению момента от нуля до М_ном (иногда до 2,5 М_ном) В этой части механическая характеристика линейна. Для ее построения достаточно двух точек с координатами:

При расчете координат этих точек последовательно опреде­ляем

1. номинальный КПД двигателя

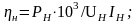(2.15)

если известен к.п.д., определяем ток:

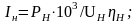
2. сопротивление якорной цепи

3. номинальную угловую частоту вращения

4. постоянный коэффициент

;

4. координаты первой точки

6) координаты второй точки

М_НЭ = сФ_HI_HM_НВ = Р_Н10³/ ;

7) момент холостого хода

М_ХХ = М_НЭ - М_НВ;

8) уравнение естественной характеристики для

электромаг­нитного момента

= U_Н/сФ_Н - Мr_Я/(сФ_н)².

Приравниваем М = М_ХХ и определяем

= U_Н/сФ_Н - r_{Я М} / (сФ_н)² М_В = 0

По данным пунктов 5 и б строим график = f(M_Э), а пунктов б и 9 - график = f(М_в) (рис.2.2). График = f(М_в) можно полу­чить сразу после построения = f(M_Э), не проводя вычислений по пунктам 7, 8, 9. Для этого необходимо отложить М при но­минальной частоте вращения и через полученную точку провести прямую, параллельную графику электромагнитного момента. Пересечение вновь построенной прямой с осью частоты вращения дает _ХХ.

При необходимости исследовать характер изменения момента двигателя на всем диапазоне изменения частоты вращения от нуля до 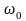, то координаты третьей точки:

; М_П = сФ_НU_H/r_{Я ;} I_П = U_H/r_Я

По полученным данным строят график механической

характе­ристики.