
- •Основы математического анализа
- •Часть I
- •Введение
- •Глава 1 элементы математической логики. §1. Высказывания. Логические операции над высказываниями.
- •§2. Правила вывода.
- •§3. Предикаты. Кванторы.
- •Глава 2 действительные числа Введение
- •§1. Сечения Дедекинда во множестве рациональных чисел.
- •§2. Действительные числа. Полнота множества действительных чисел.
- •§3. Числовые множества и их границы.
- •§4. Понятие об арифметических операциях над действительными числами.
- •§5. Модуль действительного числа и его свойства.
- •Глава 3 функции одной переменной. Предел функции. Непрерывность. §1. Понятие функции одной переменной. Обратная функция. Сложная функция.
- •§2. Элементарные функции. Свойства функций.
- •§3. Числовые последовательности.
- •§4. Понятие предела числовой последовательности.
- •§5. Основные теоремы о пределе последовательности.
- •§6. Бесконечно малые и бесконечно большие последовательности.
- •§7. Арифметические операции над пределами последовательностей.
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу .
- •§8. Неопределенности. Сравнение бесконечно малых последовательностей.
- •§9. Лемма о вложенных отрезках.
- •§10. Подпоследовательности. Частичные пределы.
- •§11. Число e.
- •§12. Предел функции.
- •§13. Основные теоремы о пределе функции.
- •§14. Односторонние пределы функции.
- •§15. Понятие непрерывности функции в точке. Арифметические операции над непрерывными функциями.
- •§16. Первый замечательный предел.
- •§17. Непрерывность элементарных функций.
- •§18. Некоторые пределы, связанные с показательной и логарифмической функциями.
- •§19. Односторонняя непрерывность. Классификация точек разрыва.
- •§20. Свойства функций, непрерывных на отрезке.
- •1 Теорема Вейерштрасса. Если функция определена и непрерывна на отрезке , то она ограничена.
- •2 Теорема Вейерштрасса. Если функция непрерывна на отрезке , то среди всех ее значений есть наибольшее и наименьшее.
- •1 Теорема Больцано-Коши. Если функция непрерывна на отрезке и на концах его принимает значения разных знаков, то внутри найдется точка такая, что .
- •2 Теорема Больцано-Коши. Если функция непрерывна на отрезке и , то для любого числа между и найдется точка из такая, что .
- •§21. Равномерная непрерывность функций.
§4. Понятие об арифметических операциях над действительными числами.
Пусть имеем два
действительных числа
и
.
Рассмотрим множество
всевозможных сумм рациональных чисел
 ,
где
,
где
 – рациональное число из
,
– рациональное число из
,
 – рациональное число из
,
а также множество
всевозможных сумм рациональных чисел
– рациональное число из
,
а также множество
всевозможных сумм рациональных чисел
 ,
где
,
где
 – рациональное число из
– рациональное число из
 ,
,
 – рациональное число из
– рациональное число из
 .
Легко видеть, что множество
ограничено сверху любой суммой
.
Следовательно, множество
имеет точную верхнюю грань
.
Легко видеть, что множество
ограничено сверху любой суммой
.
Следовательно, множество
имеет точную верхнюю грань
 ,
которую и назовем суммой действительных
чисел
,
которую и назовем суммой действительных
чисел
 и
и
 .
Можно убедиться, что при таком определении
сохраняются все свойства операции
сложения, имеющие место для рациональных
чисел.
.
Можно убедиться, что при таком определении
сохраняются все свойства операции
сложения, имеющие место для рациональных
чисел.
Определим теперь
произведение двух действительных чисел
и
.
Положим сначала, что
 и
и
 .
Рассмотрим множество
всевозможных произведений рациональных
чисел
.
Рассмотрим множество
всевозможных произведений рациональных
чисел
 ,
где
– рациональное число из
,
– рациональное число из
,
и множество Q2
всевозможных произведений рациональных
чисел
,
где
– рациональное число из
,
– рациональное число из
,
и множество Q2
всевозможных произведений рациональных
чисел
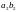 ,
где
-
рациональное число из
,
-
рациональное число из
.
Множество
ограничено сверху любым произведением
.
Следовательно,
имеет точную верхнюю грань
,
которую и назовем произведением
действительных чисел
,
где
-
рациональное число из
,
-
рациональное число из
.
Множество
ограничено сверху любым произведением
.
Следовательно,
имеет точную верхнюю грань
,
которую и назовем произведением
действительных чисел
 и
,
обозначая его символом
.
Если оба числа
и
отрицательны, то произведением чисел
и
назовем такое же число
,
которое получилось бы в результате
умножения двух положительных чисел
и
,
обозначая его символом
.
Если оба числа
и
отрицательны, то произведением чисел
и
назовем такое же число
,
которое получилось бы в результате
умножения двух положительных чисел
 и
и
 .
Если
.
Если
 ,
а
,
то их произведением называют число
,
а
,
то их произведением называют число
 .
Аналогично произведением чисел
и
в случае
.
Аналогично произведением чисел
и
в случае
 назовем число
назовем число
 .
.
Разность
действительных чисел
и
определим как сумму действительных
чисел
и
,
где
– есть произведение
 на
.
на
.
И, наконец, для
определения операции деления введем
понятие обратного числа для действительного
числа
 .
Ограничимся случаем иррационального
положительного
.
Предположим, что
определяется сечением
.
Ограничимся случаем иррационального
положительного
.
Предположим, что
определяется сечением
 во множестве
.
Обратным для
назовем число, обозначаемое
во множестве
.
Обратным для
назовем число, обозначаемое
 ,
которое определяется сечением (
,
которое определяется сечением ( ),
где к
),
где к
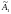 отнесем все отрицательные рациональные
числа, нуль и все числа вида
отнесем все отрицательные рациональные
числа, нуль и все числа вида
 ,
где
-
любое число из
.
К верхнему классу
,
где
-
любое число из
.
К верхнему классу
 отнесем все числа вида
отнесем все числа вида
 ,
где
– любое положительное число из
.
Отношением числа
к числу
назовем произведение
,
где
– любое положительное число из
.
Отношением числа
к числу
назовем произведение
 .
.
§5. Модуль действительного числа и его свойства.
Модулем, или
абсолютной величиной действительного
числа
(обозначение
 )
назовем само число
,
если оно неотрицательно и число
)
назовем само число
,
если оно неотрицательно и число
 ,
если
отрицательно. Таким образом,
,
если
отрицательно. Таким образом,
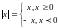 .
.
Рассмотрим свойства модуля.
1.  .
.
Это непосредственно следует из определения модуля.
2.  .
.
Действительно, из
определения модуля следует, что для
неотрицательного
это неравенство имеет вид
 ,
что очевидно; для отрицательного
имеем
,
что очевидно; для отрицательного
имеем
 ,
что также очевидно.
,
что также очевидно.
3. Неравенства
 и
и
 равносильны.
равносильны.
Пусть имеет место
неравенство
.
Из определения модуля следует, что это
неравенство равносильно системе:
 ,
которая равносильна системе
,
которая равносильна системе
 .
Если эту систему записать двойным
неравенством, то получим то, что
требовалось:
.
Теперь установим обратное, что выполнение
неравенства
влечет выполнение неравенства
.
В самом деле, запишем данное неравенство
в виде системы:
.
Если эту систему записать двойным
неравенством, то получим то, что
требовалось:
.
Теперь установим обратное, что выполнение
неравенства
влечет выполнение неравенства
.
В самом деле, запишем данное неравенство
в виде системы:
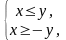 или
или

Но это и означает, что
.
4. 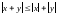
По свойству 2
рассмотрим два очевидных неравенства
и
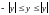 .
Сложив их, будем иметь
.
Сложив их, будем иметь
 .
Теперь, воспользовавшись свойством 3,
получим требуемое неравенство.
.
Теперь, воспользовавшись свойством 3,
получим требуемое неравенство.
5.  .
.
Представим
в виде

 и воспользуемся свойством 4.
и воспользуемся свойством 4.
 .
Если теперь перенести
.
Если теперь перенести
 из правой части в левую, то получим
требуемое неравенство.
из правой части в левую, то получим
требуемое неравенство.
