
- •Основы математического анализа
- •Часть I
- •Введение
- •Глава 1 элементы математической логики. §1. Высказывания. Логические операции над высказываниями.
- •§2. Правила вывода.
- •§3. Предикаты. Кванторы.
- •Глава 2 действительные числа Введение
- •§1. Сечения Дедекинда во множестве рациональных чисел.
- •§2. Действительные числа. Полнота множества действительных чисел.
- •§3. Числовые множества и их границы.
- •§4. Понятие об арифметических операциях над действительными числами.
- •§5. Модуль действительного числа и его свойства.
- •Глава 3 функции одной переменной. Предел функции. Непрерывность. §1. Понятие функции одной переменной. Обратная функция. Сложная функция.
- •§2. Элементарные функции. Свойства функций.
- •§3. Числовые последовательности.
- •§4. Понятие предела числовой последовательности.
- •§5. Основные теоремы о пределе последовательности.
- •§6. Бесконечно малые и бесконечно большие последовательности.
- •§7. Арифметические операции над пределами последовательностей.
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу .
- •§8. Неопределенности. Сравнение бесконечно малых последовательностей.
- •§9. Лемма о вложенных отрезках.
- •§10. Подпоследовательности. Частичные пределы.
- •§11. Число e.
- •§12. Предел функции.
- •§13. Основные теоремы о пределе функции.
- •§14. Односторонние пределы функции.
- •§15. Понятие непрерывности функции в точке. Арифметические операции над непрерывными функциями.
- •§16. Первый замечательный предел.
- •§17. Непрерывность элементарных функций.
- •§18. Некоторые пределы, связанные с показательной и логарифмической функциями.
- •§19. Односторонняя непрерывность. Классификация точек разрыва.
- •§20. Свойства функций, непрерывных на отрезке.
- •1 Теорема Вейерштрасса. Если функция определена и непрерывна на отрезке , то она ограничена.
- •2 Теорема Вейерштрасса. Если функция непрерывна на отрезке , то среди всех ее значений есть наибольшее и наименьшее.
- •1 Теорема Больцано-Коши. Если функция непрерывна на отрезке и на концах его принимает значения разных знаков, то внутри найдется точка такая, что .
- •2 Теорема Больцано-Коши. Если функция непрерывна на отрезке и , то для любого числа между и найдется точка из такая, что .
- •§21. Равномерная непрерывность функций.
§3. Числовые множества и их границы.
Числовым множеством будем называть любое множество, элементами которого являются действительные числа. Рассмотрим примеры числовых множеств.
Отрезок [a,b]. Это множество действительных чисел
 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
 .
.Интервал (a,b). Это множество действительных чисел , удовлетворяющих неравенству

b.
b.Полуинтервал (a,b]. Это множество действительных чисел , удовлетворяющих неравенству
 .
.
Определение
2.6. Числовое
множество
называют ограниченным сверху (снизу),
если найдется такое число
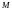 (число
(число
 ),
что для любого
из
выполняется неравенство
),
что для любого
из
выполняется неравенство
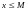 (
)
(
)
Число (число ) при этом называют верхней (нижней) гранью множества . В противном случае множество называют неограниченным сверху (снизу).
В символах
математической логики условие
ограниченности сверху множества
будет выглядеть так:
 .
.
Если множество
ограничено одновременно и сверху, и
снизу, то его называют просто ограниченным.
В символах математической логики условие
ограниченности множества X
запишется так:
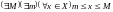 .
.
Тогда условие
неограниченности множества X
принимает вид
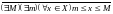 ,
или
,
или
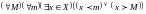 .
.
Легко видеть, что,
если множество ограничено сверху числом
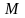 ,
то оно будет ограниченным сверху и любым
числом, большим, чем
.
Следовательно, ограниченное сверху
числовое множество имеет бесконечно
много верхних граней. Наибольший интерес
представляет наименьшая из всех верхних
граней. Она называется точной верхней
гранью множества. Аналогично, ограниченное
снизу числовое множество имеет бесконечно
много нижних граней, а наибольшая из
них называется точной нижней гранью.
Точная верхняя (нижняя) грань множества
обозначается символом
,
то оно будет ограниченным сверху и любым
числом, большим, чем
.
Следовательно, ограниченное сверху
числовое множество имеет бесконечно
много верхних граней. Наибольший интерес
представляет наименьшая из всех верхних
граней. Она называется точной верхней
гранью множества. Аналогично, ограниченное
снизу числовое множество имеет бесконечно
много нижних граней, а наибольшая из
них называется точной нижней гранью.
Точная верхняя (нижняя) грань множества
обозначается символом
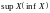 .
Рассмотрим примеры числовых множеств
и их границ.
.
Рассмотрим примеры числовых множеств
и их границ.
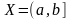 .
Это ограниченное множество :
.
Это ограниченное множество :
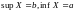 .
.
 .
Это ограниченное множество:
.
Это ограниченное множество:
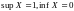 .
. .
(множество неотрицательных рациональных
чисел). Это множество не ограничено
сверху, но ограничено снизу, а,
следовательно, неограниченное.
.
(множество неотрицательных рациональных
чисел). Это множество не ограничено
сверху, но ограничено снизу, а,
следовательно, неограниченное.
ТЕОРЕМА 2.2. Всякое непустое ограниченное сверху числовое множество имеет точную верхнюю грань.
ДОКАЗАТЕЛЬСТВО. Пусть
-
непустое ограниченное сверху множество.
Очевидно, что, если в
есть наибольшее действительное число,
то это число и является точной верхней
гранью. Рассмотрим случай, когда в
нет наибольшего числа. Разобьем множество
всех действительных чисел
на два подмножества
и
так, что к
отнесем все верхние грани множества
,
а к
отнесем все остальные действительные
числа. Убедимся, что такое разбиение
является сечением Дедекинда. В самом
деле, оба множества
и
не пусты: в
имеется непустое множество
,
а в
имеется хотя бы одна верхняя грань для
,
так как
ограничено сверху. Любое действительное
число
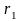 из
меньше любого действительного числа
из
меньше любого действительного числа
 из
.
Наконец, любое действительное число
лежит либо в
,
либо в
.
Значит
– сечение Дедекинда в
.
В силу полноты множества
пограничное число
между
и
является либо наибольшим в
,
либо наименьшим в
.
Но наибольшего в
нет по предположению. Следовательно,
является наименьшим числом в
,
т.е. точной верхней гранью множества
.
из
.
Наконец, любое действительное число
лежит либо в
,
либо в
.
Значит
– сечение Дедекинда в
.
В силу полноты множества
пограничное число
между
и
является либо наибольшим в
,
либо наименьшим в
.
Но наибольшего в
нет по предположению. Следовательно,
является наименьшим числом в
,
т.е. точной верхней гранью множества
.
ТЕОРЕМА 2.3. Всякое непустое ограниченное снизу числовое множествоимеет точную нижнюю грань.
ДОКАЗАТЕЛЬСТВО аналогично доказательству теоремы 2.2.
ТЕОРЕМА 2.4. Если
число
(число
)
является точной верхней (нижней) гранью
множества
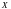 ,
то для любого числа
,
то для любого числа
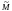 (числа
(числа
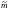 ),
меньшего
(большего
)
найдется такой элемент
),
меньшего
(большего
)
найдется такой элемент
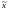 из
,
что
(
).
из
,
что
(
).
ДОКАЗАТЕЛЬСТВО. Пусть
 .
Выберем произвольно число
такое, что
.
Предположим, что в
не найдется такого элемента
,
который удовлетворял бы неравенству
.
Следовательно, для всех
из
выполняется неравенство
.
Это значит, что число
является верхней гранью для
.
Учитывая, что
,
должны иметь неравенство
,
которое
противоречит условию. Следовательно,
наше предположение неверно, и первая
часть теоремы доказана. Вторая часть
теоремы доказывается аналогично.
.
Выберем произвольно число
такое, что
.
Предположим, что в
не найдется такого элемента
,
который удовлетворял бы неравенству
.
Следовательно, для всех
из
выполняется неравенство
.
Это значит, что число
является верхней гранью для
.
Учитывая, что
,
должны иметь неравенство
,
которое
противоречит условию. Следовательно,
наше предположение неверно, и первая
часть теоремы доказана. Вторая часть
теоремы доказывается аналогично.
Суть рассмотренной теоремы состоит в том, что точные грани числового множества по сравнению с остальными гранями обладают особым свойством : к ним элементы множества могут подходить как угодно близко.
