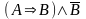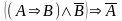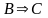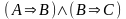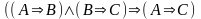§2. Правила вывода.

Среди различных сложных высказываний особое место занимают высказывания, которые являются истинными при любых значениях истинности входящих в них простых высказываний. Такие сложные высказывания называют правилами вывода. Рассмотрим некоторые из них.

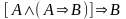1. (если , и из следует , то ).

По этой логической формуле построены многие математические доказательства. Составим таблицу истинности для этого высказывания, чтобы убедиться, что это есть правило вывода.

и	и	и	и	и
и	л	л	л	и
л	и	и	л	и
л	л	и	л	и

2. (если из следует , и не , то не ).

Таблица истинности для этого высказывания имеет вид

и	и	и	л	л	л	и
и	л	л	и	л	л	и
л	и	и	л	и	и	и
л	л	и	и	и	и	и

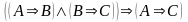3. (если из А следует В, и из В следует С, то из А следует С).

Это высказывание называется правилом силлогизма. Его таблица истинности имеет вид

и	и	и	и	и	и	и	и
и	и	л	и	л	л	л	и
и	л	и	л	и	л	и	и
и	л	л	л	и	л	л	и
л	и	и	и	и	и	и	и
л	и	л	и	л	л	и	и
л	л	и	и	и	и	и	и
л	л	л	и	и	и	и	и

§3. Предикаты. Кванторы.

В математике часто встречаются предложения, содержащие переменную. Например, рассмотрим предложение «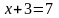 ». Это предложение не является высказыванием, поскольку мы не можем сказать, истинно оно или ложно, так как это зависит от . Если вместо подставить число 4, то получится истинное высказывание. Если вместо подставить любое другое число, то получится ложное высказывание. Если вместо подставить слово «дом», то получится бессмысленное высказывание. Такие бессмысленные высказывания условились считать ложными.

Определение 1.7. Предложения, в которые входят переменные и которые при замене этих переменных их значениями становятся высказываниями, называют предикатами.

Таким образом, предложение « » есть предикат. Предикат, содержащий одну переменную, называют одноместным, две переменные – двуместным и т.д. Предикаты, содержащие одну переменную , будем обозначать через или .

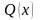Над предикатами можно выполнять такие же логические операции, как и над высказываниями.

Определение 1.8. Отрицанием предиката , определенного на множестве 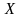, называется предикат 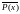(определенный на том же множестве ), значением которого для любого 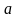из является отрицание 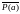высказывания .

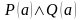Определение 1.9. Конъюнкцией предикатов и , имеющих общую область определения , называют предикат такой, что для любого из значением этого предиката является конъюнкция высказываний и .

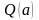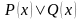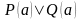Определение 1.10. Дизъюнкцией предикатов и , заданных на одном и том же множестве , называют предикат такой, что для любого значения из значением этого предиката является дизъюнкция высказываний и .

Определение 1.11. Импликацией предикатов и , заданных на одном и том же множестве , называется предикат 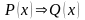такой, что для любого значения из значением этого предиката является импликация высказываний и .

Не следует думать, что всякое предложение, содержащее переменную, является предикатом. Например, предложение «для всех имеет место равенство » является высказыванием, и притом истинным высказыванием. Причина того, что предложение с переменной стало высказыванием заключена в словах «для всех », которыми связана переменная.

Сделаем обобщение. Пусть на множестве задан предикат . Тогда предложение «для всех 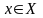истинно» является высказыванием и имеет специальное обозначение:

.

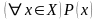Символ 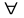называют квантором всеобщности, а присоединение его к предикату называют «навешиванием квантора на предикат».

Другим предложением с переменной, часто встречающимся в математике, является: «Во множестве Х существует такой элемент х, что Р(х) – истинно». Это предложение также является высказыванием и имеет специальное обозначение:

.

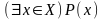Здесь символ называют квантором существования.

Обратим внимание на то, что операция «навешивания кванторов» применима только к предикатам и неприменима к высказываниям.

Рассмотрим некоторые наиболее важные преобразования предложений, содержащих кванторы.

Высказывание 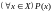можно рассматривать как множество высказываний P(a) для каждого а из Х, и каждое высказывание P(a) будет истинным. Но тогда будет истинной и конъюнкция этих высказываний. С другой стороны, истинность конъюнкции любого числа высказываний означает истинность каждого из высказываний, а, следовательно, можно записать

.

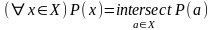Аналогично, высказывание можно рассматривать как множество высказываний P(a) для каждого а из Х, и среди этих высказываний найдется хотя бы одно истинное. Но тогда будет истинной дизъюнкция всех таких высказываний. С другой стороны, истинность дизъюнкции любого числа высказываний означает истинность хотя бы одного из них, т.е.

.

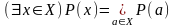Следовательно, учитывая законы де Моргана для бесконечного числа высказываний, получим

= = и .