- •Основы математического анализа
- •Часть I
- •Введение
- •Глава 1 элементы математической логики. §1. Высказывания. Логические операции над высказываниями.
- •§2. Правила вывода.
- •§3. Предикаты. Кванторы.
- •Глава 2 действительные числа Введение
- •§1. Сечения Дедекинда во множестве рациональных чисел.
- •§2. Действительные числа. Полнота множества действительных чисел.
- •§3. Числовые множества и их границы.
- •§4. Понятие об арифметических операциях над действительными числами.
- •§5. Модуль действительного числа и его свойства.
- •Глава 3 функции одной переменной. Предел функции. Непрерывность. §1. Понятие функции одной переменной. Обратная функция. Сложная функция.
- •§2. Элементарные функции. Свойства функций.
- •§3. Числовые последовательности.
- •§4. Понятие предела числовой последовательности.
- •§5. Основные теоремы о пределе последовательности.
- •§6. Бесконечно малые и бесконечно большие последовательности.
- •§7. Арифметические операции над пределами последовательностей.
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу .
- •§8. Неопределенности. Сравнение бесконечно малых последовательностей.
- •§9. Лемма о вложенных отрезках.
- •§10. Подпоследовательности. Частичные пределы.
- •§11. Число e.
- •§12. Предел функции.
- •§13. Основные теоремы о пределе функции.
- •§14. Односторонние пределы функции.
- •§15. Понятие непрерывности функции в точке. Арифметические операции над непрерывными функциями.
- •§16. Первый замечательный предел.
- •§17. Непрерывность элементарных функций.
- •§18. Некоторые пределы, связанные с показательной и логарифмической функциями.
- •§19. Односторонняя непрерывность. Классификация точек разрыва.
- •§20. Свойства функций, непрерывных на отрезке.
- •1 Теорема Вейерштрасса. Если функция определена и непрерывна на отрезке , то она ограничена.
- •2 Теорема Вейерштрасса. Если функция непрерывна на отрезке , то среди всех ее значений есть наибольшее и наименьшее.
- •1 Теорема Больцано-Коши. Если функция непрерывна на отрезке и на концах его принимает значения разных знаков, то внутри найдется точка такая, что .
- •2 Теорема Больцано-Коши. Если функция непрерывна на отрезке и , то для любого числа между и найдется точка из такая, что .
- •§21. Равномерная непрерывность функций.
Глава 1 элементы математической логики. §1. Высказывания. Логические операции над высказываниями.
Под высказыванием будем понимать всякое предложение, относительно которого можно сказать истинно оно или ложно. Рассмотрим примеры предложений, которые являются высказываниями или не являются ими.
Москва – столица России.
Который час?
Число 2 больше числа 3.
Все на выборы!
0,01 – малое число.
Треугольник, у которого все стороны равны, называют равносторонним.
Легко заметить, что восклицательные и вопросительные предложения высказываниями быть не могут. Поэтому предложения «Который час?» и «Все на выборы!» – не высказывания. Остальные четыре предложения – повествовательные. Однако высказываниями являются только предложения 1 и 3. Предложение 5 высказыванием не является, так как нет определения малого числа, а значит, мы не можем сказать истинно ли данное предложение. Предложение 6 представляет собой определение равностороннего треугольника. Поскольку суть математических определений состоит в присвоении терминов новым конструкциям, то ставить вопрос об истинности или ложности какого-либо определения бессмысленно. Это всего лишь соглашение. Следовательно, предложение 6 не является высказыванием.
Для обозначения истинности или ложности высказывания применяют буквенные обозначения: «и», «л» или цифровые: 1,0 соответственно. Мы будем использовать буквенные обозначения.
Простейшими логическими операциями, которые совершают над высказываниями, являются: отрицание, конъюнкция, дизъюнкция и импликация.
Определение
1.1. Отрицанием
высказывания
 называется высказывание
называется высказывание
 (читается «не
»),
которое ложно тогда, когда
истинно и истинно, когда
ложно.
(читается «не
»),
которое ложно тогда, когда
истинно и истинно, когда
ложно.
Для операции отрицания можно составить специальную таблицу, называемую таблицей истинности
|
и |
л |
|
л |
и |
Определение
1.2. Конъюнкцией
двух высказываний
и
 называют новое высказывание
называют новое высказывание
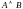 (читается «
и
»),
которое истинно, когда оба высказывания
и
истинны и ложно, когда хотя бы одно из
высказываний
и
ложно.
(читается «
и
»),
которое истинно, когда оба высказывания
и
истинны и ложно, когда хотя бы одно из
высказываний
и
ложно.
Таблица истинности для конъюнкции имеет вид
|
и |
и |
л |
л |
|
и |
л |
и |
л |
|
и |
л |
л |
л |
Определение
1.3. Дизъюнкцией
двух высказываний
и
называют новое высказывание
 (читается «
или
»),
которое истинно тогда, когда хотя бы
одно из высказываний
и
истинно и ложно, когда оба высказывания
и
ложны.
(читается «
или
»),
которое истинно тогда, когда хотя бы
одно из высказываний
и
истинно и ложно, когда оба высказывания
и
ложны.
Таблица истинности для дизъюнкции имеет вид
|
и |
и |
л |
л |
|
и |
л |
и |
л |
|
и |
и |
и |
л |
Если провести аналогию между операциями над множествами и логическими операциями над высказываниями, то заметим, что аналогом объединения множеств является дизъюнкция, аналогом пересечения множеств – конъюнкция.
Определение 1.4. Импликацией двух высказываний и называется такое высказывание А=>В (читается «из А следует В», или «если А, то В»), которое ложно тогда, когда А истинно, а В – ложно и истинно в остальных случаях.
Таблица истинности для импликации имеет вид
|
и |
и |
л |
л |
|
и |
л |
и |
л |
|
и |
л |
и |
и |
В результате логической операции над высказываниями получаются новые высказывания, над которыми, в свою очередь можно производить логические операции, получая более сложные высказывания. Если мы имеем простейшие высказывания А, В, С, D, то примерами сложных высказываний могут служить высказывания:
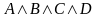 (конъюнкция четырех
высказываний)
(конъюнкция четырех
высказываний) (дизъюнкция четырех
высказываний)
(дизъюнкция четырех
высказываний)[(А=>В) C] =>
 (если из А следует В и С, то не D).
(если из А следует В и С, то не D).
Определение 1.5. Два высказывания называют равносильными, если они принимают одинаковые значения истинности при любых значениях истинности входящих в них высказываний.
Равносильность обозначается символом =.
Рассмотрим примеры равносильных высказываний.
закон двойного отрицания: =
 .
.
Действительно, составляя таблицы истинности, получаем
|
|
|
и |
л |
и |
л |
и |
л |
законы Де Моргана:
 ;
;
 .
.
Убедимся в справедливости этих формул, составив таблицы истинности.
|
|
|
|
|
|
|
|
|
|
и |
и |
л |
л |
и |
л |
л |
и |
л |
л |
и |
л |
л |
и |
л |
и |
и |
и |
л |
л |
л |
и |
и |
л |
л |
и |
и |
и |
л |
л |
л |
л |
и |
и |
л |
и |
и |
л |
и |
и |
Убедитесь
самостоятельно в справедливости законов
Де Моргана для трех высказываний:
 и
и
 ,
составив таблицы истинности.
,
составив таблицы истинности.
Важно заметить,
что законы Де Моргана можно
распространить на любое конечное и даже
бесконечное число высказываний. Если
для конъюнкции
 высказываний использовать символ
высказываний использовать символ
 ,
а для дизъюнкции – символ
,
а для дизъюнкции – символ
 ,
то законы де Моргана для
и бесконечного числа высказываний
принимают вид:
,
то законы де Моргана для
и бесконечного числа высказываний
принимают вид:
 ;
;  ;
;  ;
; 
В математике
большинство теорем имеет структуру
импликации
.
Если при этом теорему
назвать прямой, то утверждение
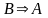 называют обратной теоремой; утверждение
=>
называют обратной теоремой; утверждение
=> называют противоположной теоремой, а
утверждение
называют противоположной теоремой, а
утверждение
 =>
называют противоположной обратной
теоремой.
=>
называют противоположной обратной
теоремой.
Рассмотрим пример. Пусть имеем теорему «Если треугольник АВС равнобедренный, то углы при основании равны». Обратной теоремой будет утверждение «Если углы при основании треугольника АВС равны, то треугольник – равнобедренный». Противоположная теорема формулируется в виде «Если треугольник АВС не равнобедренный, то углы при основании не равны». И, наконец, противоположная обратной теорема имеет формулировку «Если углы при основании треугольника АВС не равны, то треугольник – не равнобедренный».
Определение 1.6. Если импликация является истинной, то высказывание называют необходимым условием для , а высказывание называют достаточным условием для высказывания .
Наибольший интерес в математике представляет условие, которое является одновременно необходимым и достаточным. Из определения 1.6 следует, что условие является необходимым и достаточным для условия , если одновременно истинны импликации и . Составим таблицу истинности для этих импликаций и выясним, когда это возможно.
|
|
|
|
и |
и |
и |
и |
и |
л |
л |
и |
л |
и |
и |
л |
л |
л |
и |
и |
Из таблицы видно, что обе импликации истинны в двух случаях, когда высказывания и оба истинны или оба ложны (см. первую и последнюю строки таблицы), то есть равносильны. Таким образом, если условие является необходимым и достаточным для условия , то это означает равносильность этих высказываний и . Кроме закона двойного отрицания и законов де Моргана, рассмотренных ранее, большое значение имеют следующие равносильности.
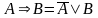 .
.
Проверим справедливость равенства, составив таблицу истинности
|
|
|
|
|
и |
и |
и |
л |
и |
и |
л |
л |
л |
л |
л |
и |
и |
и |
и |
л |
л |
и |
и |
и |
( ) = (
 ).
).
Записанная логическая формула утверждает равносильность прямой и противоположной обратной теорем. Убедиться в этом можно с помощью таблицы истинности
|
|
|
|
|
|
и |
и |
и |
л |
л |
и |
и |
л |
л |
и |
л |
л |
л |
и |
и |
л |
и |
и |
л |
л |
и |
и |
и |
и |
( ) = [
 ].
].
Это логическая формула метода доказательства от противного. Убедиться в ее справедливости можно составив таблицу истинности.
|
|
|
|
|
|
|
и |
и |
и |
л |
л |
л |
и |
и |
л |
л |
и |
л |
и |
л |
л |
и |
и |
л |
и |
л |
и |
л |
л |
и |
и |
и |
л |
и |