
- •Основы математического анализа
- •Часть I
- •Введение
- •Глава 1 элементы математической логики. §1. Высказывания. Логические операции над высказываниями.
- •§2. Правила вывода.
- •§3. Предикаты. Кванторы.
- •Глава 2 действительные числа Введение
- •§1. Сечения Дедекинда во множестве рациональных чисел.
- •§2. Действительные числа. Полнота множества действительных чисел.
- •§3. Числовые множества и их границы.
- •§4. Понятие об арифметических операциях над действительными числами.
- •§5. Модуль действительного числа и его свойства.
- •Глава 3 функции одной переменной. Предел функции. Непрерывность. §1. Понятие функции одной переменной. Обратная функция. Сложная функция.
- •§2. Элементарные функции. Свойства функций.
- •§3. Числовые последовательности.
- •§4. Понятие предела числовой последовательности.
- •§5. Основные теоремы о пределе последовательности.
- •§6. Бесконечно малые и бесконечно большие последовательности.
- •§7. Арифметические операции над пределами последовательностей.
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу .
- •§8. Неопределенности. Сравнение бесконечно малых последовательностей.
- •§9. Лемма о вложенных отрезках.
- •§10. Подпоследовательности. Частичные пределы.
- •§11. Число e.
- •§12. Предел функции.
- •§13. Основные теоремы о пределе функции.
- •§14. Односторонние пределы функции.
- •§15. Понятие непрерывности функции в точке. Арифметические операции над непрерывными функциями.
- •§16. Первый замечательный предел.
- •§17. Непрерывность элементарных функций.
- •§18. Некоторые пределы, связанные с показательной и логарифмической функциями.
- •§19. Односторонняя непрерывность. Классификация точек разрыва.
- •§20. Свойства функций, непрерывных на отрезке.
- •1 Теорема Вейерштрасса. Если функция определена и непрерывна на отрезке , то она ограничена.
- •2 Теорема Вейерштрасса. Если функция непрерывна на отрезке , то среди всех ее значений есть наибольшее и наименьшее.
- •1 Теорема Больцано-Коши. Если функция непрерывна на отрезке и на концах его принимает значения разных знаков, то внутри найдется точка такая, что .
- •2 Теорема Больцано-Коши. Если функция непрерывна на отрезке и , то для любого числа между и найдется точка из такая, что .
- •§21. Равномерная непрерывность функций.
§17. Непрерывность элементарных функций.
Покажем сначала, что основные элементарные функции непрерывны в любой точке своей области определения.
Непрерывность функции
 была установлена в § 16.
была установлена в § 16.
Доказательство непрерывности функции
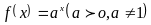 в произвольной точке
из области определения проведем в два
этапа. Сначала покажем непрерывность
этой функции в точке
в произвольной точке
из области определения проведем в два
этапа. Сначала покажем непрерывность
этой функции в точке
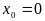 ,
т.е. что
,
т.е. что
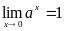 .
Рассмотрим два случая, когда
.
Рассмотрим два случая, когда
 и когда
и когда
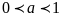 .
.
Пусть
.
Зададим произвольно
 и найдем
такое, что при всех
,
удовлетворяющих неравенству
и найдем
такое, что при всех
,
удовлетворяющих неравенству
 ,
будет выполняться условие
,
будет выполняться условие
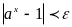 .
Рассмотрим неравенство
.
Оно равносильно неравенству
.
Рассмотрим неравенство
.
Оно равносильно неравенству
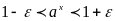 ,
которое равносильно неравенству
,
которое равносильно неравенству
 .
Выберем наименьшее из чисел
.
Выберем наименьшее из чисел
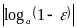 и
и
 .
Так как
.
Так как

 ,
,
то > . Поэтому, взяв в качестве любое положительное число, меньшее чем , при всех , удовлетворяющих условию , будет обеспечено выполнение неравенства .
Пусть теперь
.
Тогда рассмотрим число
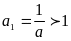 .
Для числа
.
Для числа
 было установлено, что
было установлено, что
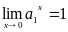 .
Значит
.
Значит
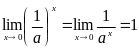 .
Отсюда получаем
.
.
Отсюда получаем
.
Теперь покажем, что показательная функция непрерывна в любой точке из области определения.
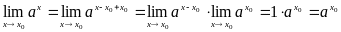 ,
,
что и требовалось доказать.
Установим теперь непрерывность функции
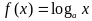 в точке
из области определения, т.е. покажем,
что
в точке
из области определения, т.е. покажем,
что
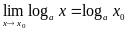 .
.
Зададим произвольно и найдем такое, что
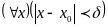
 .
.
Неравенство
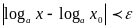 равносильно неравенству
равносильно неравенству
 ,
которое равносильно совокупности
,
которое равносильно совокупности
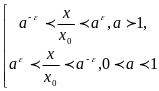
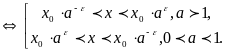
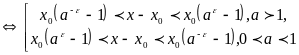 .
.
Для каждого случая
находим
как положительное число, меньшее чем
 .
.
Покажем непрерывность
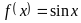 в произвольной точке
.
Зададим произвольно
и найдем
такое, что при всех
,
удовлетворяющих неравенству
в произвольной точке
.
Зададим произвольно
и найдем
такое, что при всех
,
удовлетворяющих неравенству
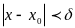 ,
выполняется условие
,
выполняется условие
 .
.
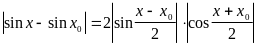 .
.
Поскольку
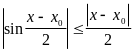 ,
а
,
а
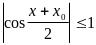 ,
то
,
то
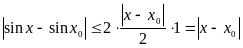 .
.
Отсюда приходим
к выводу, что, в качестве
можно взять любое положительное число,
меньшее
.
Совершенно аналогично можно установить
непрерывность функции
в любой точке
,
т.е. справедливость равенства
 .
.
После этого на
основании теоремы 3.26 можно утверждать,
что в любой точке области определения
будут непрерывны функции
 и
и
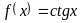 .
.
У
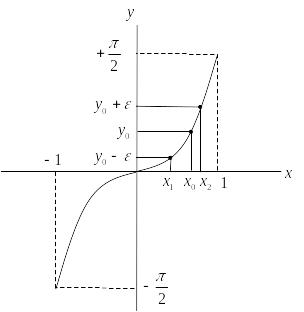 становим
теперь непрерывность функции
становим
теперь непрерывность функции
 в произвольной точке
из области определения. Известно, что
функция
на отрезке
в произвольной точке
из области определения. Известно, что
функция
на отрезке
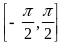 монотонно возрастает от -1 до +1. Поэтому
функция
устанавливает взаимно-однозначное
соответствие между отрезками
и
монотонно возрастает от -1 до +1. Поэтому
функция
устанавливает взаимно-однозначное
соответствие между отрезками
и
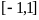 .
Этот факт позволяет определить на
[-1,1] функцию
,
обратную к функции.
.
Функция
,
как и функция
,
будет монотонно возрастающей. Возьмем
произвольную точку
из
.
Ей будет соответствовать точка
.
Этот факт позволяет определить на
[-1,1] функцию
,
обратную к функции.
.
Функция
,
как и функция
,
будет монотонно возрастающей. Возьмем
произвольную точку
из
.
Ей будет соответствовать точка
 из
.
Зададим произвольно
так, чтобы точки
из
.
Зададим произвольно
так, чтобы точки
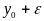 и
и
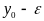 лежали на отрезке
.
Покажем, как можно найти
такое, чтобы при всех
,
удовлетворяющих неравенству
,
выполнялось условие
лежали на отрезке
.
Покажем, как можно найти
такое, чтобы при всех
,
удовлетворяющих неравенству
,
выполнялось условие
 .
.
Для числа
найдется такое
из [-1,1] ,что
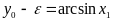 .
Аналогично для числа
найдется число
.
Аналогично для числа
найдется число
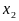 из [-1,1] такое, что
из [-1,1] такое, что
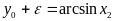 .
При этом в силу монотонного возрастания
функции
из того, что
.
При этом в силу монотонного возрастания
функции
из того, что
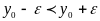 будем иметь:
будем иметь:
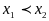 (см. рисунок). Отсюда видно, что в качестве
можно взять любое положительное число
меньшее, чем
(см. рисунок). Отсюда видно, что в качестве
можно взять любое положительное число
меньшее, чем
 .
.
Замечание. Если
же
будет таким, что
 выйдет за пределы отрезка [-1,1], то в
качестве
выйдет за пределы отрезка [-1,1], то в
качестве
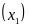 можно взять число 1 (число -1).
можно взять число 1 (число -1).
Если учесть, что
 ,
то функция
,
то функция
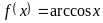 непрерывна в любой точке из области
определения по теореме 3.26.
непрерывна в любой точке из области
определения по теореме 3.26.
Непрерывность
функций
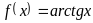 и
и
 в любой точке области определения
устанавливается аналогично непрерывности
.
в любой точке области определения
устанавливается аналогично непрерывности
.
Для установления непрерывности степенной функции докажем предварительно теорему о непрерывности сложной функции.
ТЕОРЕМА 3.28. Пусть
имеем сложную функцию
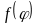 .
Если функция
.
Если функция
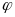 непрерывна в точке
,
а функция
непрерывна в точке
непрерывна в точке
,
а функция
непрерывна в точке
 ,
то сложная функция
непрерывна в точке
.
,
то сложная функция
непрерывна в точке
.
ДОКАЗАТЕЛЬСТВО. Зададим
произвольно
и найдем для него в силу непрерывности
функции
в точке
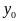 такое
,
что при всех
такое
,
что при всех
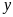 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
 ,
выполняется условие
,
выполняется условие
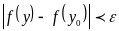 .
Далее, для найденного
силу непрерывности функции
в точке
найдется
.
Далее, для найденного
силу непрерывности функции
в точке
найдется
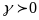 ,
такое, что при всех
,
удовлетворяющих неравенству
,
такое, что при всех
,
удовлетворяющих неравенству
 ,
выполняется условие
,
выполняется условие
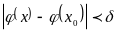 .
Таким образом, для произвольно заданного
находится
такое, что при всех
,
удовлетворяющих неравенству
,
выполняется условие
,
которое влечет за собой выполнение
условия
.
Таким образом, для произвольно заданного
находится
такое, что при всех
,
удовлетворяющих неравенству
,
выполняется условие
,
которое влечет за собой выполнение
условия
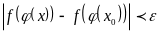 ,
что и означает непрерывность функции
в точке
.
,
что и означает непрерывность функции
в точке
.
Теперь покажем, что функция
 непрерывна в произвольной точке
.
Запишем данную функцию в виде
непрерывна в произвольной точке
.
Запишем данную функцию в виде
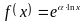 .
Функция
.
Функция
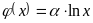 непрерывна в любой точке
из области определения. Функция
непрерывна в любой точке
из области определения. Функция
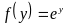 непрерывна в любой точке
из области определения. Следовательно,
по теореме 3.28 будет непрерывной в точке
и сложная функция
непрерывна в любой точке
из области определения. Следовательно,
по теореме 3.28 будет непрерывной в точке
и сложная функция
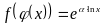 .
.
Опираясь на теоремы 3.26 и 3.28 можно утверждать, что любая элементарная функция будет непрерывной в своей области определения.
