§13. Основные теоремы о пределе функции.

ТЕОРЕМА 3.14. Если функция имеет предел в точке , то он единственный.

ДОКАЗАТЕЛЬСТВО. Пусть . Возьмем произвольную последовательность , сходящуюся к . Тогда по определению 3.17 последовательность должна сходиться к числу . А так как сходящаяся последовательность имеет единственный предел, то теорема доказана.

ТЕОРЕМА 3.15. Функция , имеющая предел в точке , ограничена в некоторой окрестности точки .

ТЕОРЕМА 3.16. Если , и в проколотой окрестности точки выполняется неравенство , то .

ТЕОРЕМА 3.17. Если , и в проколотой окрестности точки выполняется неравенство , то .

ДОКАЗАТЕЛЬСТВА теорем 3.15, 3.16, 3.17 непосредственно вытекают из соответственных теорем для пределов последовательности и определения предела функции в точке по Гейне.

ТЕОРЕМА 3.18. Если и , то в некоторой проколотой окрестности точки выполняется неравенство .

ДОКАЗАТЕЛЬСТВО. Пусть для определенности . Зададим и найдем такое, что при всех , удовлетворяющих условию , выполняется неравенство , или, . Отсюда получаем

.

Далее, опираясь на определение 3.17, можно перенести все теоремы о пределе последовательности на предел функции действительного аргумента.

Определение 3.18. Функцию называют бесконечно малой в точке , если .

ТЕОРЕМА 3.19. Чтобы функция имела пределом число в точке , необходимо и достаточно чтобы функция была бесконечно малой в точке .

ТЕОРЕМА 3.20. Если и – бесконечно малые функции в точке , то – тоже бесконечно малая функция в точке .

Следствие Сумма конечного числа бесконечно малых функций в точке есть бесконечно малая функция в этой точке.

ТЕОРЕМА 3.21. Если – бесконечно малая функция в точке , а – ограниченная функция в проколотой окрестности точки , то – есть бесконечно малая функция в точке .

Следствие 1 Если – бесконечно малая функция в точке , то – тоже есть бесконечно малая функция в точке , где - некоторое действительное число.

Следствие 2 Произведение конечного числа бесконечно малых функций в точке есть бесконечно малая функция в точке .

Определение 3.19. Функцию называют бесконечно большой в точке , если

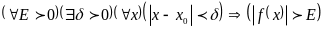
ТЕОРЕМА 3.22. Чтобы функция была бесконечно большой в точке , необходимо и достаточно чтобы в точке функция была бесконечно малой.

ТЕОРЕМА 3.23. Если , , то ,

ТЕОРЕМА 3.24. Если , , причем , то .

Для функций действительного аргумента можно говорить о неопределенностях таких же видов, что и для последовательностей.

§14. Односторонние пределы функции.

При определении предела функции в точке ничего не говорилось о том, как аргумент приближается к . Он может приближаться к монотонно возрастая, т.е. слева от ; монотонно убывая, т.е. справа от или немонотонно. Желая подчеркнуть, как именно аргумент приближается к , вводят понятие одностороннего предела функции.

Определение 3.20. Число называют пределом справа (слева) функции в точке , если

Обозначение: .

Пределы справа и слева называют односторонними пределами функции.

ТЕОРЕМА 3.25. Чтобы функция имела предел в точке , необходимо и достаточно чтобы она имела в этой точке оба односторонних предела и чтобы они были равны.

ДОКАЗАТЕЛЬСТВО. Необходимость очевидна. Докажем достаточность. Пусть функция имеет оба односторонних предела в точке и они равны числу . Зададим произвольно . Для этого из того, что найдем такое, что при всех , удовлетворяющих неравенству , выполняется условие . Для того же из того, что находим такое, что при всех , удовлетворяющих неравенству , выполняется условие . Пусть теперь . Тогда , а это и означает, что .

Теорема доказана.