
- •Основы математического анализа
- •Часть I
- •Введение
- •Глава 1 элементы математической логики. §1. Высказывания. Логические операции над высказываниями.
- •§2. Правила вывода.
- •§3. Предикаты. Кванторы.
- •Глава 2 действительные числа Введение
- •§1. Сечения Дедекинда во множестве рациональных чисел.
- •§2. Действительные числа. Полнота множества действительных чисел.
- •§3. Числовые множества и их границы.
- •§4. Понятие об арифметических операциях над действительными числами.
- •§5. Модуль действительного числа и его свойства.
- •Глава 3 функции одной переменной. Предел функции. Непрерывность. §1. Понятие функции одной переменной. Обратная функция. Сложная функция.
- •§2. Элементарные функции. Свойства функций.
- •§3. Числовые последовательности.
- •§4. Понятие предела числовой последовательности.
- •§5. Основные теоремы о пределе последовательности.
- •§6. Бесконечно малые и бесконечно большие последовательности.
- •§7. Арифметические операции над пределами последовательностей.
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу ;
- •Последовательность сходится к числу .
- •§8. Неопределенности. Сравнение бесконечно малых последовательностей.
- •§9. Лемма о вложенных отрезках.
- •§10. Подпоследовательности. Частичные пределы.
- •§11. Число e.
- •§12. Предел функции.
- •§13. Основные теоремы о пределе функции.
- •§14. Односторонние пределы функции.
- •§15. Понятие непрерывности функции в точке. Арифметические операции над непрерывными функциями.
- •§16. Первый замечательный предел.
- •§17. Непрерывность элементарных функций.
- •§18. Некоторые пределы, связанные с показательной и логарифмической функциями.
- •§19. Односторонняя непрерывность. Классификация точек разрыва.
- •§20. Свойства функций, непрерывных на отрезке.
- •1 Теорема Вейерштрасса. Если функция определена и непрерывна на отрезке , то она ограничена.
- •2 Теорема Вейерштрасса. Если функция непрерывна на отрезке , то среди всех ее значений есть наибольшее и наименьшее.
- •1 Теорема Больцано-Коши. Если функция непрерывна на отрезке и на концах его принимает значения разных знаков, то внутри найдется точка такая, что .
- •2 Теорема Больцано-Коши. Если функция непрерывна на отрезке и , то для любого числа между и найдется точка из такая, что .
- •§21. Равномерная непрерывность функций.
§6. Бесконечно малые и бесконечно большие последовательности.
Определение
3.12. Последовательность
 называют бесконечно малой, если
называют бесконечно малой, если
 (т.е. если
(т.е. если
 ).
).
ТЕОРЕМА 3.6. Чтобы
последовательность
сходилась к числу
,
необходимо и достаточно чтобы
последовательность
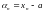 была бесконечно малой.
была бесконечно малой.
ДОКАЗАТЕЛЬСТВО. Необходимость.
Пусть
 .
Следовательно,
.
Следовательно,
.
Но это и значит, что последовательность является бесконечно малой.
Достаточность.
Пусть последовательность
является бесконечно малой. Это значит,
что
.
А поскольку условие
 равносильно условию
,
то получаем
равносильно условию
,
то получаем
 ,
что равносильно сходимости последовательности
к числу
.
,
что равносильно сходимости последовательности
к числу
.
ТЕОРЕМА 3.7. Сумма двух бесконечно малых последовательностей является бесконечно малой последовательностью.
ДОКАЗАТЕЛЬСТВО. Пусть
и
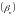 – бесконечно малые последовательности.
Выберем произвольно
– бесконечно малые последовательности.
Выберем произвольно
 и для числа
и для числа
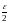 найдем
,
начиная с которого будет выполняться
неравенство
найдем
,
начиная с которого будет выполняться
неравенство
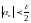 .
Для того же
найдем
,
начиная с которого будет выполняться
неравенство
.
Для того же
найдем
,
начиная с которого будет выполняться
неравенство
 .
Следовательно, выбрав
,
при всех
будем иметь
.
Следовательно, выбрав
,
при всех
будем иметь

 .
Это и значит, что последовательность
.
Это и значит, что последовательность
 является бесконечно малой.
является бесконечно малой.
Замечание. Эту теорему можно обобщить на любое конечное число слагаемых. Например, для доказательства, что сумма трех бесконечно малых последовательностей является бесконечно малой последовательностью, достаточно дважды применить теорему 3.7.
ТЕОРЕМА 3.8. Если
является бесконечно малой последовательностью,
а
– ограниченная последовательность, то
 есть бесконечно малая последовательность.
есть бесконечно малая последовательность.
ДОКАЗАТЕЛЬСТВО. Так как – ограниченная последовательность, то
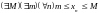 .
.
Пусть
 .
Тогда
.
Тогда
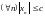 .
Выберем произвольно
и для числа
.
Выберем произвольно
и для числа
 найдем номер
такой, что
найдем номер
такой, что
 .
Тогда при всех
получим
.
Тогда при всех
получим
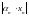 =
= 
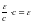 .
Это и значит, что последовательность
является бесконечно малой последовательностью.
.
Это и значит, что последовательность
является бесконечно малой последовательностью.
Последовательность
 ,
где
,
где
 некоторое число, называют постоянной.
Все ее члены равны
некоторое число, называют постоянной.
Все ее члены равны
 .
Очевидно, что такая последовательность
является ограниченной и сходящейся. Ее
пределом является число
:
.
Очевидно, что такая последовательность
является ограниченной и сходящейся. Ее
пределом является число
:
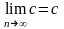 .
.
Следствие
1 Если
– бесконечно малая последовательность,
а
– некоторое действительное число, то
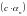 является бесконечно малой последовательностью.
является бесконечно малой последовательностью.
Следствие 2 Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Следствие
3 Если
 –
–
 бесконечно малых последовательностей,
а
бесконечно малых последовательностей,
а
 – действительные числа, то последовательность
(
– действительные числа, то последовательность
( )
является бесконечно малой.
)
является бесконечно малой.
ДОКАЗАТЕЛЬСТВА этих следствий непосредственно вытекают из теорем 3.7 и 3.8.
Определение
3.13. Последовательность
называют бесконечно большой, если
 , т.е. если
, т.е. если

ТЕОРЕМА 3.9. Чтобы
последовательность
была бесконечно большой, необходимо и
достаточно чтобы последовательность
,
где
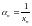 , была бесконечно малой.
, была бесконечно малой.
ДОКАЗАТЕЛЬСТВО. Необходимость.
Пусть
– бесконечно большая последовательность.
Значит
.
Записав неравенство
 в виде
в виде
 и, обозначив
и, обозначив
 через
,
получаем, что
при всех
.
Следовательно,
– бесконечно малая последовательность.
через
,
получаем, что
при всех
.
Следовательно,
– бесконечно малая последовательность.
Достаточность.
Пусть последовательность
,
где
, является бесконечно малой. Следовательно,
.
Обозначив
 через Е, получим определение того, что
последовательность
,
где
через Е, получим определение того, что
последовательность
,
где
 является бесконечно большой.
является бесконечно большой.
