§3. Числовые последовательности.

Рассмотрим числовую функцию , областью определения которой является множество натуральных чисел , т.е. соответствие

Такие функции называют функциями натурального аргумента или числовыми последовательностями. В общем виде числовую последовательность (или просто последовательность) обозначают символом

(*)

или . При этом 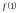называют первым членом последовательности; – вторым, ..., – -ым членом последовательности. Часто для простоты вместо пишут также .

Для последовательностей важны два способа задания:

1. аналитический, т.е. с помощью формулы -го члена вида ;

2. рекуррентный: задают один или несколько первых членов последовательности и формулу, позволяющую определить любой член последовательности по известным предыдущим членам.

Числовые последовательности как функции могут быть ограниченными сверху (снизу), неограниченными, монотонными и немонотонными. Но не имеет смысла ставить вопрос о четности или нечетности последовательности, так как множество не является симметричным. Требует изменения и определение периодичности.

Определение 3.9. Числовую последовательность называют периодической, если . В противном случае последовательность называют непериодической.

Например, последовательность является периодической. Ее члены 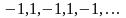повторяются через один, т.е основным периодом является .

Наиболее важными из всех последовательностей являются арифметическая и геометрическая прогрессии.

Арифметической прогрессией называют числовую последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же постоянным числом . Это число называют разностью прогрессии. Если первый член арифметической прогрессии обозначить через , то остальные члены прогрессии по порядку будут иметь вид:

.

Этот факт легко доказать методом математической индукции.

Таким образом, аналитическое задание арифметической прогрессии выглядит так: . Арифметическую прогрессию можно задать и рекуррентно: . Покажем, что каждый член арифметической прогрессии , начиная со второго, равен среднему арифметическому двух соседних с ним членов. Рассмотрим три произвольных члена арифметической прогрессии, идущие подряд. Пусть это будут члены , где произвольное натуральное число. Требуется установить справедливость равенства . Действительно, учитывая, что

,

находим

.

Доказанное свойство является характеристическим для арифметической прогрессии. Его можно обобщить, доказав, что каждый член арифметической прогрессии равен среднему арифметическому двух равноудаленных от него членов прогрессии. Справедливость равенства , где и произвольные натуральные числа, удовлетворяющие условию 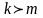, докажите самостоятельно.

Обозначим через сумму первых членов арифметической прогрессии . Выведем формулу для , зная первый член и разность .

Сложим следующие два равенства

Получим .

Заметив, что = , мы получаем, что . Отсюда .

Геометрической прогрессией называют числовую последовательность, в которой первый член отличен от нуля, а каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же постоянное число 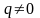. Это число называют знаменателем прогрессии. Если первый член геометрической прогрессии обозначить через : , то остальные члены прогрессии по порядку будут иметь вид: . Это доказывается методом математической индукции.

Таким образом, аналитическое задание геометрической прогрессии выглядит так: . Геометрическую прогрессию можно задать и рекуррентно: . Покажем, что квадрат каждого члена геометрической прогрессии , начиная со второго, равен произведению двух соседних с ним членов. Рассмотрим три произвольных члена геометрической прогрессии, идущие подряд. Пусть это будут члены , где произвольное натуральное число. Требуется установить справедливость равенства . Действительно, . Если все члены геометрической прогрессии положительны, то это свойство можно записать также формулой 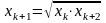. Это означает, что каждый член геометрической прогрессии (с положительными членами), начиная со второго, равен среднему геометрическому двух соседних с ним членов. Это свойство является характеристическим для геометрической прогрессии. Его можно обобщить, показав, что квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух равноотстоящих от него членов прогрессии.

Рассмотрим примеры простейшего исследования числовых последовательностей.

1. .

Последовательность задана аналитически. Выпишем несколько ее первых членов:

1,2,3,4,..., ,...

Это арифметическая прогрессия с разностью 1. Последовательность ограничена снизу, неограничена сверху, монотонно возрастает. Эту же последовательность можно задать рекуррентно:

2. .

Последовательность задана аналитически. Выпишем несколько ее первых членов:

Эта последовательность является ограниченной. Все ее члены положительны и, кроме того, <1 при всех . Покажем, что эта последовательность монотонно возрастает.

> 0.

Значит при любом .

3. .

Последовательность задана рекуррентно. Выпишем несколько ее первых членов:

Это геометрическая прогрессия со знаменателем .

Последовательность монотонно убывает, так как > 0 при любом и , поскольку . Последовательность ограничена (снизу нулем, сверху – числом 2).

4. .

Последовательность задана аналитически. Выпишем несколько ее членов:

Последовательность ограничена (снизу числом -1, сверху – числом ), не является монотонной, так как знаки ее членов чередуются.