2.1. Емпірична функція статистичного розподілу.
Для даної випадкової величини, заданої рядом розподілу
xi |
2 |
5 |
7 |
11 |
15 |
ni |
4 |
6 |
5 |
10 |
20 |
об’єм вибірки дорівнює
N |
45 |
функція розподілу має вигляд
x ≤2 |
0 |
2<x ≤5 |
0,088889 |
5<x ≤7 |
0,222222 |
7<x ≤11 |
0,333333 |
11<x ≤15 |
0,555556 |
x >15 |
1 |
2.2.1. Гістограма частот та відносних частот
Ii |
2-5 |
5-8 |
8-11 |
11-14 |
14-17 |
xi |
3,5 |
6,5 |
9,5 |
12,5 |
15,5 |
ni |
6 |
14 |
20 |
25 |
5 |
ni/h |
2 |
4,666667 |
6,666667 |
8,333333 |
1,666667 |
Wi |
0,085714 |
0,2 |
0,285714 |
0,357143 |
0,071429 |
На осі абсцис відкладемо заданий крок довжиною h=5-2=3. Над цими інтервалами проведемо відрізки, паралельні осі абсцис, на відстані /h, для чого знайдемо:
;
;
;
;
.
Рис. 2.1
Для побудови діаграми відносних частот знайдемо їх густини:
;
;
;
;
Відкладемо
на осі абсцис інтервали. Проведемо над
ними відрізки, паралельні осі абсцис,
на відстані
/h.
Рис. 2.2
2.2.2. Числові характеристики вибірки
;
;
.
2.2.3. Статистичні оцінки генеральної середньої, дисперсії та середнього квадратичного відхилення
;
.
2.3.Висновок: в даній роботі ми працювали з деякими елементами статистичного розподілу, будували гістограму частот та гістограму відносних частот заданої нам вибірки, подали числові характеристики вибірки, підрахували статистичні оцінки генеральної середньої дисперсії та середнього квадратичного відхилення.
Завдання ІІІ. Лінійна кореляція
Теоретичні відомості
Статистична залежність називається кореляційною, якщо у разі зміни однієї величини, змінюється середнє значення іншої.
1. Лінійна кореляція
Якщо обидві лінії регресії Y на X і X на Y – прямі, то кореляцію називають лінійною. Вибіркове рівняння прямої лінії регресії Y на X має вигляд
де
– умовна середня;
і
–
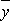вибіркові середні ознак X і Y;
і
– вибіркові середні квадратичні
відхилення X і Y;
– вибірковий коефіцієнт кореляції, причому
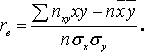
Вибіркове рівняння прямої лінії регресії X на Y має вигляд
Якщо дані спостережень над ознаками X і Y задані у виді кореляційної таблиці з рівновіддаленими варіантами, то доцільно перейти до умовних варіант:
де
– «хибний нуль» варіант X (новий початок
відліку); як хибний нуль вигідно прийняти
варіанту, що розташована приблизно в
середині варіаційного ряду (умовимося
приймати як хибний нуль варіанту, що
має найбільшу частоту);
– крок, тобто різниця між двома сусідніми варіантами X;
– «хибний нуль» варіант Y (новий початок відліку);
– крок, тобто різниця між двома сусідніми варіантами Y.
У цьому випадку вибірковий коефіцієнт кореляції
Величини
,
,
,
можуть бути знайдені або методом
добутків (при великому числі даних), або
безпосередньо за формулами:
Знаючи ці величини, можна обчислити величини, що входять в рівняння регресії за формулами:
Для
оцінки сили лінійного кореляційного
зв'язку служить вибірковий коефіцієнт
кореляції
.
Для обґрунтованого судження про наявність зв'язку між кількісними ознаками варто перевірити, чи значимий вибірковий коефіцієнт кореляції.
Кореляційну залежність у від х можна визначити як функціональну залежність умовної середньої у від х. Виконавши певні алгебраїчні перетворення отримаємо:
(3.1)
–
рівняння
регресії у
на х;
(3.2)
- рівняння регресії х
на у.
Функцію f(x) (або f(y)) називають регресією у на х (або х на у). Графік цієї функції називається лінією регресії.
Тіснота
зв’язку між х та у оцінюється за допомогою
коефіцієнта кореляції
.
Для незалежних величин
=0.
Такі величини називаються некорельованими,
а корельованими є ті величини, у яких
коефіцієнт кореляції відповідно
відмінний від нуля. Якщо |
|> 0,75, це свідчить про наявність зв’язку
між величинами. Якщо |
| > 0,997, то зв'язок між величинами дуже
тісний. Кореляційний коефіцієнт не може
перевищувати 1.
3.1. Рівняння прямих ліній регресії X на Y, Y на X;
|
1-9 |
9-17 |
17-25 |
25-33 |
33-41 |
41-49 |
ny |
y |
V |
nyV |
nyV2 |
q |
qV |
13-23 |
5 |
7 |
|
|
|
|
12 |
18 |
-2 |
-24 |
48 |
-23 |
46 |
23-33 |
|
6 |
8 |
|
|
|
14 |
28 |
-1 |
-14 |
14 |
-13 |
13 |
33-43 |
|
|
4 |
40 |
5 |
|
49 |
38 |
0 |
0 |
0 |
25,5 |
0 |
43-53 |
|
|
6 |
12 |
2 |
|
20 |
48 |
1 |
20 |
20 |
6 |
6 |
53-63 |
|
|
|
1 |
3 |
2 |
6 |
58 |
2 |
12 |
24 |
10 |
20 |
nx |
5 |
13 |
18 |
53 |
10 |
2 |
101 |
|
|
-6 |
106 |
|
85 |
x |
5 |
13 |
21 |
29 |
37 |
45 |
|
|
|
|
|
|
|
U |
-2,5 |
-1,5 |
-0,5 |
0,5 |
1,5 |
2,5 |
|
|
|
|
|
|
|
nxU |
-12,5 |
-19,5 |
-9 |
26,5 |
15 |
5 |
5,5 |
|
|
|
|
|
|
nxU2 |
31,25 |
29,25 |
4,5 |
13,25 |
22,5 |
12,5 |
113,25 |
|
|
|
|
|
|
t |
-10 |
-20 |
-2 |
14 |
8 |
4 |
|
|
|
|
|
|
|
tU |
25 |
30 |
1 |
7 |
12 |
10 |
85 |
|
|
|
|
|
|
Табл. 3.1.
Результати
обчислень будемо записувати до
кореляційної таблиці (табл. 3.1). Перейдемо
від початкових варіант
та
до умовних варіант:
і
,
де
.
Як
візьмемо варіанту х=29,
що має найбільшу частоту
,
як
- варіанту у=38,
що має найбільшу частоту
.
Елементи
рядка
дорівнюють
добуткам відповідних елементів рядків
і u;
елементи стовпця
дорівнюють
добуткам відповідних елементів стовпця
і v;
аналогічно заповнюємо рядок
і стовпець
.
Кожен
елемент стовпця q
дорівнює сумі добутків частот
,
які знаходяться у відповідному рядку
вихідної кореляційної таблиці, на
відповідні елементи рядка u:
У рядку t кожен елемент дорівнює сумі добутків частот , які знаходяться у відповідному стовпці кореляційної таблиці, на відповідні елементи стовпця v:
і
т.д.
У
стовпці qv
кожен елемент дорівнює добутку відповідних
елементів і стовбців q
і v,
в останньому ряду кожен елемент дорівнює
добутку відповідних елементів t
і u.
Рівність сум
використовується для контролю правильності
обчислень.
Далі знаходимо:
Тепер знайдемо:
;
;
;
.
Підставивши знайдені величини в (3.1), отримаємо шукане рівняння:
-
рівняння регресії у
на х;
Порівняємо у з рівняння регресії і у, підрахований за таблицею:
x |
yx |
yx*табл |
5 |
18,1087 |
18 |
13 |
25,66304 |
22,61538 |
21 |
33,21739 |
36,88889 |
29 |
40,77174 |
40,64151 |
37 |
48,32609 |
46 |
45 |
55,88043 |
58 |
Підставивши знайдені величини в (3.1), отримаємо шукане рівняння:
рівняння
регресії х
на у.
Порівняємо х з рівняння регресії і х*, підрахований за таблицею:
YI |
ẍy |
ẍy* |
18 |
9,666667 |
12,89653 |
28 |
17,57143 |
19,35801 |
38 |
29,16327 |
25,81949 |
48 |
27,4 |
32,28097 |
58 |
38,33333 |
38,74246 |
3.2. Знайдемо коефіцієнт кореляції:
Зв'язок між величинами наявний, але він не дуже тісний.
3.3.Висновок: в даній роботі ми знаходили рівняння прямих ліній регресії X на Y, Y на X, розрахували вибірковий коефіцієнт кореляції та оцінили силу зв’язку Y і X
.
Додаток 1
|
поліном першого порядку |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
№ |
x |
y |
x2 |
xy |
y^ |
(y-y^)2 |
|||
1 |
10 |
141,1 |
=B26^2 |
=B26*C26 |
=$E$40+$F$40*B26 |
=(C26-F26)^2 |
|||
2 |
20 |
130 |
=B27^2 |
=B27*C27 |
=$E$40+$F$40*B27 |
=(C27-F27)^2 |
|||
3 |
30 |
111,7 |
=B28^2 |
=B28*C28 |
=$E$40+$F$40*B28 |
=(C28-F28)^2 |
|||
4 |
40 |
86,1 |
=B29^2 |
=B29*C29 |
=$E$40+$F$40*B29 |
=(C29-F29)^2 |
|||
5 |
50 |
58,4 |
=B30^2 |
=B30*C30 |
=$E$40+$F$40*B30 |
=(C30-F30)^2 |
|||
6 |
60 |
29,1 |
=B31^2 |
=B31*C31 |
=$E$40+$F$40*B31 |
=(C31-F31)^2 |
|||
7 |
70 |
9,56 |
=B32^2 |
=B32*C32 |
=$E$40+$F$40*B32 |
=(C32-F32)^2 |
|||
сума |
=СУММ(B26:B34) |
=СУММ(C26:C34) |
=СУММ(D26:D34) |
=СУММ(E26:E34) |
|
=СУММ(G26:G34) |
|||
=A32 |
=B33 |
=C33 |
|
a0 |
a1 |
=B33 |
=D33 |
=E33 |
|
=C50 |
=C49 |
середня кв. похибка |
=КОРЕНЬ(G33/A32) |
схема єдиного ділення
x1
x2
b
сума
=A39
=B39
=C39
=A44+B44+C44
=A40
=B40
=C40
=A45+B45+C45
=A44/A44
=B44/A44
=C44/A44
=D44/A44
=B45-A45*B46
=C45-A45*C46
=B47+C47
=B47/B47
=C47/B47
=B48+C48
1
=C48
=D48
1
=C46-B46*C49
=D46-B46*D49
поліном другого порядку
№
x
y
x2
x3
x4
xy
x2y
1
=B26
=C26
=B56^2
=B56^3
=B56^4
=B56*C56
=D56*C56
2
=B27
=C27
=B57^2
=B57^3
=B57^4
=B57*C57
=D57*C57
3
=B28
=C28
=B58^2
=B58^3
=B58^4
=B58*C58
=D58*C58
4
=B29
=C29
=B59^2
=B59^3
=B59^4
=B59*C59
=D59*C59
5
=B30
=C30
=B60^2
=B60^3
=B60^4
=B60*C60
=D60*C60
6
=B31
=C31
=B61^2
=B61^3
=B61^4
=B61*C61
=D61*C61
7
=B32
=C32
=B62^2
=B62^3
=B62^4
=B62*C62
=D62*C62
сума
=СУММ(B56:B62)
=СУММ(C56:C62)
=СУММ(D56:D62)
=СУММ(E56:E62)
=СУММ(F56:F62)
=СУММ(G56:G62)
=СУММ(H56:H62)
y^
(y-y^)2
=$F$68+$G$68*B56+$H$68*(B56^2)
=(C56-I56)^2
=$F$68+$G$68*B57+$H$68*(B57^2)
=(C57-I57)^2
=$F$68+$G$68*B58+$H$68*(B58^2)
=(C58-I58)^2
=$F$68+$G$68*B59+$H$68*(B59^2)
=(C59-I59)^2
=$F$68+$G$68*B60+$H$68*(B60^2)
=(C60-I60)^2
=$F$68+$G$68*B61+$H$68*(B61^2)
=(C61-I61)^2
=$F$68+$G$68*B62+$H$68*(B62^2)
=(C62-I62)^2
=СУММ(J56:J62)
|
коефіцієнти |
|
|
|
|
|
|
=A62 |
=B63 |
=D63 |
=C63 |
|
|
|
|
=B63 |
=D63 |
=E63 |
=G63 |
|
a0 |
a1 |
a2 |
=D63 |
=E63 |
=F63 |
=H63 |
|
=F87 |
=F86 |
=F85 |
середня кв. похибка |
|
=КОРЕНЬ(J63/A62) |
|
схема єдиного ділення
хід |
етапи |
коефіцієнти |
|
b |
суми |
||||
|
|
x1 |
x2 |
x3 |
|
|
|
||
прямий |
1 |
=A68 |
=B68 |
=C68 |
=D68 |
=C76+D76+E76+F76 |
=B76+C76+D76+E76+F76 |
||
|
|
=A69 |
=B69 |
=C69 |
=D69 |
=C77+D77+E77+F77 |
=C77+D77+E77+F77 |
||
|
|
=A70 |
=B70 |
=C70 |
=D70 |
=C78+D78+E78+F78 |
=C78+D78+E78+F78 |
||
|
|
=C76/C76 |
=D76/C76 |
=E76/C76 |
=F76/C76 |
=G76/C76 |
=C79+D79+E79+F79 |
||
|
2 |
|
=D77-C77*D79 |
=E77-C77*E79 |
=F77-C77*F79 |
=D80+E80+F80 |
=D80+E80+F80 |
||
|
|
|
=D78-C78*D79 |
=E78-C78*E79 |
=F78-C78*F79 |
=D81+E81+F81 |
=D81+E81+F81 |
||
|
|
|
=D80/D80 |
=E80/D80 |
=F80/D80 |
=G80/D80 |
=D82+E82+F82 |
||
|
3 |
|
|
=E81-D81*E82 |
=F81-D81*F82 |
=E83+F83 |
=E83+F83 |
||
|
|
|
|
=E83/E83 |
=F83/E83 |
=G83/E83 |
=E84+F84 |
||
зворотній |
4 |
|
|
1 |
=F84 |
=G84 |
=E85+F85 |
||
|
|
|
1 |
|
=F82-E82*F85 |
=G82-E82*G85 |
=D86+F86 |
||
|
|
1 |
|
|
=F79-E79*F85-D79*F86 |
=G79-E79*G85-D79*G86 |
=C87+F87 |
||
Додаток 2
2.1) |
|
|
|
|
|
xi |
2 |
5 |
7 |
11 |
15 |
ni |
4 |
6 |
5 |
10 |
20 |
N |
=B3+C3+D3+E3+F3 |
|
|
|
|
x ≤2 |
0 |
|
|
|
|
2<x ≤5 |
=B3/B4 |
|
|
|
|
5<x ≤7 |
=(B3+C3)/B4 |
|
|
|
|
7<x ≤11 |
=(B3+C3+D3)/B4 |
|
|
|
|
11<x ≤15 |
=(B3+C3+D3+E3)/B4 |
|
|
|
|
x >15 |
=(B3+C3+D3+E3+F3)/B4 |
|
|
|
|
2.2) |
|
|
|
|
|
|
|
|
|
|
|
Ii |
2-5 |
5-8 |
8-11 |
11-14 |
14-17 |
ni |
6 |
14 |
20 |
25 |
5 |
|
|
|
|
|
|
ni/h |
=B16/H15 |
=C16/H15 |
=D16/H15 |
=E16/H15 |
=F16/H15 |
Wi |
=B16/H16 |
=C16/H16 |
=D16/H16 |
=E16/H16 |
=F16/H16 |
Wi/h |
=B19/H15 |
=C19/H15 |
=D19/H15 |
=E19/H15 |
=F19/H15 |
|
|
|
|
|
|
Ii |
2-5 |
5-8 |
8-11 |
11-14 |
14-17 |
ni |
6 |
14 |
20 |
25 |
5 |
xi |
=(2+5)/2 |
=(5+8)/2 |
=(8+11)/2 |
=(11+14)/2 |
=(14+17)/2 |
N |
=B23+C23+D23+E23+F23 |
xв |
=(B23*B24+C23*C24+D23*D24+E23*E24+F23*F24)/I24 |
DB |
=((B23*(B24-I25)^2)+(C23*(C24-I25)^2)+(D23*(D24-I25)^2)+(E23*(E24-I25)^2)+(F23*(F24-I25)^2))/I24 |
σB |
=КОРЕНЬ(I26) |
xr |
=I25 |
D |
=(I26/(I24-1))*I24 |
σr |
=КОРЕНЬ(I29) |
Додаток 3
Ū |
=I14/I11 |
|
|
|
|
|
|
Ṽ |
=L11/I11 |
|
|
|
|
|
|
Ϭu |
=КОРЕНЬ((I15/I11)-(C19^2)) |
|
|
|
|
|
|
Ϭv |
=КОРЕНЬ((M11/I11)-(C20^2)) |
|
|
|
|
|
|
rв |
=(I17-(I11*C19*C20))/(I11*C21*C22) |
|
|
|
|
|
|
ẍ |
=(C19*8)+R10 |
|
|
|
|
|
|
ȳ |
=(C20*10)+J8 |
|
|
|
|
|
|
Ϭx |
=C21*8 |
|
|
|
|
|
|
Ϭy |
=C22*10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
=(C23*C27)/C26 |
=((C23*C27)/C26)*(-C24)+C25 |
|
ȳx=0,944293x+13038723 |
|
||
|
|
|
|
|
|
|
|
XI |
ȳx |
ȳx* |
ȳx*-ȳx |
|
|
|
|
=C5 |
=(C6*B6)/C11 |
=$C$26*B32+$D$26 |
=D32-C32 |
|
|
|
|
=D5 |
=(D6*B6+D7*B7)/D11 |
=$C$26*B33+$D$26 |
=D33-C33 |
|
|
|
|
=E5 |
=(E7*B7+E8*B8+E9*B9)/E11 |
=$C$26*B34+$D$26 |
=D34-C34 |
|
|
|
|
=F5 |
=(F8*B8+F9*B9+F10*B10)/F11 |
=$C$26*B35+$D$26 |
=D35-C35 |
|
|
|
|
=G5 |
=(G8*B8+G9*B9+G10*B10)/G11 |
=C29*B36+D29 |
=D36-C36 |
|
|
|
|
=H5 |
=(H10*B10)/H11 |
=C29*B37+D29 |
=D37-C37 |
|
|
|
|