Національний технічний університет України

«Київський політехнічний інститут»

Домашня контрольна робота

З дисципліни Обчислювальна математика та програмування

Тема: Математична обробка експериментальних даних

Роботу виконав

Студент ІХФ гр. ЛЦ-21

Шишкіна С.О.

Перевірив:

К. т. н. доц. Сангінова О. В.

Київ 2012

Зміст

Завдання до ДКР………………………………………………………………………………...3

Вступ……………………………………………………………………………………………..4

1 Для заданої табличнох функції (Додаток 1) виконати наступні дії :

Отримати апроксимуючої функції

1.1. Визначити загальний вид апроксимуючої залежності, побудувавши точковий графік заданої функції;..............................................................................................................................7

1.2. Апроксимувати задану табличну функцію поліномом першого порядку……………....8

1.3. Апроксимувати задану табличну функцію поліномом другого порядку………………..9

1.4. Оцінити точність апроксимації …………………………………………………...……...10

1.4.1. обчисливши середню квадратичну похибку;……………………………………….….11

1.4.2. побудувавши графік отриманих апроксимованих функцій і порівнявши їх з точковим графіком заданої функції………………………………………………….………..12

1.5. Зробити висновки…………………………………………………………………...……..12

2. За результатами експериментальних даних (Додоток 2) :

2.1. За даними таблиці 2.1 (де х_і-варіанти, n_i-частоти варіанти х_і, (і=1,2,3,4,5)), знайти емпіричну функцію статистичного розподілу (аналітично і графічно)………………….16

2.2. За даними таблиці 2.2 (де I_i і-ий інтервал; n_i-сума частот варіант, які потрапили в і-тий інтервал):

2.2.1. побудувати гістограми частот та відносних частот;……………………….….……17

2.2.2. знайти числові характеристики статистичного розподілу:вибіркову середню х_В , вибіркову дисперсію D_B , вибіркове середнє квадратичне відхилення σ_В;………...……18

2.2.3. знайти статистичні оцінки генеральної середньої, генеральної дисперсії і генерального середнього квадратичного відхилення…………………..…………………18

2.3. Зробити висновки…………………………………………………………………………18

3. На а основі експериментальних даних, отриманих для вивчення залежності між випадковими величинами X і y, і представленими у вигляді кореляційної таблиці (Додаток 3):

3.1. Знайти рівняння прямих ліній регресії X на Y, Y на X…………………..…………..24

3.2. Розрахувати вибірковий коефіцієнт кореляції та оцінити силу зв’язку Y і X……...24

3.3. Зробити висновки…………………………….…………………………………………24

Список використаної літератури…………………………………………………….…….25

Завдання

Завдання 1. Отримати апроксимуючу функцію:

P	C
10	141,1
20	130
30	111,7
40	86,1
50	58,4
60	29,1
70	9,65

1.1. Визначити загальний вид апроксимуючої залежності, побудувавши точковий графік заданої функції;

1.2. Апроксимувати задану табличну функцію поліномом першого порядку.

1.3. Апроксимувати задану табличну функцію поліномом другого порядку.

1.4. Оцінити точність апроксимації

1.4.1. обчисливши середню квадратичну похибку;

1.4.2. побудувавши графік отриманих апроксимованих функцій і порівнявши їх з точковим графіком заданої функції.

Завданняи 2. За результатами експериментальних даних:

2.1. За даними таблиці 2.1 (де х_і-варіанти, n_i-частоти варіанти х_і, (і=1,2,3,4,5)), знайти емпіричну функцію статистичного розподілу (аналітично і графічно).

xi	2	5	7	11	15
ni	4	6	5	10	20

2.2. За даними таблиці 2.2 (де I_i і-ий інтервал; n_i-сума частот варіант, які потрапили в і-тий інтервал):

Ii	2-5	5-8	8-11	11-14	14-17
ni	6	14	20	25	5

2.2.1. побудувати гістограми частот та відносних частот;

2.2.2. знайти числові характеристики статистичного розподілу:вибіркову середню х_В , вибіркову дисперсію D_B , вибіркове середнє квадратичне відхилення σ_В ;

2.2.3. знайти статистичні оцінки генеральної середньої, генеральної дисперсії і генерального середнього квадратичного відхилення.

Завдання 3. На а основі експериментальних даних, отриманих для вивчення залежності між випадковими величинами X і Y, і представленими у вигляді кореляційної таблиці:

3.1. Знайти рівняння прямих ліній регресії X на Y, Y на X

3.2. Розрахувати вибірковий коефіцієнт кореляції та оцінити силу зв’язку Y і X

	5	13	21	29	37	45
18	5	7
28		6	8
38			4	40	5
48			6	12	2
58				1	3	2

Вступ

В даній роботі виконана математична обробка експериментальних даних за допомогою апроксимації функції, статистичного розподілу, а також використовуючи метод лінійної кореляції.

Для визначення виду апроксимуючої функції у завданні І було використано: графічний метод, апроксимація поліномом другого порядку. Для оцінки точності апроксимації розраховано середню квадратичну похибку. Різницю між апроксимуючою та заданою функції можна прослідкувати на побудованих графіках цих функцій.

У завданні ІІ дані статистичного розподілу зображені у вигляді гістограми частот та відносних частот. З допомогою даних було розраховано такі числові характеристики, як вибіркова середня, дисперсія, середнє квадратичне відхилення, знайдено статистичні оцінки генеральної вибіркової середньої, дисперсії.

У завданні ІІІ за даними кореляційної таблиці знайдено рівняння прямих ліній регресії У на Х, та Х на У, а також оцінено силу кореляційного зв’язку.

Теоретичні відомості

Нехай дослідним шляхом отримані значення деякої величини у для заданих значень величини х та подані у вигляді таблиці:

х	х1	х2	…	xn
у	y1	y2	…	yn

Табл. 1.1

Характер функціональної залежності між величинами у та х невідомий; потрібно знайти аналітичний вираз залежності між х та у, який називається емпіричною формулою.

Геометрично задача побудови емпіричної формули полягає в проведенні такої кривої (чи прямої), що була б досить близько розташована до дослідних точок (хі;уі) (і=1, 2, …, n).

Нехай функція y=f(x) задана своїми значеннями , , …, 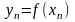. Потрібно знайти апроксимуючий багаточлен першого степеня:

(1.1)

такий, щоб квадратичне відхилення

(1.2)

було мінімальним.

Середнє квадратичне відхилення обчислюється з формулою:

. (1.3)

Нормальна система для визначення , матиме такий вигляд:

Виконавши найпростіші перетворення, отримаємо

(1.4)

Систему (1.4) зручно розв’язати з використанням формул Крамера. Знайдені значення коефіцієнтів і підставляємо у вираз (1.1) і, отже, одержуємо конкретний вигляд апроксимуючого багаточлена .

На практиці нелінійну залежність у від х часто апроксимують поліномом другого порядку:

, (1.5)

де - коефіцієнти, що підлягають визначенню.

Нормальна система для визначення матиме вигляд:

(1.6)