МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

Кафедра радиоэлектроники и защиты информации (РЗИ)

Пояснительная записка к курсовой работе по дисциплине

«Теория вероятностей и математическая статистика»

Студентка группы 181

_____ Д.А. Скворцова

Руководитель:

Доцент кафедры РЗИ

________ Г.Н. Глазов

2012

РЕФЕРАТ

Курсовая работа 24 с., 3 рис., 5 источников.

РЕГРЕСИОННЫЙ АНАЛИЗ, ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ, ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ, КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА, МЕТОД НАИМЕНЬШИХ КВАДРАТОВ, НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ.

Объектом исследования являются генеральная совокупность и функция сигнал + шум.

Целью курсовой работы является закрепление теоретических знаний и получение практических навыков расчета доверительных интервалов и критериев согласия для различных числовых характеристик, а также восстановление сигнала из смеси – сигнал+шум, используя метод наименьших квадратов.

В результате проведенной работы были закреплены теоретические знания и приобретены практические навыки работы со статистиками и использования классического регрессионного анализа.

Разработанный программный продукт может быть использован для проведения регрессионного анализа.

Пояснительная записка выполнена в текстовом редакторе Microsoft Word 2010.

В качестве рабочей среды был использован пакет Mathcad 15.

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ

Кафедра радиоэлектроники и защиты информации (РЗИ)

УТВЕРЖДАЮ

Зав. кафедрой РЗИ, профессор

____________А.С. Задорин

«___»_____________201_г.

ЗАДАНИЕ

на курсовую работу по дисциплине

''Теория вероятностей и математическая статистика"

Тема работы: Курсовая работа по математической статистике

Исполнитель –__Скворцова Д._группа_181______

Цель работы: Целью данной работы является изучение методов анализа экспериментальных данных и метода классического регрессионного анализа.

Здесь будет текст задания, который я написал в Замечаниях. Если места не хватит, то убери пустые места в тексте ниже.

Содержание работы:

Введение

1. Постановка задачи

2. Часть 1. Критерий согласия Пирсона.

   1. Теоретические сведения.

   2. Практическая работа.

   3. Выводы.

3. Часть 2. Классический регрессионный анализ (мнк)

   1. Теоретические сведения.

   2. Практическая работа.

   3. Выводы.

4. Заключение.

5. Список использованных источников.

Руководитель курсовой работы Задание получил

Доцент каф. РЗИ Студентка гр.

Ген. Н. Глазов _______________ ________________________

Дата выдачи задания "__"___ 2012 г. Срок сдачи работы "__"___2012 г.

2012

СОДЕРЖАНИЕ

ВВЕДЕНИЕ ………………………………………………………………………… ...5

1. Постановка задачи ……………………………………………………………...... 6

2. Часть I. Критерий согласия Пирсона ……………………………………………8

   1. Теоритические сведенья …………………………………………………... …8

   2. Расчеты………………………………………………………………………...12

   3. Выводы ………………………………………………………………………..16

3. Часть II. Регрессионный анализ ………………………………………………....17

   1. Теоритические сведенья ……………………………………………………..17

   2. Расчеты ………………………………………………………………………..19

   3. Выводы ……………………………………………………………………… ..22

4. Заключение ………………………………………………………………………. 23

Список использованных источников ……………………………………………24

ВВЕДЕНИЕ

Целью данной курсовой работы является получение практических знаний в сфере

точечного и интервального оценивания, проверки гипотез, а также освоение одного из методов расчета в регрессионном анализе.

Курсовая работа состоит из двух частей. Первая часть посвящена проверке с помощью критерия Пирсона гипотезы о том, что выборка извлечена из нормальной генеральной совокупности, вторая часть - классическому регрессионному анализу.

Каждая из частей содержит теоретический обзор, математические расчеты и выводы о проделанной работе.

1. ПОСТАНОВКА ЗАДАЧИ

Работа состоит из двух частей.

В первой части приводится краткий обзор теоретических сведений, включающий:

1. Оценки мат. ожидания и дисперсии,

2. Нахождение доверительных интервалов

3. Проверку с помощью критерия Пирсона гипотезу о том, что выборка извлечена из нормальной генеральной совокупности.

Во второй части приводится краткий обзор теоретических сведений, посвящённый:

1. Регрессионному анализу

2. Методу наименьших квадратов.

Часть I

Дана выборка из N =100 значений.

Требуется:

а) найти статистический ряд;

б) построить гистограмму и полигон частот;

в) найти оценки для математического ожидания и дисперсии;

г) считая распределение генеральной совокупности нормальным, найти границы доверительного интервала для математического ожидания и дисперсии при надёжности

γ = 0,95;

д) проверить с помощью критерия χ² гипотезу о том, что выборка извлечена из нормальной генеральной совокупности с математическим ожиданием и средним квадратическим отклонением равными соответственно статистическому среднему и статистическому среднему квадратичному отклонению. Уровень значимости принять равным α = 0,05.

Часть II

В Mathcad (вне зависимости от версии) имеются датчики (генераторы) случайных чисел с разнообразными законами распределения. В частности, rnorm(m,μ,σ) возвращает вектор m случайных чисел, имеющих нормальное распределение с математическим ожиданием μ и среднеквадратическим отклонением σ. Будем использовать rnorm(m,0,1) — датчик нормальных случайных чисел с нулевым математическим ожиданием и единичной дисперсий.

Истинный тренд задан функцией:

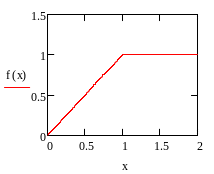
Сигнал + шум имеет вид:

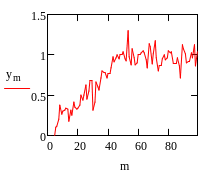
2 ЧАСТЬ I. КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА.

2.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Параметры законов распределения обычно оцениваются по выборке, т.е. строится такая функция выборочных данных, что она мало отличается от истинного значения параметра.

Существуют разные способы оценивания:

1. Точечные оценки – оценка в виде числа – точка на оси

2. Интервальная оценка – находится некий интервал [a,b], в котором находится наш истинный параметр с заданной нами вероятностью.

Чем выше доверительная вероятность того что параметр находится внутри, тем шире интервал, и наоборот чем ниже вероятность, тем уже интервал.

2.1.1 ПОНЯТИЕ СТАТИСТИЧЕСКОГО РЯДА

Результаты сводки и группировки материалов статистического наблюдения оформляются в виде статистических рядов распределения.  Статистические ряды распределения представляют собой упорядоченное распределение единиц изучаемой совокупности на группы по группировочному (варьирующему) признаку, т.е. пары середин подинтервалов и абсолютных частот. Они характеризуют состав (структуру) изучаемого явления, позволяют судить об однородности совокупности, границах ее изменения, закономерностях развития наблюдаемого объекта.

2.1.2 ПОЛИГОН ЧАСТОТ И ГИСТОГРАММА

Полигоном частот называют ломанную, отрезки которой соединяют точки (x₁; n₁), (x₂; n₂), ..., (x_k; n_k), где xi – середина подинтервала и ni – абсолютная частота. Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им частоты n_i. Точки ( x_i; n_i) соединяют отрезками прямых и получают полигон частот .

Гистограммой абсолютных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы шириной h, а высоты равны отношению n_i /h.

2.1.3. ОЦЕНКА НЕИЗВЕСТНЫХ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ.

ТОЧЕЧНОЕ ОЦЕНИВАНИЕ

Оценка математического ожидания

Оценкой математического ожидания является выборочное среднее

Оценка дисперсии

Оценкой дисперсии будет выборочная дисперсия:

2.1.4. ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ.

При статистической обработке результатов наблюде­ний часто необходимо не только найти оценку θ^’ неизвестного параме­тра θ, но и охарактеризовать точность этой оценки. С этой целью вво­дится понятие доверительного интервала.

Доверительным интервалом для параметра θ называется интервал (θ₁, θ ₂), содержащий (накрывающий) истинное значение θ с заданной вероятностью ρ = 1 — α, т.е.

Ρ [θ₁ < θ < θ₂] = 1 - α. (1)

Число 1 — α называется доверительной вероятностью, а значение α — уровнем значимости. Статистики θ₁ = θ₁(x₁, ..., x_n) и θ₂ = θ₂(x₁, ..., x_n), определяемые по выборке

x₁, ..., х_п из генеральной совокупности с неизвестным параметром 0, называются соответственно нижней и верхней границами доверительного интервала.

Условие (1) означает, что в большой серии независимых экспери­ментов, в каждом из которых получена выборка объема п, в среднем (1 — а) 100% из общего числа построенных доверительных интервалов содержат истинное значение параметра 0.

Длина доверительного интервала, характеризующая точность интер­вального оценивания, зависит от объема выборки n и доверительной ве­роятности 1 — α: при увеличении объема выборки длина доверительного интервала уменьшается, а с приближением доверительной вероятности к единице — увеличивается. Выбор доверительной вероятности опреде­ляется конкретными условиями. Обычно используются значения 1 — α, равные 0,90; 0,95; 0,99.

При решении некоторых задач применяются односторонние довери­тельные интервалы, границы которых определяются из условий

Ρ [θ < θ₂] = 1 - α или Ρ [θ₁ < θ] = 1 - α.

Эти интервалы называются соответственно левосторонними и право­сторонними доверительными интервалами.

Чтобы найти доверительный интервал для параметра θ, необходимо знать закон распределения статистики θ^’ = θ^’ (x₁, ..., х_п), значение ко­торой является оценкой параметра θ. При этом для получения довери­тельного интервала наименьшей длины при данном объеме выборки n и заданной доверительной вероятности 1 — α в качестве оценки θ пара­метра θ следует брать эффективную либо асимптотически эффективную оценку.

2.1.5. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА.

Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Пусть по выборке объема n получено эмпирическое распределение:

С помощью критерия Пирсона можно проверить гипотезу о различных законах распределения генеральной совокупности (равномерном, нормальном, показательном и др.) Для этого в предположении о конкретном виде распределения вычисляются теоретические частоты n_i^’ , и в качестве критерия выбирается случайная величина.

имеющая закон распределения χ2 с числом степеней свободы k = s – 1 – r, где s – число частичных интервалов выборки, r – число параметров предполагаемого распределения. Критическая область выбирается правосторонней, и граница ее при заданном уровне значимости α находится по таблице критических точек распределения χ2.

Теоретические частоты n_i^’ вычисляются для заданного закона распределения

как количества элементов выборки, которые должны были попасть в каждый интервал, если бы случайная величина имела выбранный закон распределения, параметры которого совпадают с их точечными оценками по выборке, а именно:

а) для проверки гипотезы о нормальном законе распределения n_i^’= n · Р_i, где

n – объем выборки, , , x_i и x_i+1 левая и правая

границы i-го интервала, - выборочное среднее, s – исправленное среднее квадратическое отклонение. Поскольку нормальное распределение характеризуется двумя параметрами, число степеней свободы k = n – 3.

2.1.6. КВАНТИЛЬ

Квантиль - значение, которое заданная случайная величина не превышает с фиксированной вероятностью.

Квантилью уровня P, называется решение уравнения 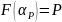, где P и F заданы.

Рис.1 Квантиль уровня P

Квантиль P – значение случайной величины, при котором функция распределения равна P.

В данной работе будут использованы квантили распределения Стьюдента и хи-квадрат Пирсона.

2.2 РАСЧЁТЫ

Данная выборка

объем выборки

сортировка массива

размах выборки

ширина подынтервала

границы подынтервалов обозначим другими буквами

цикл формирования абсолютных частот

_{обнуление}

f - это вектор строка записанный из выборки

проверка правильности нахождения частот

Построим гистограмму, но она не нормированная - высота прямоугольников равна

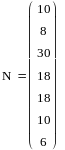
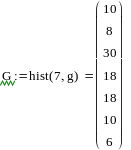
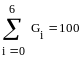
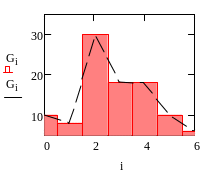
Введем в рассмотрение середины подынтервалов

Вычислим точечные оценки математического ожидания и среднего квадратичного значения

Доверительные интервалы

Для мат. ожидания

квантиль

значение квантили из таблицы

где m истинное значение мат. ожидания

Для дисперсии

квантиль распределения хи квадрат для левой границы

квантиль распределения хи квадрат для правой границы

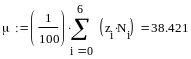
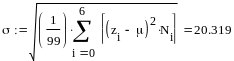
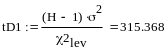
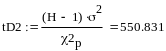
Проверим с помощью критерия Пирсона гипотезу о том, что выборка извлечена из нормальной генеральной совокупности с σ и μ (оценки)

Пользуемся функцией Гаусса вида:

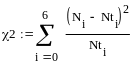
выборочное значение распределения Пирсона

критическое значение распределения

Гипотезу о нормальном распределении выборки отвергаем

2.3. ВЫВОДЫ

В ходе работы над первой частью курсовой работы был написан подробный

теоретический обзор. Также были решены данные задачи. Получен опыт нахождения статистического ряда, построения гистограммы и полигона частот. После проверки гипотезы было выяснено, что теоретическое меньше, чем практическое. Это означает, что нормальный закон распределения для данной совокупности не подходит.

3 ЧАСТЬ II. РЕГРЕССИОННЫЙ АНАЛИЗ

3.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Часто у инженера возникает задача выделения сигнала из смеси «сигнал + шум».

Например, на промежутке от t₁ до t₂ функция f(t) имеет вид, но в силу патологического влияния шумов и помех эта кривая превратилась в смесь y(t)=f(t) + n(t).

Реально мы владеем какой-то информацией и о сигнале и о шуме, но этого недостаточно.

Алгоритм восстановления сигнала из смеси «сигнал + шум»:

1. Задается функция f(t)

2. Генерируется шум с помощью датчика случайных чисел n(t).

3. Построим сумму f(t) + n(t).

4. Принимаем модель f(t) в виде полинома третьей степени – кубической параболы. Находим методом МНК коэффициенты этой кубической параболы. Они будут являться функциями y(t).

3.1.1 МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК)

Метод наименьших квадратов (МНК) – это метод оценки неизвестных случайных величин по результатам измерений, содержащим случайные ошибки. В нашем случае дана смесь – сигнал+шум. Наша задача состоит в извлечении истинного тренда.

При помощи метода наименьших квадратов вычисляются коэффициенты аппроксимирующего многочлена. Эта задача решается следующим образом.

Пусть на некотором отрезке в точках … 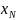нам известны значения … 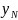некоторой функции f(x).

Требуется определить параметры 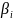многочлена вида

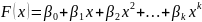, где k<N

такого, что сумма квадратов отклонений значений y от значений функции f(y) в заданных точках x была бы минимальной, то есть .

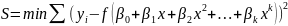Геометрический смысл заключается в том, что график найденного многочлена y = f(x) будет проходить как можно ближе к каждой из заданных точек.

Далее нужно решить следующую систему уравнений:

…………………………………………………………………………….

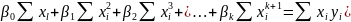
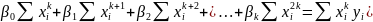
Запишем систему уравнений в матричном виде:

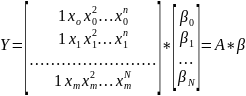
Решением является следующее выражение:

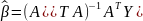
Несмещенная оценка для дисперсии ошибок наблюдений равна:

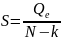
Чем величина S меньше, тем точнее описывается Y.

N – Объем выборки

k-Число параметров тренда –

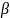
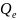считается по формуле:

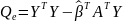
Доверительный интервал для коэффициентов тренда считается так:

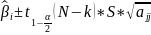
j=0..3

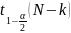– квантиль распределения Стьюдента

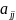- jj-ый диагональный элемент матрицы .

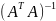3.2 РАСЧЕТЫ

РЕГРЕССИОННЫЙ АНАЛИЗ

текущий индекс

датчик случайных значений

_шаг

вычисление вектора коэффициентов

_модель

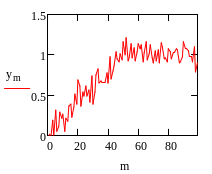
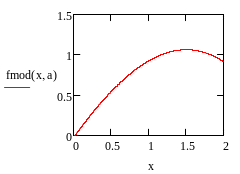
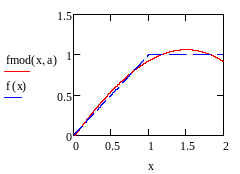
Изобразим на одной плоскости данную функцию и модель полученную с помощью МНК

Доверительные интервалы

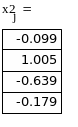
вектор коэффициентов

число, сумма квадратов шумовых слагаемых

несмещенная оценка дисперсии ошибок наблюдений

квантиль, находим в таблице

3.3 ВЫВОДЫ

В ходе работы была решена задача нахождения истинного тренда из смеси

сигнал +шум. За основу работы взят метод наименьших квадратов. Для оптимальных

расчетов был использован полином третьей степени, что свелось к нахождению четырёх коэффициентов модели. Были рассчитаны не только сами коэффициенты, но и

доверительные интервалы для них. На построенном графике представлены два тренда –

истинный и его оценка. Имеются небольшие отклонения, это связано с тем, что было

взято относительно небольшое количество коэффициентов.

4. ЗАКЛЮЧЕНИЕ

В ходе выполнения данной курсовой работы был получен опыт нахождения

точечной оценки и доверительного интервала для таких величин, как математическое

ожидание и дисперсия, закреплены навыки построения гистограммы и полигона частот

для некоторой выборки значений.

Так же был освоен метод наименьших квадратов (МНК), как один из способов

в регрессионном анализе для извлечения истинного тренда из смеси сигнал + шум.

Полученные в ходе работы навыки можно использовать не только в учебном

процессе, но и в инженерной деятельности.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Симонов А.А. Выск Н.Д. Проверка статистических гипотез:

Методические указания и варианты курсовых заданий. Москва, 2005, 46 с.

2. Ю. И. Галанов. Математическая статистика: учебное пособие.

Издательство ТПУ. Москва, 2010, 66 с.

3. Вентцель Е.С. Теория вероятностей: Учебник для студ. вузов, 2005. – 576 с.

4. Э. А. Вуколов, А. В. Ефимов, В.Н. Земсков, А. С. Поспелов. Сборник задач по математике для ВТУЗОВ: Учебник для студентов вузов.

Москва, 2003, 433 с.

5. Чернова Н. И. Математическая статистика: Учеб. пособие / Новосиб. гос. ун-т. Новосибирск, 2007. 148 с.