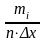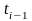Файловый архив студентов. Файловый архив студентов.
1294 вуза, 5024 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Тульский Государственный Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
Михалева kursovoy_po_metrologii.docx
Скачиваний:
4
Добавлен:
14.12.2019
Размер:
838.75 Кб
Скачать
☆
►Содержание►

Задача№4

Найти предельные значения замыкающего размера А при значениях составляющих размеров, полученных в результате решения задачи №3. Расчет произвести вероятностным методом, исходя из допустимого процента брака на сборке, равного 0,27%

Сведем данные для расчета в таблицу

Размер

ξi

ECJ

Tj

αi

αi

Ecj+α

ξ(Ecj+α

| ξ| Tj

(| ξ| Tj)2

А1

29-0,12

-1

-0,060

0,120

+0,2

0,0120

-0,048

0,048

0.120

0.01440

А2

186

-1

0,166

0,290

+0,2

0,0290

EC2+0,029

0,195

0.290

0.03803

А3

29-0,12

-1

-0,060

0,120

+0,2

0,0120

-0,048

0,048

0.120

0.01440

А4

264Js11( 0,016)

+1

0

0,320

0

0

0

0

0.320

0.10240

А5

6h(-0,015)

+1

0,0075

0,015

+0,2

0,0015

0,009

0,009

0.015

0.00225

А6

26Js11( 0.065)

-1

0

0,130

0

0

0

0

0.130

0.01690

  1. Номинальное значение замыкающего размера

NΔ=-29-186-29+264+6-26=0мм

  1. Среднее отклонение замыкающего размера

ЕсΔ=0,048+0,195+0,048+0+0,009+0=+0,3 мм

  1. Допуск замыкающего размера

ТΔ=1,2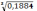 =0,58

  1. Предельные отклонения замыкающего размера

АΔmax=0+0.3+0.5*0.6=0.6

AΔmin=0+0.3-0.5*0.6=0

  1. Сравниваем полученные результаты с заданными

АΔmaxрасч=0,6=АΔmax задан=0,6

АΔmin расч=0=AΔminзадан=0

Следовательно, изменения предельных отклонений составляющих размеров не требуется.

Задача №3

Определить вид ЗРВ по критерию Пирсона;

Записать результат с доверительной вероятностью P=0.97

43,54

43,39

43,44

43,39

43,63

43,53

43,43

43,14

43,55

43,65

43,38

43,55

43,43

43,50

43,39

43,67

43,37

43,54

43,33

43,65

43,54

43,72

43,44

43,42

43,26

43,67

43,55

43,54

43,50

43,34

43,42

43,49

43,42

43,58

43,33

43,52

43,51

43,27

43,26

43,53

43,53

43,59

43,57

43,29

43,47

43,45

43,82

43,41

43,59

43,39

43,44

43,57

43,72

43,44

43,52

43,57

43,27

43,50

43,44

43,68

43,53

43,55

43,68

43,50

43,32

43,45

43,39

43,42

43,60

43,61

43,44

43,39

43,47

43,48

43,57

43,59

43,63

43,66

43,66

43,66

43,46

43,64

43,46

43,78

43,27

43,42

43,43

43,43

43,47

43,60

43,52

43,35

43,28

43,68

43,77

43,50

43,94

43,35

43,51

43,60

Отсортируем исходные данные по возрастанию

Х

43,14

43,26

43,27

43,28

43,29

43,32

43,33

43,34

43,35

43,37

m

1

2

3

1

1

1

2

1

2

1

Х

43,38

43,39

43,41

43,42

43,43

43,44

43,45

43,46

43,47

43,48

m

1

6

1

5

4

6

1

2

4

1

Х

43,49

43,50

43,51

43,52

43,53

43,54

43,55

43,57

43,58

43,59

m

2

5

2

3

4

4

4

3

1

3

Х

43,60

43,61

43,63

43,64

43,65

43,66

43,67

43,68

43,72

43,77

m

3

1

2

1

2

3

2

3

2

1

Х

43,78

43,82

43,94

m

1

1

1

1 Используя полученные данные, найдем значение среднего арифметического Х и оценки среднего квадратического отклонения Sх:

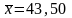
2.С помощью правила «трех сигм» проверяем наличие или отсутствие промахов.

Таким образом, ни один из результатов не выходит за границы интервала 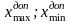 , следовательно, с вероятностью 0.9973 гипотеза об отсутствии грубых погрешностей принимается.

3.Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.

Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разобьем на k одинаковых интервалов .

Принимая k=7, получим

Т.к. в крайние интервалы попадает меньше 5 наблюдений, то объеденим их с соседними.

Результаты производимых вычислений занесем в первую половину таблицы 1, и строим гистограмму.

Из вида гистограммы можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.

Xi-1

Xi

m

Фi-1

Фi

Pi

1

43,05

43,22

1

0.48

-2.86

-0.70

-0.4979

-0.2794

0.2341

2.660

2

43,22

43,26

2

3

43,26

43,38

15

4

43,38

43,51

40

2,92

-0,76

0,06

-0,2794

0,0239

0.2399

1,380

5

43,51

43,64

31

2,38

0,06

0,89

0,0239

0,3133

0,2894

0,035

6

43,64

43,77

14

0.6

0.89

2.80

0.3133

0.4974

0.1841

0.009

7

43,77

43,90

4

4.Проверка нормальности закона распределения по критерию Пирсона.

Т.к. в предыдущем пункте выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используем функцию Лапласа:

В данном случае значения x1 и x2 соответствуют началу и концу интервала. Для каждого из значений нужно рассчитать относительный доверительный интервал 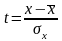, а затем из таблиц функции Лапласа находим соответствующие значения этой функции Ф(t1) Ф(t2).

Найдя, таким образом, значения Pi для каждого интервала ki, заполним соответствующие ячейки таблицы, а затем рассчитаем значение 2 – критерия для каждого интервала.

Суммарное значение 2:4,084

Определим табличное (критическое) значение 2, задавшись доверительной вероятностью 0.97 и вычислив по формуле r=k-3 число степеней свободы:

r=5-3=2

Таким образом, с вероятностью 0.97 гипотеза о нормальности распределения вероятности результата измерения принимается.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности