4. Статистическая сводка и группировка

В результате статистического наблюдения получают большое количество первичных сведений об отдельных единицах изучаемой совокупности. В таком виде материал не характеризует явление в целом. Для проведения анализа его состояния, структуры, динамики и взаимосвязей проводят дальнейшую обработку статистических данных, т.е. переходят ко 2-му этапу статистического исследования - статистической сводке и группировке материала.

Статистическая сводка – это обработка данных статистического наблюдения с целью получения обобщенных характеристик изучаемого социально-экономического явлениям по существенным для него признакам.

Классификация статистической сводки:

1) по глубине обработки информации:

- простая – операция по подсчету общих итогов по совокупности единиц наблюдения

- сложная – включает в себя комплекс операций: группировка статистических данных, подсчет итогов по каждой группе и по всему объекту, представление результатов сводки и группировки в виде статистических таблиц и графиков.

2) по форме обработки информации:

- централизованная – сводка, при которой первичные статистические данные поступают в одну организацию и обрабатываются в ней от начала до конца

- децентрализованная – обработка данных осуществляется последовательными этапами (например, отчеты п/п сводятся территориальными органами субъектов РФ, а затем итоги поступают в ACUC и там определяют итоговые показатели в целом по экономике страны)

3) по технике выполнения:

- автоматизированная

- ручная

Статистическая группировка – это разделение общей совокупности единиц на однородные группы по одному или нескольким существенным признакам.

Признак, по которому производят группировку называется группировочным признаком.

5. Виды группировок и их роль в анализе социально-экономических процессов

Статистические группировки можно разделить по ряду признаков:

1) по характеру решаемых задач:

- типологические – применяют для выявления и характеристики социально-экономических типов явления с их помощью качественно разнородные совокупности разделяют на классы, социально-экономические типы, однородные группы и т.п. (группировка хозяйственных субъектов по форме собственности, организации по видам экономической деятельности)

- структурные – группировки, с помощью которых изучают состав статистической совокупности по величине какого-либо варьирующего признака, определяю показатели, которые в долях (%) выражают удельный вес каждой из выделенных групп. (структура потребительских расходов)

- аналитические – применяют для исследования взаимосвязей между признаками изучаемых явлений. При их построении из 2-х взаимосвязанных показателей один выступает как фактор, т.е. влияющий на другой, а второй как результат влияния первого. При построении аналитической группировки статистическую совокупность разделяют на группы по факторному признаку. (например, влияние ОПФ на выпуск продукции )

2) по способу построения:

- простые – группы образованы по 1 признаку

- сложные – группы образованы по нескольким признакам (бывают комбинированные и комбинационные)

3) в зависимости от исходного материала:

- первичные – выполняются на основе первичного статистического материала

- вторичные – ранее проведенные группировки с различными интервалами приводят к единому сопоставимому виду, т.е. производят перегруппировку.

Перегруппировку можно произвести 2-мя способами:

- объединить мелкие группы в более крупные

- закрепить за каждой группой определенную долю единиц совокупности

Метод группировки применяют для решения следующих задач:

- выделение социально-экономических типов явлений

- изучение структуры явления

- выявление взаимосвязи между отдельными признаками явления.

6. Методика построения аналитической группировки. Определение числа групп

Проведение статистических группировок связано с последовательным решением следующих задач:

* выбор группировочного признака – признак должен быть существенным; чаще всего и удобнее в качестве группировочного признака берут факторный признак.

* построить ранжированный ряд по группировочному признаку

* определить число групп – можно 2-мя способами:

- согласно методическим указаний, если число наблюдений до 40, то выделяют 3 группы.

- по формуле: , где N – число наблюдений

* определить шаг интервала, который разделяет одну группу от другой

- максимальное значение группировочного признака

- минимальное значение группировочного признака

n – число групп * определить границы групп

1 группа: до

2 группа: до …. * в группах провести статистическую сводку показателей, охарактеризовать каждую группу и совокупность в целом * сделать обобщающие выводы

7. Статистические ряды распределения, их виды. Основные характеристики

Составной частью сводной обработки данных статистического наблюдения является построение рядов распределения.

Ряд распределения – это группировка единиц совокупности по величине какого-либо варьирующего признака.

(распределение студентов по успеваемости)

Цель построения рядов распределения – выявление основных свойств и закономерностей исследуемой статистической совокупности.

Ряды распределения, построенные по качественным признакам, называются атрибутивными (население по полу). Ряды распределения, построенные по количественным признакам, называются вариационными (население по возрасту).

Вариационные ряды состоят из вариант (х) и частот (f)

Если варианты заданы целыми числами, то ряд называется дискретным. Если варианты заданы интервалами, то ряд называется интервальным.

Для построения дискретного ряда с небольшим числом вариант достаточно перечислить все встречающие варианты – значения признака Х, а затем подсчитать частоту повторения каждого варианта. В том случае, когда число вариантов дискретного ряда достаточно велико, а также при анализе вариаций непрерывного признака, когда значение признака отдельных единиц могут вообще не повторяться, строят интервальный ряд распределения.

Порядок построения интервального ряда распределения

1) построить ранжированный ряд

2) определить количество групп по формуле

, где N – число наблюдений

3) определить шаг интервала

- максимальное значение группировочного признака

- минимальное значение группировочного признака

n – число групп

4) определить границы интервалов

1 группа: до

2 группа: до …

5) подсчитать количество единиц в каждом интервале и построить итоговую таблицу – интервальный ряд распределения.

Для большей наглядности ряды распределения изображают графически. Графическое изображение рядов распределения облегчает их анализ и позволяет судить о форме распределения. Дискретный ряд изображают графически в виде полигона. Для его построения по оси ОХ отражают значение признака, а по оси ординат ОУ – частоты.

Интервальный ряд изображают графически в виде гистограммы. Она состоит из прямоугольников, основаниями которых являются нижняя и верхняя граница интервалов, а высота соответствует частоте интервала. Также можно построить кумуляту распределения.

Статистические характеристики ряда распределения можно подразделить:

* показатели вариации (размах вариации, среднее квадратическое отклонение, дисперсия, среднее линейное отклонение, коэффициент вариации)

* показатели центра распределения: мода и медиана

* показатели форм распределения

Предельная кривая, к которой стремится всякое статистическое распределение называется кривой распределения.

Распределение может быть: многовершинное и одновершинное

Многовершинность свидетельствует о неоднородности изучаемой совокупности. Среди одновершинных распределений наиболее характерными являются: симметричные (в них частоты по обе стороны от центра уменьшаются равномерно) и умеренно асимметричные (в них частота по одну сторону от вершины распределения снижается быстрее, чем по другую) бывает правосторонняя асимметрия и левосторонняя асимметрия.

Асимметрию можно измерить по формуле:

Если – симметричное распределение

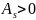- правосторонняя асимметрия

- левосторонняя асимметрия

Если - правосторонняя асимметрия

- левосторонняя асимметрия

По сравнению с нормальным распределением, исходное распределение может быть высоко вершинным и низко вершинным.

Степень остро вершинности или эксцесс измеряют по формуле

Если – нормальное распределение

– высоко вершинное распределение

– низко вершинное распределение