атомка-1 / Шпоры по атомке (59,62,63,65,68,69(29), каталог)

68) Радиоактивность. Радиоактивностью называется самопроизвольный распад ядер с испусканием одной или нескольких частиц. Радиоактивное ядро называется материнским, а образовавшиеся ядра - дочерними. Необходимое условие радиоактивного распада – масса исходного ядра должно быть больше суммы масс продуктов реакции. Поэтому каждый распад идёт с выделением энергии.Основной закон радиоактивности. Одинаковые ядра претерпевают распад за различное время, предсказать которое для каждого ядра в отдельности заранее нельзя. Однако можно установить закон общий для совокупности ядер. Для этого будем считать, что число ядер распадающихся за промежуток времени dt, пропорционально как числу N ядер в данный момент времени, так и самому промежутку времени: (10)где - константа пропорциональности (постоянная распада), для каждого вещества своя.Интегрирование уравнения даёт: (11), где N_o – число ядер в момент t=0, N – число нераспавшихся ядер. Самостоятельно найти функцию плотности вероятности (и нормировать её), период полураспада Т, среднее время жизни .Основные виды радиоактивности. Альфа-распад - самопроизвольное испускание ядром -частиц по схеме: (12)Установлено, что -частицы испускают только тяжёлые ядра. Кинетическая энергия -частицы несколько МэВ. В воздухе они пролетают несколько сантиметров. Их энергия расходуется на образование ионов вдоль пути. Дочернее ядро после распада может оказаться в возбужденном состоянии, поэтому после -распада может последовать испускание -квантов. Покидая ядро -частица преодолевает потенциальный барьер, высота которого превышает её энергию (рис.3). Преодоление этого барьера происходит благодаря туннельному эффекту. Соответствующий расчет хорошо подтверждается результатами измерений. Бета-распад – самопроизвольный процесс при котором ядро превращается в другое ядро с тем же массовым числом А, но другим зарядом, отличающимся от исходного на . Бета-распад сопровождается испусканием или захватом электрона.Различают три вида -распада: 1. электронный -распад, при котором ядро испускает электрон и зарядовое число ядра становится Z+1. 2. позитронный -распад, при котором ядро испускает позитрон и его заряд становится Z-1. 3.К-захват, в котором ядро захватывает один из электронов электронной оболочки атома (обычно из К-оболочки). Освободившееся место занимают электроны выше лежащих оболочек, поэтому он сопровождается рентгеновским излучением. При исследованиях -распада выяснилось, что - спектр содержит только 1/3 энергии распада. Нужно было либо найти куда исчезает энергия, либо признать, что закон сохранения энергии не выполняется. Проблему решил Паули. Он предположил, что вместе с электроном испускается электрически нейтральная частица, неуловимая вследствие большой проникающей способности. Он назвал её нейтрино, что значит «маленький нейтрончик». Ещё одним обстоятельством в пользу нейтрино была необходимость сохранения момента импульса. Если бы нейтрон распадался бы только как

, то суммарный спин родившихся частиц был бы 1, либо 0, в то время как спин нейтрона ½ . Таким образом, спин нейтрино должен быть ½ или 3/2 . Сейчас установлено что ½ . Итак, схемы -распада таковы:

Экспериментально установлено, что существует шесть видов нейтрино: Гамма-распад – заключается в испускании возбуждённым ядром -квантов при переходе в основное состояние. Энергия -квантов варьируется от 10 кэВ до 5 МэВ. Спектр испускания дискретный. Также возбуждённое ядро может перейти в основное состояние, передав энергию одному из атомных электронов, например К-электрону. Этот процесс называют внутренней конверсией электронов. Он сопровождается рентгеновским излучением.

6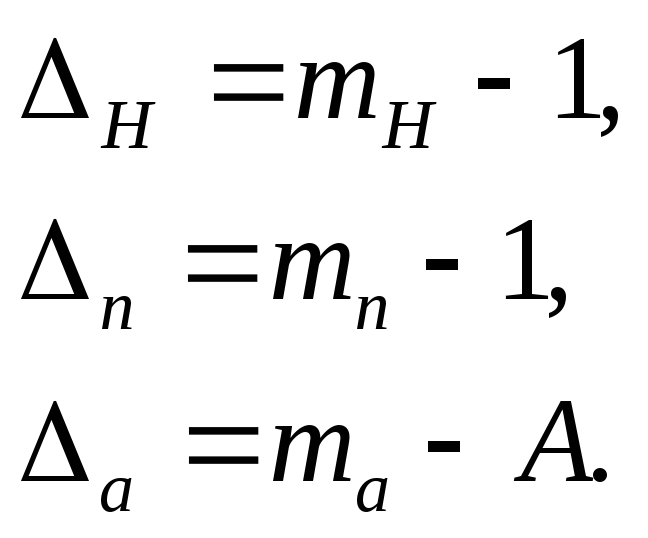3) Оболочечная и капельная модели ядер. Так как последовательной теории ядра до сих пор нет, то для описания процессов и явлений используют модели. Капельная модель. Предложена Борном в 1936г. В ней атомное ядро рассматривается как капля заряженной несжимаемой жидкости. С её помощью удалось объяснить процесс деления ядра и вывести полуэмпирическую формулу для энергии связи ядра. Оболочечная модель. Предложена Геперт – Майером и Йенсоном в 1950г. В этой модели каждый нуклон движется в усреднённом поле остальных нуклонов ядра. Имеются дискретные энергетические уровни, заполненные с учетом принципа Паули. Эти уровни группируются в оболочки, в каждой из которых может находиться определённое число нуклонов. Полностью заполненные оболочки являются особо устойчивыми структурами. Таковыми являются ядра, имеющие число протонов или нейтронов 2, 8, 20, 50, 82, 126. Эти числа называются магическими. Кроме того, эта модель позволяет объяснить спины основных и возбуждённых состояний ядер, а также их магнитные моменты. Масса и энергия связи ядра. Масса ядра не является аддитивной величиной: она не равна сумме масс образующих ядро нуклонов. Причиной является взаимодействие нуклонов в ядре. Из-за этого для того, что бы разделить ядро на отдельные свободные нуклоны необходимо совершить работу, которая определяет энергию связи ядра E_св. И наоборот, при образовании ядра из свободных нуклонов эта энергия выделяется (например, в виде электромагнитного излучения).Скорость света отсутствует в формуле, так как массы выражены в энергетических единицах. Более детально формулу можно записать так: (2)Эта формула неудобна для расчетов, так как в таблицах приведены значения масс атомов, а не ядер. Поэтому заменим массу протона массой атома водорода, а массу ядра массой атома. Другими словами добавим и вычтем из формулы одно и тоже число электронов. Тогда формула примет вид: (3). Также для упрощения расчетов вводят понятие дефект массы как разность между массой в а.е.м. и массовым числом А ядра или нуклона :(4)Тогда формула примет вид:Размер ядер. У атомного ядра нет четко определённой границы. Из кспериментов по рассеянию установлено, что концентрация n нуклонов от радиуса величина постоянная (рис.1).

В первом приближении ядро можно считать сферическим

(1)где.

Следовательно, масса ядра пропорциональна его объёму

.Плотность вещества во всех ядрах примерно одинакова и равна - величина очень большая.

59) Модель свободных электронов в металле. Валентные электроны в металле могут почти свободно перемещаться. Они обуславливают электропроводность металла, и по этой причине их называют электронами проводимости.

Рассмотрим образец металла (для простоты кубической формы со стороной L). Запишем уравнение Шрёдингера свободного электрона: (1)

Его решением будет функция(2)

Энергия электрона равна(3): Нормируем пси-функцию

(4),где L³ объём образца. Теперь функция имеет вид(5):

Пси-функция должна удовлетворять граничным условиям, которые заключаются в требовании, чтобы она была периодической по x, y, z с периодом L. Она будет удовлетворять этим условиям при волновом векторе с компонентами:(6)

где -целые числа принимающие независимо друг от друга значения . Подставим в (5) и получим: (7) Замена на , либо на , либо на оставляет функцию без изменений. Так как значения волнового вектора квантуются, то квантуются и значения энергии электрона проводимости в металле. Подстановка (6) в формулу для энергии (3) даёт: (8)Состояние электрона проводимости можно задать четырьмя квантовыми числами , где - спиновое квантовое число. Уровни энергии являются вырожденными, так как одной и той же энергии соответствует несколько комбинаций квантовых чисел. Для уровня Е₂ кратность вырождения равна 24. Таким образом, с ростом энергии кратность вырождения растёт. Число состояний в интервале энергий. Определим число квантовых состояний (фазовых ячеек) dZ для свободных электронов с энергиями в интервале . Выразим импульс через энергию и продифференцируем . Воспользуемся формулой (10) и лекции 13:,(9)где.Зависимость числа состояний от энергии дана на рисунке 1. Чтобы определить число свободных электронов в интервале энергий нужно умножить dZ на функцию заполнения: (10)

где 2 поставлена в формуле (10) в связи с тем, что в каждой фазовой ячейке могут расположиться два электрона с противоположно направленными спинами.

62) Виды взаимодействия и классы элементарных частиц. Под элементарными частицами понимают такие мик­рочастицы, внутреннюю структуру которых на современ­ном уровне развития физики нельзя представить как объединение других частиц. Во всех наблюдавшихся до сих пор явлениях каждая такая частица ведет себя как единое целое.В настоящее время известны четыре вида взаимо­действий между элементарными частицами: сильное¹), электромагнитное, слабое и гравитационное (мы пере­числили их в порядке убывания интенсивности).

Сильное взаимодействие. Этот вид взаимодействия называют иначе ядерным, так как оно обеспечивает связь нуклонов в ядре (см. § 89). Интенсивность взаи­модействия принято характеризовать безразмерной кон­стантой взаимодействия G². Эта же констан­та характеризует вероятность процессов, обусловленных данным взаимодействием. Для сильных взаимодействий G²=Gs²=1. Наибольшее расстояние, на котором про­является сильное взаимодействие (радиус действия г), составляет, как мы знаем, примерно 10^-13 см. Частица, пролетающая со скоростью, близкой к с, в непосред­ственной близости к другой частице, будет взаимодей­ствовать с ней в течение времени т = r/с ~ 10^-13/(З*10¹⁰) ~ 10^-23 сек. В соответствии с этим говорят, что сильное взаимодействие характеризуется временем взаимодействия т₈ порядка 10^-23 сек.

Электромагнитное взаимодействие. Радиус действия электромагнитного взаимодействия не ограничен (г = = оо). Константа взаимодействия равна G²=Ge²=e²/(hc)=1.137. Следовательно, интенсивность электромагнитного взаи­модействия примерно в 100 раз меньше, чем сильного. Время, необходимое для того, чтобы проявилось взаи­модействие, обратно пропорционально его интенсивности (или вероятности). Поэтому для электромагнитного взаимодействия - Te~10^-21 сек.

Слабое взаимодействие. Слабое или распадное вза­имодействие ответственно за все виды B-распадов ядер (включая K-захват), за многие распады элементарных частиц, а также за все процессы взаимодействия ней­трино с веществом. Слабое взаимодействие, как и силь­ное, является короткодействующим. Константа взаимо­действия G² равна 10^-14. Следовательно, время взаимодействия Tw ~ 10^-9 сек.

Гравитационное взаимодействие. Радиус действия не ограничен (г = бесконечно). Константа взаимодействия крайне мала: G² = 10^-14. Соответственно время взаимодей­ствия составляет Tg ~ 10⁹ лет. Гравитационное взаимо­действие является универсальным, ему подвержены все без исключения элементарные частицы. Однако в про­цессах микромира гравитационное взаимодействие ощу­тимой роли не играет. В соответствии с характером взаимодействий, в ко­торых они способны участвовать, элементарные частицы делятся на 3 класса.

1. Фотоны, у (кванты электромагнитного поля). Эти частицы участвуют в электромагнитных взаимодействиях, но не обладают сильным и слабым взаимодействиями. 2.Лептоны (греческое «лептос» означает легкий). К их числу относятся частицы, не обладающие сильным взаимодействием: мюоны (+), электроны (е-, е+) и нейтрино (v, v^~). Все лептоны имеют спин, равный ½. Такие частицы подчиняются статистике Ферми — Дирака (учитывающей принцип Паули), вследствие чего называются фермионами. Все лептоны обла­дают слабым взаимодействием. Те из них, которые имеют электрический заряд (т. е. мюоны и электроны), обладают также электромагнитным взаимодействием.

3. Адроны (греческое «адрос» означает крупный, массивный). Этот класс включает в себя все сильно взаимодействующие частицы. Наряду с сильным эти частицы обладают также слабым и электромагнитным взаимодействиями. Адроны подразделяются на две под­группы: мезоны и барионы.

Мезоны — сильно взаимодействующие нестабильные частицы, не несущие так называемого барионного за­ряда (см. ниже). К их числу принадлежат -мезоны (⁺,^-,⁰) и K-мезоны, или каоны (К⁺, К^-, К⁰, K°^~). Масса K-мезонов составляет ~970т_е (494 Мэв для заряженных и 498 Мэв для ней­тральных K-мезонов). Время жизни K-мезонов имеет ве­личину порядка 10^-8 сек. Они распадаются с образо­ванием -мезонов и лептонов или только лептонов. За­ряженные -мезоны распадаются с образованием лептонов; °-мезон распадается пре­имущественно с образованием у-фотонов. Распад мезо­нов (за исключением °-мезона) идет за счет слабого взаимодействия, вследствие чего они отличаются вре­менами жизни (~10^-8 сек), значительно превышаю­щими ядерные времена. Распад °-мезона на у-фотоны определяется не слабым, а электромагнитным взаимо­действием (фотоны в слабых взаимодействиях не участ­вуют) . В соответствии с этим время жизни °-мезона (~10^-16 сек) на много порядков меньше, чем времена жизни остальных мезонов. В отличие от лептонов ме­зоны обладают не только слабым (и, если они заря­жены, электромагнитным), но также и сильным взаимо­действием, проявляющимся при взаимодействии их меж­ду собой, а также при взаимодействии между мезонами и барионами. Спин всех мезонов равен нулю, так что принцип Паули на них не распространяется. Частицы с целым (или нулевым) спином подчиняются статис­тике Бозе — Эйнштейна, в связи с чем носят на­звание бозонов.

Подгруппа барионов объединяет в себе нуклоны (р, п) и нестабильные частицы с массой, большей мас­сы нуклонов, получившие название гиперонов (°, ⁺, °, ^-, °, ^, ^). Все барионы обладают силь­ным взаимодействием и, следовательно, активно взаимо­действуют с атомными ядрами. Спин всех барионов равен 1/2, так что барионы являются фермионами. За исключением протона, все барионы нестабильны. При распаде бариона, наряду с другими частицами, обяза­тельно образуется барион. Эта закономерность является одним из проявлений закона сохранения барионного заряда. В последнее время обнаружено около 70 короткоживущих частиц, которые получили название резонансов. Эти частицы представляют собой резонансные со­стояния, образованные двумя или большим числом эле­ментарных частиц. Время жизни резонансов составляет всего лишь 10^-23 - 10^-22 сек. Это указывает на то, что распад резонансов происходит за счет сильного взаимо­действия. Распад других частиц осуществляется за счет слабого (иногда электромагнитного) взаимодействия. Поэтому времена жизни их значительно больше. Некоторые из резонансов являются бозонами и дол­жны быть отнесены к классу мезонов. Таковы, напри­мер, -резонанс (или -мезон), распадающийся на три -мезона, или К*-резонанс (K*-мезон), распадающийся на K-мезон и -мезон. Другие резонансы — фермионы и должны быть причислены к классу гиперонов. Примером может служить *-резонанс (*-гиперон), распа­дающийся на -гиперон и -мезон.

69) Элеме-ные частицы. Законы сохра-ния. Систематик.

Закон сохранения	сил	э/м	слаб
Энергии E Импульса р Момента импул. (спина) М Электр. Заряда Q………… ,Барионного заряда В Лептонного заряда L……… Изотопического спина Т Гиперзаряда У (стран.) Зарядового сопряжения. С Чётности Р………………… Комбиниров.чётности СР	+ + + + + + + + + + +	+ + + + + + -- + + + +	+ + + + + + -- -- -- -- --

Каждый закон сохранения выражает определенную симметрию системы. Законы сохранения импульса р, момента импульса М и энергии Е отражают свойства симметрии пространства и времени: сохранение энергии есть следствие однородности времени, сохранение р об­условлено однородностью пространства, а сохранение М — его изотропностью. Закон сохранения четности свя­зан с симметрией между правым и левым (Р-инвариант-ность). Симметрия относительно зарядового сопряжения (симметрия частиц и античастиц) приводит к сохране­нию зарядовой четности (С-инвариантность). Законы сохранения электрического, барионного и лептоиного за­рядов выражают особую симметрию волновой функции. Наконец, закон сохранения изотопического спина отра­жает изотропность изотопического (зарядового) про­странства. Несоблюдение одного из законов сохранения означает нарушение в данном взаимодействии соответ­ствующего вида симметрии. Например, электромагнитное взаимодействие нарушает симметрию изотопического пространства, вследствие чего изотопический спин Т не сохраняется в электромагнитных взаимодействиях. Теории унитар­ной симметрии элементарных частиц. В этой тео­рии предполагается, что сильное взаимодействие инва­риантно относительно специальных преобразований') в некотором трехмерном комплексном векторном простран­стве (пространстве унитарного спина), которые сохраняют неизменным изотопический спин Т и гипер­заряд У. Таким способом удается сгруппировать заря­довые мультиплеты в супермультиплеты (или унитарные мультиплеты). Частицы²), состав­ляющие супермультиплет, должны иметь одинаковые спин и четность Р. Они могут отличаться по массе, элек­трическому заряду, гиперзаряду и изотопическому спину, однако эти величины должны быть связаны между со­бой определенными правилами. Систему симметрии частиц, устанавливаемую уни­тарной теорией, называют также восьмеричным путем, поскольку в ней производятся действия над восемью квантовыми числами. На рис. 279 изображен октет (супермультиплет, включающий 8 частиц), объединяющий нуклоны (n, р) и A-, -, -гипероны. Все они имеют спин 1/2 и положи­тельную четность. Справа приведена масса частиц (в Мэв), внизу — электрический заряд Q, слева —значе­ния гиперзаряда Y и изотопич. спина Т.

65) Понятие о кварках. Так называемых элементарных частиц стало так мно­го (вместе с резонансами более ста), что возникли серьезные сомнения в их элементарности. Каждая из сильно взаимодействующих частиц характеризуется тремя независимыми аддитивными квантовыми числами: зарядом Q, гиперзарядом У и барионным зарядом В. В связи с этим появилась гипотеза о том, что все ча­стицы построены из трех фундаментальных частиц — носителей этих зарядов. Первая модель подобного рода была предложена японским физиком С. Саката, кото­рый считал фундаментальными частицами протон р, ней­трон п и A°-гиперон²). Однако схема Саката оказалась неприменимой в области сильных взаимодействий. Гелл-Манн и Цвейг ввели в рассмотрение гипотетиче­ские частицы, получившие название кварков³). Этим частицам приписываются дробные квантовые числа, в частности электрический заряд, равный -1/3, -1/3 и + 2/3 соответственно для каждого из трех кварков, они обозначаются буквами u, d и s (странность равна -1, у остальных 0); барионные числа равны +1/3, спины = 1/2, также для каждого кварка существует антикварк. Каждому кварку приписывается одинаковый магнитный момент. Они имеют жел, син, кр цвета, антикварки соотв-но фиол, оран, зел, которые в основном определяют различие во взаимном притяжении и отталкивании. Затем появились: 4-й кварк – c, очарование = 1 (у остальных = 0), 5-й – b (который был нужен для объяснения свойств открытой частицы (ипсилон)), 6-й – t - очень массивный кварк. Мезоны образуются из пары кварк-антикварк, а барионы – из трёх кварков. Идея кварков оказалась весьма плодотворной. Она позволила не только систематизировать уже известные частицы, но и предсказать целый ряд новых. В частности существование омега-минус-гиперона и его свойства. Ряд экспериментальных данных указывает с несомненностью на реальное существование кварков. К их числу относятся рез-ты изучения рассеяния быстрых электронов протонами.

1) Тепловое излучение и его характеристики.

2) Испускательная и поглощат. способ-сти. Закон Кирхгофа

3) Формула Релея-Джинса.

4) Связь плотности энергии со светимостью черного тела.

6) Стоячие волны в 3-ёхмерном резонаторе.

7) Число волн в интервале частот

8) Закон Стефана-Больцмана и смещение Вина.

9) Фотоэффект.

10) Опыт Столетова и Милликенапо фотоэффекту.

11) Опыт Франка Герца.

12) Опыт Боте. Фотоны.

13) Эффект Комптона

14) Тормозное рентгеновское излучение.

15) Формула Планка.

16) Вывод закона Стефана-Больцмана из формулы Планка.

17) Теория Бора атома водорода.

18) Вывод обобщенной формулы Бальмера

19) Схема уровней энергии в спектральные серии атома Н. 20) Опыт по рассеянию A-частиц. Формула Резерфорда.

21) Частица в глубокой потенциальной яме.

22) Гипотеза Де-Бройля.

23) Физический смысл и свойства пcu-функдии.

24) Собственный механ- и магнитные момент е.

25) Постулаты Бора. Опыт Франка и Герца.

26) --> 69)Законы сохранения для элементарных частиц

27) Соот-ние неопред. Гейзенберга.Оценка миним. энергии.

28) Соот-ние неопред. Гейзенберга. Одна и две щели.

29) Статистич. среднее значение энергии осциллятора.

30) Квантование орбитального момента импульса.

31. Соот-ние неопред. Гейзенберга. Оценка размер.атома.

32) Уравнение Шрёдингера. Свойства пси-функции.

33) Резуль-ты квантовой механики для Н-подобного атома.

34) Прохождение частицы через потенциальный барьер.

35) Квантование проекции момента импульса.

36) Принцип Паули. Заполнение электронных оболочек.

37) L-S и J-J связи электронов в атоме. Правило Хунда.

38) Результаты квантовой механики дли атома водорода.

39) Результирующий момент многоэлекгронного атома.

40) Тонкая структура линий спектра атома водорода.

41) Спектралъние спектры щелочных элементов.

42) Результаты квантовой механики для осциллятора.

43) Схема энергетических уровней 2-ухатомноймолекулы.

44) Колебательно-вращательные полосы

45) Врашат. полосы спектра гомоядерной молекулы.

46) Характеристика рентгеновского спектра.

47) Тонкая структура линий хар-ческого рентг. спектра.

48) Эффект Зеемана.

49) Эффект Пашена-Бака.

50) Эффект Штарка.

51) Спонтанное и вынужд. излучение. Коэф-ты Эйнштейна. 52) Излучение лазеров и его свойства. Рубиновый лазер.

53) Теплоемкость кристалл. решетки. Модель Эйнштейна.

54) Теплоемкость кристаллической решетки Модель Дебая.

55) Распределение Бозе-Эйнштейна. Фононы.

56) Распределение Ферми-Дирака.

57) Клас. и квант. выражения для энергии колебаний крист

58) Энергетические зоны в кристалла. Диэлектрики….

59) Модель свободный электронов. Число состояний.

60) Электронный парамагнитный резонанс.

61) Собственные и примесные полупроводники.

62) Виды взаимодействия и классы элементарных частиц.

63) Оболочечная и капельная модели ядра.

64) Состав атомного ядра. Изо-разновидности ядер атомов.