1.5 Экспоненциальное (показательное) распределение.

Экспоненциальное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события. Чаще всего данное распределение используется в задачах, где требуется определить вероятность того, что событие произойдет раньше/позже среднестатистического времени происхождения данного события. Задается показательное распределение уравнением: , где - параметр, равный .

Таким образом, математическое ожидание равняется среднему времени между событиями, т.е. , дисперсия же равна . График распределения выглядит так:

О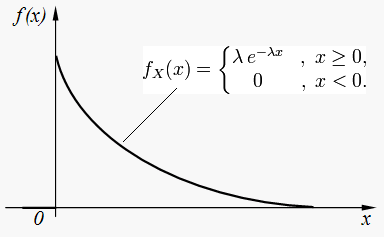 тсюда можно сделать вывод, что вероятность промежутка Х, т.е. P(x>u), будет находиться через интеграл. Однако опуская все доказательства, можно представить 3 формулы:

1. 

2. 

3. 

4. 

Примечание: последняя формула получается, если хорошо взглянуть на график и знать, что вероятность – это площадь:

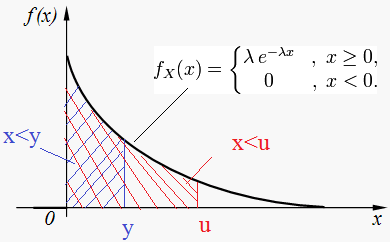
Решим задачу:

Время безотказной работы мобильного телефона фирмы имеет показательное распределение. Средний срок службы телефона составляет 2 года. Какова вероятность, что телефон выйдет из срока в течение года эксплуатации? Какова вероятность, что телефон проработает меньше 6 лет, если он уже проработал больше 4 лет?

Итак, На первый вопрос ответим, используя формулы, приведенные выше: . На второй вопрос ответим также, но учитывая, что это условная вероятность: .

Ответ: ; .

1.6 Пуассоновское распределение.

Распределение Пуассона чаще всего используется в задачах, где нужно установить вероятность того, что за среднестатистическое время произойдет фиксированное число событий, но может использоваться в принципе в любых задачах, где нужно найти вероятность события, при условии, что это событие крайне редкое, но неоднократное (как поломка водопровода). Задается распределение уравнением . Как и в случае с показательным распределением = . Математическое ожидание также равняется , однако дисперсия теперь равна . Вероятность высчитывается по формуле: . Кроме того, применяется также формула , она используется, когда требуется найти число событий не за единицу времени, а за определенный промежуток времени t.

Решим задачу:

Среднее число вызовов, поступающих на АТС за 1 мин, равно двум. Найти вероятность того, что за 4 мин. поступит: а) три вызова; б)менее трёх вызовов; в)не менее трёх вызовов.

Решение:

Итак, имеем, что =2, а t=4, тогда:

1. 

2. 

.

3. . Стоит отметить, что вместо того, чтобы складывать , гораздо легче использовать сразу .

Ответ: ; ; .

Глава IV. Формулы полного распределения и Байеса

Рассмотрим следующую задачу:

На фабрике, производящей элементы космических аппаратов, первая установка производит 45%, вторая – 55% всех изделий, причем в их продукции брак составляет соответственно 3%, 6%. а) Найдите вероятность того, что случайно выбранное изделие, изготовленное на этой фабрике, является бракованным; б) найдите вероятность того, что это изделие произведено второй установкой.

Для решения поставленной задачи требуется использовать 2 формулы:

1. Формулу полной вероятности:

2. Формулу Байеса:

Дано:

Событие А_к – изготовление деталей к-ым аппаратом

Событие В – изготовление бракованной детали

P(A₁)=0,45 –доля изготовленных деталей первым аппаратом

P(A₂)=0,55 – доля изготовленных деталей вторым аппаратом

P(В|A₁)=0,03 – доля брака, среди деталей, изготовленных первым аппаратом

P(В|A₂)=0,06 – доля брака, среди деталей, изготовленных вторым аппаратом

Решение:

А) Для ответа на первый вопрос нам необходимо найти сумму двух вероятностей: что изделие окажется бракованным и будет изготовлено первым аппаратом и что изделие окажется бракованным и будет изготовлено вторым аппаратом:

Р(брака)=Р(В)= ∑Р(А_к)*Р(В|А_к)= Р(А₁)*Р(В|А₁) + Р(А₂)*Р(В|А₂) = 0,45*0,03 + 0,55*0,06=0,0465= 4,65%.

Ответ: Вероятность того, что случайно выбранное изделия окажется бракованным составляет 4,65%.

Б) Переводя вопрос на язык математики, нам необходимо найти P(A₂|В).

Прежде всего, стоит отметить, что у нас уже есть P(В|A₂). Разница в том, что P(В|A₂) – вероятность того, что случайное изделие, произведенное вторым аппаратом, – бракованное, а P(A₂|В) – вероятность того, что случайно выбранное бракованное изделие было изготовлено вторым аппаратом.

Таким образом, используя формулу Байеса, получим: = = 0,7097 ≈ 71%

Ответ: Вероятность того, что бракованное изделие было произведено вторым аппаратом составляет 71%.