
- •Карточка. Тервер.
- •2 Курс.
- •Оглавление.
- •Глава I. Основные определения и обозначения.
- •Базовые обозначения
- •Пересечение. Объединение. Независимость.
- •Глава II. Характеристики случайной величины.
- •Глава III. Распределения
- •3.1 Равномерное распределение
- •3.2Дискретное распределение. Таблица.
- •1.3Нормальное распределение.
- •1.4Биномиальное распределение.
- •1.5 Экспоненциальное (показательное) распределение.
- •1.6 Пуассоновское распределение.
- •Глава IV. Формулы полного распределения и Байеса
3.2Дискретное распределение. Таблица.
xk |
-2 |
1 |
2 |
5 |
pk |
3/8 |
2/8 |
2/8 |
1/8 |
Если по условию нам дана такая таблица, то решим наиболее типичные задания для нее:
M[x] - ?
Мат.
ожидание находится по общей формуле:
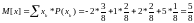 .
Ответ:
.
Ответ:
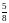 .
.
D[x] - ?
Дисперсия
также находится по общей формуле:
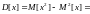
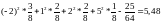 .
Ответ: 5,48.
.
Ответ: 5,48.
P(1< X < 6) - ?
P(1
< X
< 6) = P(2)+P(5)=
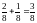 .
Ответ:
.
Ответ:
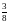 .
.
P( X > 5 | X > 3) - ?
P(
X
> 5 | X
> 3) =
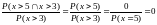 .
Ответ: 0.
.
Ответ: 0.
Примечание: в последних двух примерах мы находили вероятности, учитывая только данные таблицы, т.е. неравенству 1 < X < 6, удовлетворяют лишь два Х из таблицы (2 и 5), поэтому мы и находим P(1< X < 6) как сумму вероятностей подходящих иксов.
1.3Нормальное распределение.
Нормальное распределение хорошо объясняется с помощью графика:
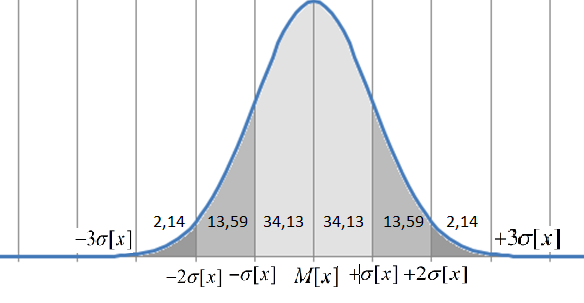
То
есть, вероятность того, что переменная
Х будет лежать на отрезке от M[x]
до
 равна 34,13 %. Вероятность того, что
переменная Х будет больше M[x]
равна 50%. Площадь всего графика равна
равна 34,13 %. Вероятность того, что
переменная Х будет больше M[x]
равна 50%. Площадь всего графика равна
 ,
т.е. 1 или 100%.
,
т.е. 1 или 100%.
В
задаче обычно нормальное распределение
задается формулой:
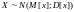 .
Если задача текстовая, то стоит посмотреть:
если она не имеет никаких особенностей,
присущих другим распределениям, то
перед нами – нормальное распределение.
.
Если задача текстовая, то стоит посмотреть:
если она не имеет никаких особенностей,
присущих другим распределениям, то
перед нами – нормальное распределение.
Пример:
 .
Из условия видно, что M[x]=5,
=2.
Построим график:
.
Из условия видно, что M[x]=5,
=2.
Построим график:

И ответим на вопросы:
M[2X+5] - ?
M[2X+5]=2* M[x]+5=15. Ответ: 15.
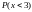 -
?
-
?
= 13,59%+2,14%=15,73%. Ответ: 15,73%.
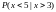 -
?
-
?
=
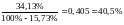 .
Ответ: 40,5%.
.
Ответ: 40,5%.
Теперь решим текстовую задачу:
Среднее значение и стандартное отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найти вероятность того, что в результате трех испытаний одно из полученных значений Х не попадет в интервал (15, 25).
Решение:
Построим график:
С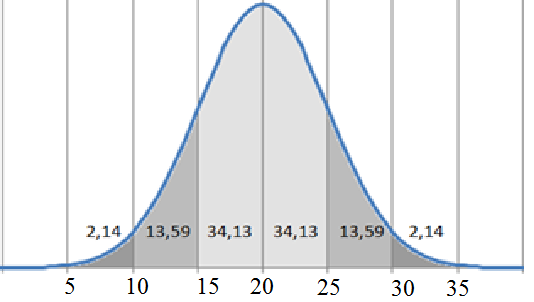 обытие,
что при 3-х экспериментах одно из значений
Х не попадет в промежуток, представляет
собой пересечение 3-х событий: значение
Х попадет в интервал в 2-х случаях и не
попадет в одном. Существует 3 подобных
комбинации:
обытие,
что при 3-х экспериментах одно из значений
Х не попадет в промежуток, представляет
собой пересечение 3-х событий: значение
Х попадет в интервал в 2-х случаях и не
попадет в одном. Существует 3 подобных
комбинации:
А: Х попадает, Х попадает, Х не попадает.
В: Х попадает, Хне попадает, Х попадает.
С: Х не попадает, Х попадает, Х попадает.
Найдем искомую вероятность как сумму вероятностей трех вышеперечисленных событий:
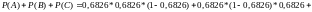

Ответ: 44%
1.4Биномиальное распределение.
Биномиальное
распределение применимо в задачах, где
у нас существует лишь два исхода: выигрыш
или проигрыш, орел или решка и т.д..
Задается данное распределение записью:
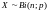 ,
где n
– количество проведенных экспериментов,
p
– вероятность благоприятного исхода.
Следует заметить, что математическое
ожидание и дисперсию в подобных задачах
можно найти по упрощенным формулам:
,
где n
– количество проведенных экспериментов,
p
– вероятность благоприятного исхода.
Следует заметить, что математическое
ожидание и дисперсию в подобных задачах
можно найти по упрощенным формулам:
 ,
,
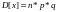 ,
где q
– вероятность неблагоприятного исхода,
которая равна q=1-p
,
где q
– вероятность неблагоприятного исхода,
которая равна q=1-p
Вероятность при биномиальном распределении находится по формуле Бернулли:
 ,
где m
– количество благоприятных исходов, а
,
где m
– количество благоприятных исходов, а
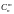 - число сочетаний из n
по m,
т.е. количество комбинаций m
элементов, которые берутся из n
элементов без повторений. Зная, что
- число сочетаний из n
по m,
т.е. количество комбинаций m
элементов, которые берутся из n
элементов без повторений. Зная, что
 ,
формула Бернулли принимает вид:
,
формула Бернулли принимает вид:
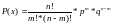 .
.
Рассмотрим
наиболее типичные примеры на основе
распределения X Bi(8;
0,25); Y=
X+2
Bi(8;
0,25); Y=
X+2
Найти: M[Y], P(X=1), P(Y < 3), P(X < 3 | X > 0)
Решение:
M[Y]=M[X+2]=M[X]+2=n*p+2=4
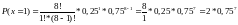 .
Стоит заметить, что
.
Стоит заметить, что
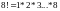 ,
а
,
а
 ,
поэтому мы можем сократить 8! и 7!, получив
в остатке 8. Таким образом, часто удается
сократить n!
и (n-m)!
либо m!.
,
поэтому мы можем сократить 8! и 7!, получив
в остатке 8. Таким образом, часто удается
сократить n!
и (n-m)!
либо m!.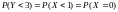
 .
Стоит заметить, что Х не может быть
меньше 0 или больше 8, т.к. Х – число
выигрышей.
.
Стоит заметить, что Х не может быть
меньше 0 или больше 8, т.к. Х – число
выигрышей.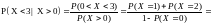
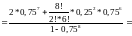

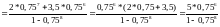 .
.
Стоит
отметить, что в данном случае
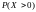 рациональнее было расписать как
рациональнее было расписать как
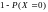 ,
а не P(X=1)+P(X=2)+….
,
а не P(X=1)+P(X=2)+….
Теперь решим текстовую задачу:
Вероятность изготовления нестандартной детали равна 0.11. Пользуясь формулой Бернулли найти вероятность того, что из пяти наудачу взятых деталей будут четыре стандартных.
Решение:
Итак,
нам дано: q=0,11,
n=5,
m=4.
Отсюда находим
 .
.
Теперь
используя формулу Бернулли, найдем
искомую вероятность:
 .
Ответ: 0, 345.
.
Ответ: 0, 345.
