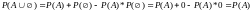- •Карточка. Тервер.
- •2 Курс.
- •Оглавление.
- •Глава I. Основные определения и обозначения.
- •Базовые обозначения
- •Пересечение. Объединение. Независимость.
- •Глава II. Характеристики случайной величины.
- •Глава III. Распределения
- •3.1 Равномерное распределение
- •3.2Дискретное распределение. Таблица.
- •1.3Нормальное распределение.
- •1.4Биномиальное распределение.
- •1.5 Экспоненциальное (показательное) распределение.
- •1.6 Пуассоновское распределение.
- •Глава IV. Формулы полного распределения и Байеса
Карточка. Тервер.
2 Курс.
Правила пользования:
Не разбирать и не давать детям.
Не передавать иным лицам без разрешения автора.
Прежде, чем заявлять, что здесь есть ошибка – проверьте.
Оглавление.
Глава I. Основные определения и обозначения……………………………………………3
Базовые обозначения………………………………………………………………………..…3
Пересечение. Объединение. Независимость……………………………………………..….4
Глава II. Характеристики случайной величины…………………………………………..6
Глава III. Распределения………………………………………………………………………9
3.1 Равномерное распределение……………………………………………………………....9
3.2 Дискретное распределение………………………………………………………………..9
3.3Нормальное распределение………………………………………………………………10
3.4 Биномиальное распределение…………………………………………………...………12
3.5 Показательное распределение……………………………………………………...……13
3.6 Пуассоновское распределение…………………………………………………...………14
Глава IV. Формулы полного распределения и Байес……………………………………16
Глава I. Основные определения и обозначения.
Базовые обозначения
 пространство
элементарных событий, множество всех
возможных событий.
пространство
элементарных событий, множество всех
возможных событий.
A, B, C и т.д. – события.
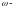 элементарный
исход.
элементарный
исход.
 -
пустое множество.
-
пустое множество.
P(A)
– вероятность того, что событие
произойдет. Представляет собой отношение
количества благоприятных исходов к
количеству всех исходов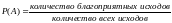 .
При
этом:
.
При
этом:
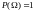 ,
а
,
а
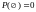 .
.
Пример:
представим себе подбрасывание монеты.
Сам процесс подбрасывания – случайный
эксперимент.
Выпадение орла – элементарный
исход
(как и выпадение решка). Событием,
в данном случае, будет выпадение орла,
выпадение 2-х решка подряд и т.д. Событие
отличается от элементарного исхода
тем, что оно шире, т.е. элементарный исход
– самое простое событие, которое может
произойти. Совокупность же элементарных
исходов составляет пространство
элементарных событий.
В нашем случае пространство элементарных
событий – выпадение решка и выпадение
орла. Вероятностью
выпадения
решка равняется:
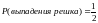 ,
т.к. кол-во благоприятных исходов – 1
(выпадение решка), кол-во всех исходов
– 2 (выпадение решка и выпадение орла).
,
т.к. кол-во благоприятных исходов – 1
(выпадение решка), кол-во всех исходов
– 2 (выпадение решка и выпадение орла).
Теперь оформим как задачу:
Дано:
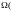 выпадение
решки; выпадение орла)
выпадение
решки; выпадение орла)
А – выпадение орла
P(A) - ?
Решение:
= .
.
Пересечение. Объединение. Независимость.
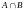 -
пересечение множеств, означает, что
элемент должен принадлежать одновременно
и
множеству А, и
множеству В. Графически можно представить
так:
-
пересечение множеств, означает, что
элемент должен принадлежать одновременно
и
множеству А, и
множеству В. Графически можно представить
так:
 .
.
Пример: пусть множество А – множество всех четных чисел, а множество В – множество чисел, делящихся на 3. Тогда их пересечением будут числа, делящиеся и на 2, и на 3 (6, 12, 18 и т.д.).
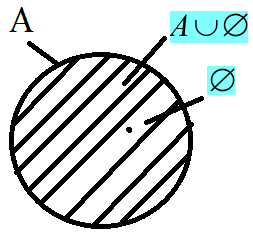
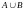 -
объединение множеств, означает, что
элемент должен принадлежать хотя
бы одному из множеств.
Графически можно представить так:
-
объединение множеств, означает, что
элемент должен принадлежать хотя
бы одному из множеств.
Графически можно представить так:
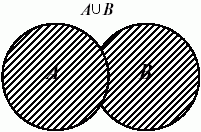
Пример: пусть множество А – множество всех четных чисел, а множество В – множество чисел, делящихся на 3. Тогда их пересечением будут числа, делящиеся на 2, или на 3, или одновременно на 2 и 3 (2, 3, 4, 6, 8, 9 и т.д.).
Основные формулы:
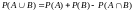
Если события А и В – независимы., то :
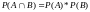
Если события А и В – зависимы, то:
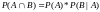 ,
где
,
где
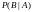 вероятность события В, при условии, что
событие А уже произошло.
вероятность события В, при условии, что
событие А уже произошло.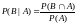
Критерий независимости событий:
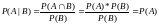
Теперь приведем самые распространенные частные случаи вероятностей и пересечений:
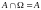 ,
но
,
но
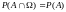 ,
действительно:
,
действительно:
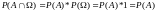 .
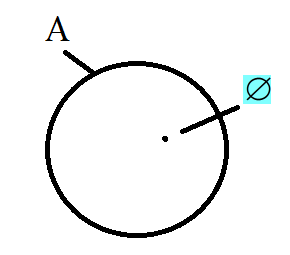
Графически это выглядит так:
.
Графически это выглядит так:
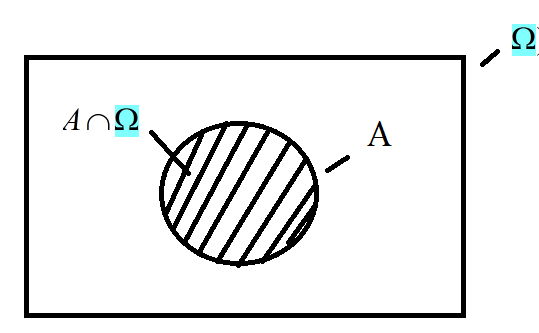
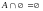 ,
но
,
но
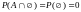 ,
действительно:
,
действительно:
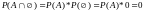
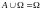 ,
но
,
но ,
действительно:
,
действительно:
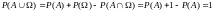
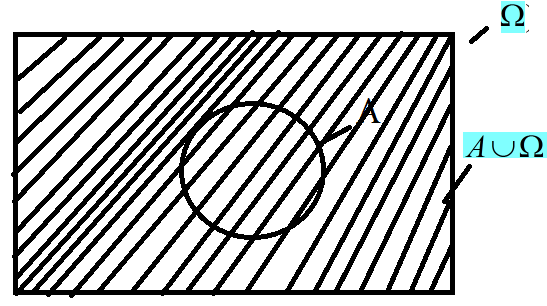
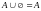 ,
но
,
но
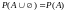 ,
действительно:
,
действительно: