Графічні зображення

Мета використання	► наочність
	► полегшення статистичного аналізу
	► ліпше засвоєння матеріалу, що вивчається

Вимоги	► правильний вибір зображення
	► назва
	► масштаб (рівень, явище, час)
	► умовні позначення

Види графічних зображень:

*діаграми: лінійні, секторні, радіальні, стовпчикові, внутрішньостовпчикові, об’ємні (куб, піраміда),фігурні (ліжка, люди)

*картограми

*картодіаграми

Об’ємна діаграма відображає статистичні величини у вигляді геометричних фігур (куб, куля, циліндр та ін.).

Фігурні діаграми – показники представлені у вигляді малюнків предметів, будинків лікарень, людей. Фігури тут відрізняються одна від одної величиною чи їх кількістю.

Картограма – це зображення статистичних величин на географічній карті, на якій окремі території заштриховані з різною інтенсивністю відповідно до рівня інтенсивного показника.

Картодіаграма – це зображення на географічній карті діаграм різного виду. Це дозволяє визначити коливання показників у регіонах.

Середні величини

Найбільш поширеною формою статистичних показників є середні величини, які дають узагальнену кількісну характеристику певної ознаки в статистичній сукупності за певних умов місця та часу. Середня величина одним числовим значенням характеризує всю масу певного явища.

В охороні здоров’я середні величини використовуються:

• для характеристики організації роботи закладів ОЗ (середня зайнятість ліжка, зайнятість ліжка в роботі, середня тривалість лікування хворого в стаціонарі та ін.);

• для характеристики показників фізичного розвитку (маса тіла, ріст, окружність голови, окружність грудної клітки та ін.);

• для визначення медико-фізіологічних показників організму (частота пульсу, частота дихання, артеріальний тиск та ін.);

• для оцінки даних медико-соціальних та санітарно-гігієнічних досліджень (середні норми харчового раціону, рівень радіаційного забруднення та ін.).

В медичній статистиці використовуються:

1. Середня арифметична (проста, зважена).

2. Мода (Mo) – це варіанта, яка має найбільшу частоту.

3. Медіана (Ме) – це варіанта, яка займає серединне (центральне) положення у варіаційному ряду.

Для визначення середньої величини необхідно використовувати результати індивідуальних вимірів, записуючи їх у вигляді варіаційного ряду. Варіаційний ряд – це ряд варіант(v) і відповідних їм частот(p). Варіантою (v) називають кожне цифрове значення ознаки, яка вивчається. Частота(p) – абсолютне число окремих варіант в сукупності, яка показує, скільки раз зустрічається дана варіанта у варіаційному ряду. Сума частот (p) дорівнює загальному числу спостережень – n.

Наприклад,

Результати виміру маси тіла у 25 юнаків віком 18 років (варіаційний ряд)

Маса тіла, кг (v) кількість осіб (p)

59. 1

60. 4

61. 6

62. 9

63. 3

64. 2

 (p) = n = 25

В нашому прикладі Мо = 62 кг, Ме = 62 кг. В даному випадку Мо = Ме.

Mmin – Mmax – це амплітуда ряду, тобто різниця крайніх значень ( 59 - 64).

Середня арифметична (M) – найбільш поширений за частотою використання вид середніх величин. Вона може бути простою і зваженою.

Середня арифметична проста – вираховується з варіаційного ряду, в якому кожна варіанта зустрічається тільки один раз; середня арифметична зважена вираховується з варіаційного ряду, в якому окремі варіанти зустрічаються кілька разів р  1.

Способи вирахування середньої величини

* проста M = v де: v – значення окремих варіант

n p – частота, з якою зустрічається

окрема варіанта;

* зважена n – загальне число одиниць

а) спосіб змішування M = vp спостережень

n

Середнє квадратичне відхилення () – це сумарне відхилення окремих варіант від середнього значення змінної (M) у вибірці.

Чим вищим є середнє квадратичне відхилення, тим вищим буде ступінь різноманітності ознак сукупності та менш типовою середня.

Способи вирахування :

* спосіб різниці  = Vmax – Vmin

К єрмолаєва

* простий спосіб  = +  d²

n d = v – M – це відхилення кожної варіанти від середньої

арифметичної

Якщо число спостережень рівне або менше 30 (n30), необхідно в знаменнику формул брати n-1.

Середнє квадратичне відхилення пов’язано зі структурою ряду розподілу ознаки. Схематично це можна зобразити наступним чином.

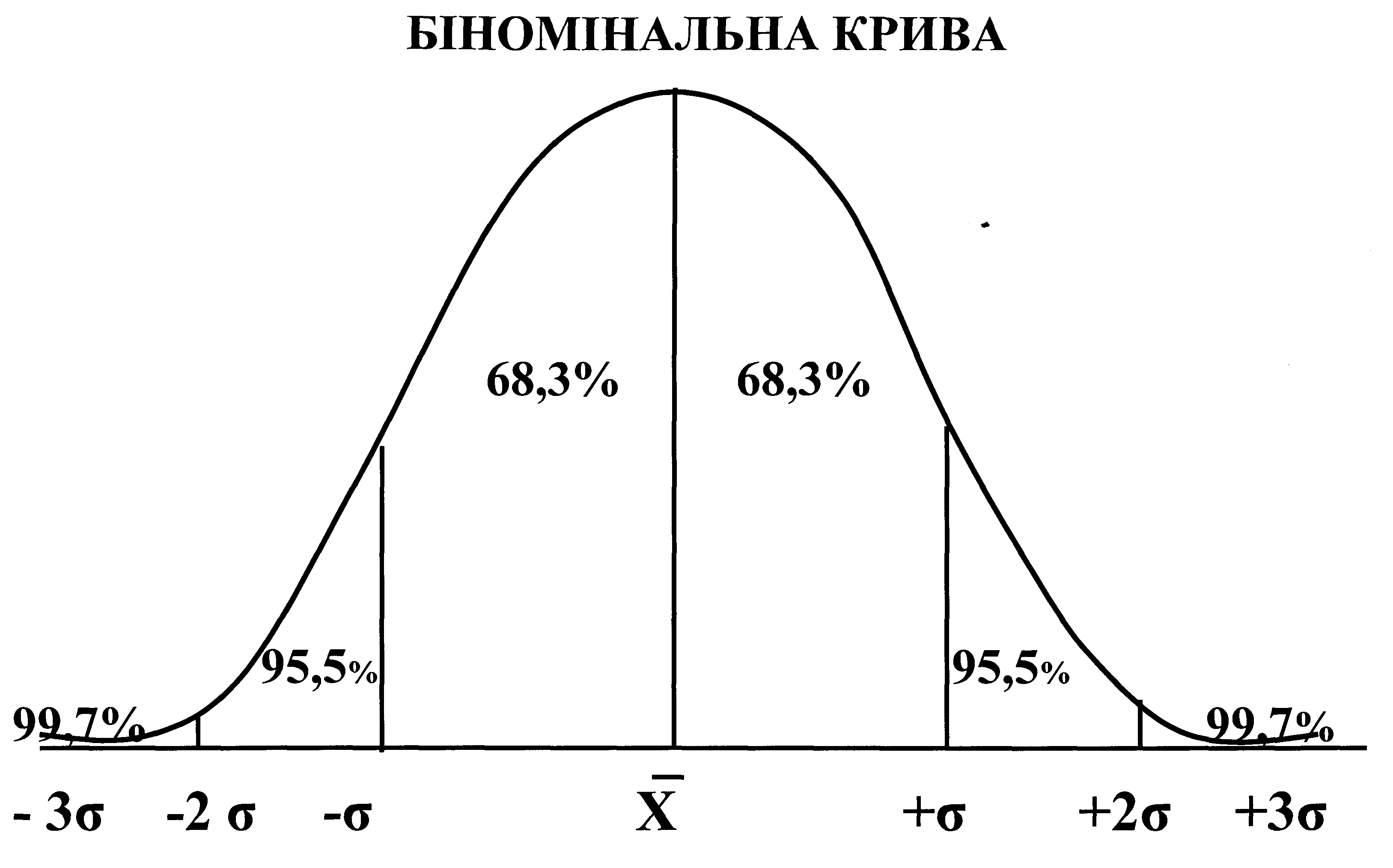
Теорією статистики доказано, що при нормальному розподілі (правило 3 –х ):

В межах M +  знаходиться 68,3% всіх варіант

M + 2 - 95,5% всіх варіант

M + 3 - 99,7% всіх варіант

Практично весь варіацйний ряд – 99,7% варіант знаходитиметься в діапазоні (M +  3). Окремі варіанти – до 0,3% можуть випадати з нього внаслідок занадто низького чи високого рівня (“вискакуючі”) варіанти.

Застосування правила 3 –х :

1. рішення питання щодо типовості середньої величини. Якщо 95% всіх варіант знаходияться в межах M + 2 то середня є характерною для даного ряду і не потребує збільшення кількості одиниць спостереження в сукупності;

2. знаючи M і  можна побудувати варіаційний ряд;

3. можна знайти амплітуду ряду.

Оцінити вірогідність результатів вибіркового дослідження означає визначити, в якій мірі зроблені для нього висновки (результати) можна перенести на генеральну сукупність.

Оцінка достовірності результатів передбачає визначення:

1. похибок репрезентативності (середніх похибок середньої арифметичної і відносних величин) – m;

2. довірчих меж середніх (або відносних) величин;

3. достовірність різниці середніх (або відносних) величин (за критерієм Стьюдента).

Оцінити достовірність результатів дослідження означає, встановити вірогідність безпомилкового прогнозу (р), з якою результати дослідження отримані на основі вивчення вибіркової сукупності, можна перенести на генеральну сукупність. Мірою достовірності середньої (відносної) величини являється середня помилка середньої арифметичної (m_х) або середня помилка відносної величини (m _% ).

Середня помилка (m) показує, на скільки результат, отриманий при вибірковому дослідженні, відрізняється від результату, який був би отриманий при суцільному дослідженні всієї генеральної сукупності.

Для визначення m _х використовують слідуючу формулу:

при n < 30 m _х = 

n – 1

при n > 30 m _х = 

n

Формула для визначення m _% :

при n < 30 m _% = P q

n – 1

при n > 30 m _% = P q,

n

де Р – величина показника, для якого визначається m _% , а q = 100 (1000) – Р.

За допомогою помилки можна визначити довірчі межі (максимально та мінімально можливі крайні значення) середньої (або відносної) величин. Довірчі межі – межі середніх (або відносних) величин, вихід за межі яких в результаті випадкових коливань має незначну вірогідність.

1. Для середньої величини: М = М + tm_x, де М – середня величина ознаки в генеральній сукупності, М – середня величина, яка отримана в результаті дослідження вибіркової сукупності, m_х - середня помилка, t – довірчий коефіцієнт – це величина, на яку потрібно помножити m для того, щоб з певною вірогідністю безпомилкового прогнозу (р) отримати межі коливання середньої величини в генеральній сукупності; tm – довірчий інтервал (або максимальна помилка).

2. Для відносних (альтернативних) величин: Р _% = Р _% + tm _%

П оняття “вірогідність безпомилкового прогнозу” (р) – це вірогідність, з якою можна стверджувати, що в генеральній сукупності М буде знаходитись в межах М + tm_x (або Р _% + tm _% ).

Якщо n < 30: при р = 95,5% критерій t знаходиться

при р = 99,7% за табл.Стьюдента

Я кщо n 30: при р = 95,5% t = 2

при р = 99,7% t = 3

ПРАВИЛО 3m

М = М + m – 68, 3%

М = М + 2m – 95,5%

М = М + 3m – 99,7%

Інтерпретація результату: в генеральній сукупності середня (відносна) величина з достовірністю 95,5% буде знаходитися в межах (....), а з достовірністю 99,7% в межах (....).

Розміри помилки залежать від коефіцієнту t, який вибирає сам дослідник, виходячи із необхідності отримати результат з певним ступенем вірогідності. Для абсолютної більшості медичних досліджень ступінь вірогідності безпомилкового прогнозу (р) повинна бути не менше 95,5%.

Із зменшенням величини помилки звужуються довірчі межі середніх і відносних величин, отриманих при вибірковій сукупності, тобто результати дослідження уточнюються та наближуються до відповідних величин генеральної сукупності. Потроєна помилка (3m) не повинна перевищувати 5% розміру результату, який оцінюється.

В наукових дослідженнях, як і в практичній роботі лікарів, використовують різні методи профілактики, діагностики і лікування. В цих випадках іноді виникає необхідність проведення оцінки достовірності різниці результатів різних методів, тобто вирішити питання, який з методів є кращий. Тому необхідно довести чи різниця між ними є суттєвою чи вона є випадковою.

Достовірність різниці між двома середніми (М₁ і М₂) або між двома відносними величинами (Р₁ і Р₂) визначається за критерієм Стьюдента за допомогою слідуючих формул:

t =  М₁ – М₂  і t =  Р₁ – Р₂ 

m²₁ + m²₂ m²₁ + m²₂

Величина t повинна бути рівна або більша 2. Тільки в цьому випадку з вірогідністю безпомилкового прогнозу, рівною 95,5%, можна стверджувати, що існує статистично значима різниця між порівнюваними середніми або відносними (альтернативними) величинами.