
- •Содержание:
- •1.3 Определение нагрузок на плиту покрытия……………………………………4
- •1. Конструирование и расчет ограждающей конструкции
- •1.1 Исходные данные
- •1.2 Конструирование и расчёт основной несущей конструкции покрытия
- •1.4 Расчёт плиты покрытия
- •1.4.1 Расчётные характеристики фанеры
- •1.4.2 Расчётные характеристики древесины
- •1.4.3 Определение геометрических характеристик расчетного поперечного сечения.
- •1.5.1 Расчётные усилия в сечениях плиты: Расчётные усилия в сечениях плиты:
- •1.5.2 Проверка на прочность растянутой (нижней) обшивки:
- •2.1 Определение нагрузок, действующих на арку
- •3. Статический расчет арки
- •3.1. Комбинации нагружения и соответствующие им эпюры изгибающих моментов:
- •4. Конструктивный расчет стрельчатой арки
- •4.1 Расчет арки на прочность
- •5. Конструирование и расчет конькового узла
- •6. Мероприятия по обеспечению пространственной жёсткости и неизменяемости здания.
- •7. Мероприятия по обеспечению долговечности основных несущих и ограждающих конструкций.
- •Список использованных литературных источников
3. Статический расчет арки
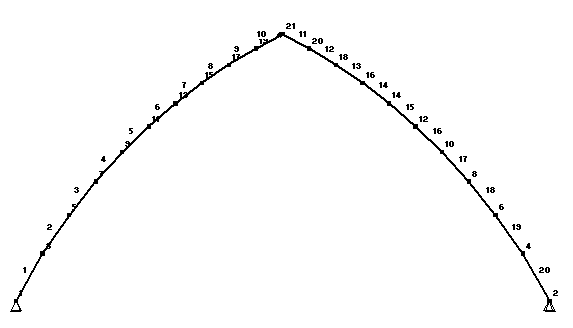
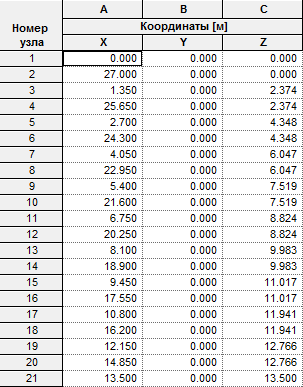
3.1. Комбинации нагружения и соответствующие им эпюры изгибающих моментов:
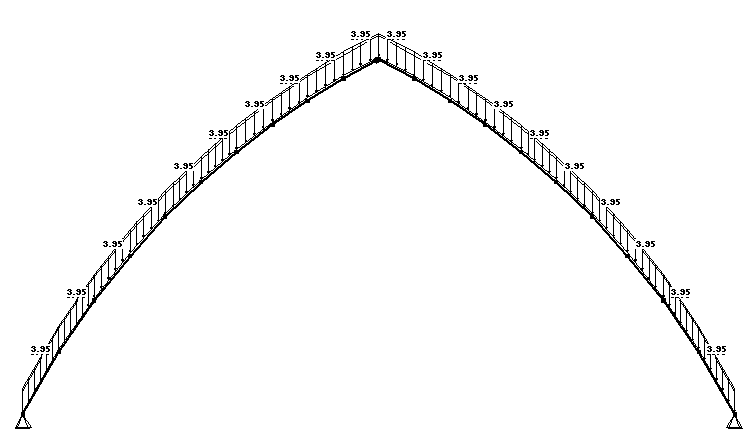
Рис. 3.1 Схема приложения нагрузки на арку от совместного действия постоянной и снеговой нагрузок
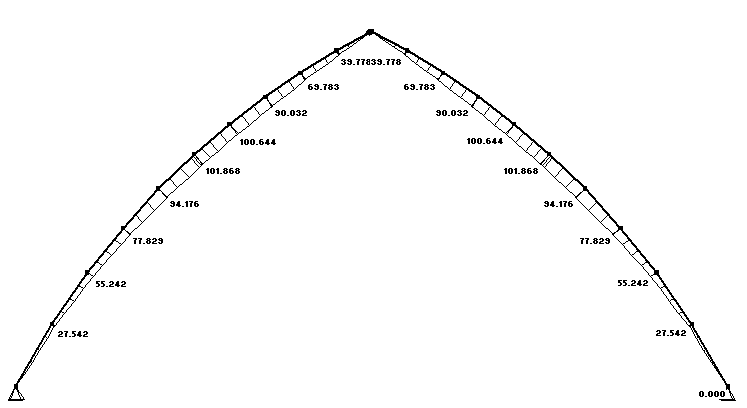
Рис. 3.2 Эпюра изгибающих моментов
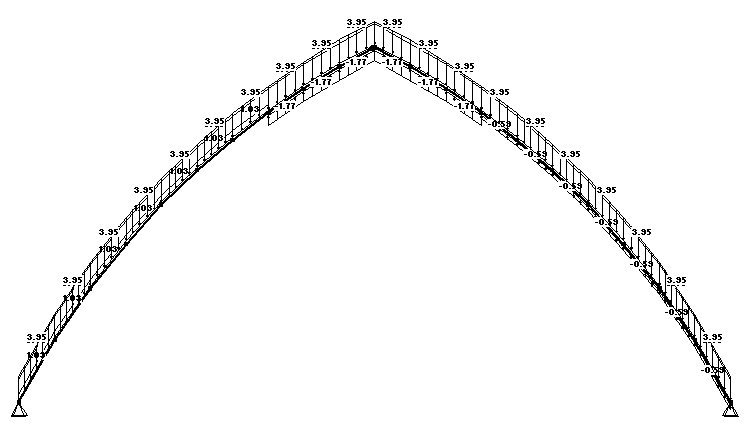
Рис. 3.3 Схема приложения нагрузки на арку от совместного действия постоянной, снеговой и ветровой (с понижающим коэффициентом 0,9) нагрузок
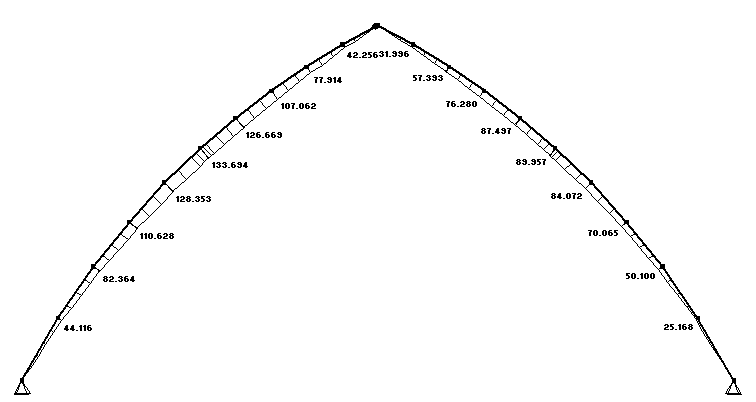
Рис. 3.4 Эпюра изгибающих моментов
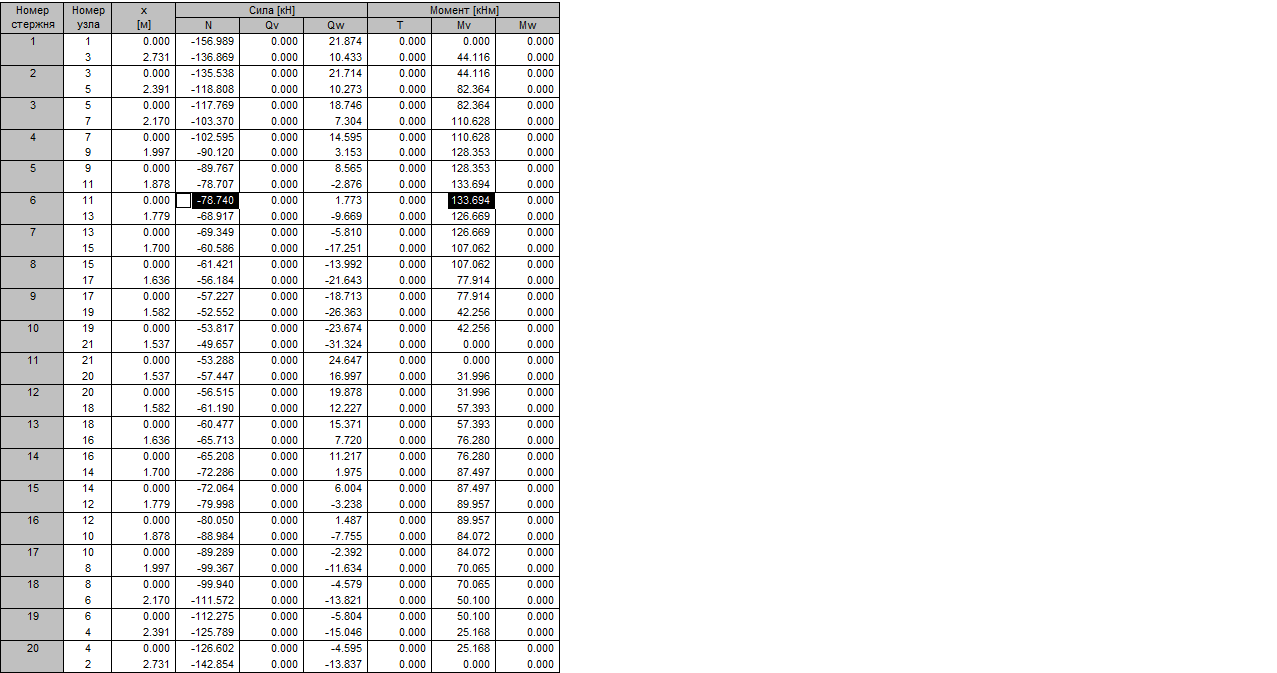
Наибольший момент при данном нагружении M(max)=133,694кНм,
соответствующее ему сжимающее усилие составит N=78,74 кН.
4. Конструктивный расчет стрельчатой арки
Для изготовления арок принимаем пиломатериал из древесины лиственница, кроме европейской и японской, II сорта 40х275мм.
Оптимальная высота сечения арки находится в пределах:
h=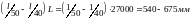 .
.
Принимаем поперечное
сечение арки 265561
мм из 17 слоев толщиной 33мм -

Согласно [2] расчетное сопротивление сжатию и изгибу fm.d= fc.o.d=15МПа табл. 6.4 [2].
Коэффициент условий
работы kmod=
1,05 (табл. 6.3
[2]); при h=561мм
kh=0,98
(табл. 6.8 [2]); при =33
мм k
= 1 (табл. 2.8 [1]); при
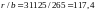 kr
= 0,8 (табл. 6.10
[2]); kx
= 1,2; kt=1;
ks=0,9.
kr
= 0,8 (табл. 6.10
[2]); kx
= 1,2; kt=1;
ks=0,9.
С
учетом коэффициентов расчетные
сопротивления сжатию и изгибу равны
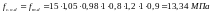
4.1 Расчет арки на прочность
выполняем в соответствии с п. 7.6.1[2] при изгибе с осевым сжатием должно удовлетворяться следующее условие 7.21[2]:
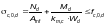
где
 —
изгибающий момент от действия поперечной
нагрузки;
—
изгибающий момент от действия поперечной
нагрузки;
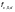 —
расчетное сопротивление древесины
сжатию;
—
расчетное сопротивление древесины
сжатию;
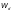 —
расчетный момент сопротивления
поперечного сечения;
—
расчетный момент сопротивления
поперечного сечения;
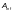 —
площадь расчетного сечения нетто;
—
площадь расчетного сечения нетто;
 — коэффициент,
учитывающий дополнительный момент от
продольной силы вследствие прогиба
элемента.
— коэффициент,
учитывающий дополнительный момент от
продольной силы вследствие прогиба
элемента.
Согласно п.7.6.2:
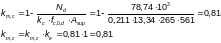
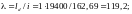
где
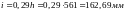 -
радиус инерции сечения;
-
радиус инерции сечения;
Полученная гибкость
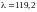 не превышает предельную
не превышает предельную
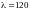 (таблица
7.7[2]).
(таблица
7.7[2]).
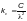 при
при
 по формуле 7.7[2]– коэффициент
продольного изгиба;
по формуле 7.7[2]– коэффициент
продольного изгиба;
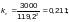
В
случае, когда эпюра изгибающих моментов
не соответствует очертанию, указанному
в 7.6.2[2], коэффициент
следует
умножать на поправочный
коэффициент 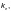 определяемый
по формуле
определяемый
по формуле
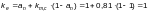
где 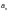 —
коэффициент, учитывающий очертание
эпюры изгибающих моментов, определяется
по таблице 7.6[2].
—
коэффициент, учитывающий очертание
эпюры изгибающих моментов, определяется
по таблице 7.6[2].
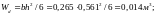
Тогда подставляя все найденные значения в формулу 7.21[2] получим:

Условие прочности
выполняется, следовательно, запроектированная
конструкция арки с сечением
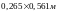 удовлетворяет требованиям прочности.
удовлетворяет требованиям прочности.
4.2. РАСЧЕТ АРОК НА УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ДЕФОРМИРОВАНИЯ
производим по формуле 7.24 [2]. Покрытие из плит шириной 1,55 м раскрепляет верхнюю кромку арки, для этого устраиваем раскосы через 2 плиты, lm=3,1м.
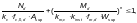 ,
,
где
 —
площадь брутто с максимальными размерами
сечения элемента на участке lm;
—
площадь брутто с максимальными размерами
сечения элемента на участке lm;
Wsup — максимальный момент сопротивления брутто на участке lm;
n = 2 — для элементов без закрепления растянутой зоны из плоскости деформирования на участке lm и n = 1 — для элементов, имеющих такие закрепления;
kс — коэффициент продольного изгиба, определяемый по формуле (7.7)[2] для любой гибкости участка элемента расчетной длиной lm из плоскости деформирования;
km,c — коэффициент, определяемый по формуле (7.22)[2];
kinst — коэффициент, определяемый по формуле (7.19)[2].
где - радиус инерции сечения;
Полученная гибкость не превышает предельную (таблица 7.7[2]).
при по формуле 7.7[2]– коэффициент продольного изгиба;
Согласно п.7.6.2:
В случае, когда эпюра изгибающих моментов не соответствует очертанию, указанному в 7.6.2[2], коэффициент следует умножать на поправочный коэффициент определяемый по формуле
где — коэффициент, учитывающий очертание эпюры изгибающих моментов, определяется по таблице 7.6[2].
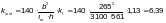
где
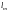 —
расстояние между точками закрепления
сжатой кромки от смещения из плоскости
изгиба;
—
расстояние между точками закрепления
сжатой кромки от смещения из плоскости
изгиба;
b — ширина поперечного сечения;
h — максимальная высота поперечного сечения на участке lm;
kf — коэффициент, зависящий от формы эпюры изгибающих моментов на участке lm, определяемый по таблице 7.4[2].
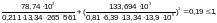
Следовательно, устойчивость обеспечена.
