4. Методика расчета сдвижений и деформаций земной поверхности

Для расчета сдвижений и деформаций земной поверхности при разработке угольных месторождений в нашей стране используется метод типовых кривых – безразмерных функций распределения основных видов сдвижений и деформаций, представляющих собой выраженные в безразмерной форме средние значения оседаний, наклонов, кривизны, горизонтальных сдвижений и деформаций. Типовые кривые, а также исходные данные, характеризующие особенности геологического строения, получены на основе статистической обработки результатов инструментальных наблюдений за сдвижением земной поверхности в основных угольных бассейнах и месторождениях.

В зависимости от полноты исходных данных находят ожидаемые или вероятные сдвижения и деформации. Ожидаемые сдвижения и деформации определяют в условиях, когда имеются календарные планы развития горных работ и известны необходимые для расчетов исходные данные. Вероятные сдвижения и деформации определяют, когда календарные планы горных работ отсутствуют.

Ожидаемые и вероятные сдвижения и деформации рассчитывают с определенной погрешностью, вызванной многими факторами, в том числе сглаживанием кривых сдвижения и деформаций, поэтому при решении задач подработки или строительства используются расчетные деформации.

Расчетные деформации получают путем умножения ожидаемых или вероятных сдвижений и деформаций на коэффициенты перегрузки: n_, n_, n_i, n_k, n_.

Исходными параметрами являются:

 граничные углы;

 угол максимального оседания и углы полных сдвижений;

 относительные максимальные оседания и горизонтальные сдвижения.

Рассмотрим расчет ожидаемых сдвижений и деформаций при отсутствии сдвижения пород лежачего бока. На разрезе вкрест простирания и по простиранию по граничным углам ₀, ₀, ₀ и углу максимального оседания  (при неполной подработке) или по углам полных сдвижений ₁, ₂, ₃ (при полной подработке) определяют длину полумульд L₁, L₂, L₃ (рис.28).

Максимальное оседание земной поверхности

_m = q₀mcosN₁N₂, (4.1)

где q₀ – относительное максимальное оседание, q₀ = ₀/m; ₀ – максимальное оседание при полной подработке; m – вынимаемая мощность пласта; N₁, N₂ – коэффициенты, учитывающие степень подработанности толщи соответственно вкрест и по простиранию пласта, определяется по Правилам охраны;  – угол падения пласта.

При применении закладки выработанного пространства вместо вынимаемой мощности пласта используют так называемую эффективную мощность пласта m_э. В большинстве случаев

m_э = h_к + h_н + [m – (h_к + h_н)]B₁, (4.2)

где h_к – сближение кровли и почвы (конвергенция) до возведения закладочного массива (рис.29), при отсутствии данных принимается равным 0,15m; h_н – неполнота закладки (среднее расстояние от верха закладочного массива до кровли на рис.29); В₁ – коэффициент усадки закладки (отношение изменения мощности закладочного массива под нагрузкой к его первоначальной мощности в неуплотненном состоянии) определяется из опыта или по компрессионным испытаниям закладочного материала, а при отсутствии данных – по таблице в Правилах охраны.

Если при расчетах коэффициентов получают значения N₁ > 1 или N₂ > 1, то принимают N₁ = N₂ = 1.

Различают максимальные оседания при полной подработке земной поверхности ₀ (когда N₁ = N₂ = 1) и при неполной подработке _m (при N₁ < 1 и N₂ < 1).

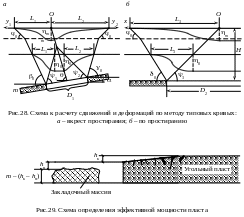
Начало координат находится в точке максимального оседания, ось x направлена по простиранию, ось y – в сторону падения y₁ и в сторону восстания y₂ (см. рис.28).

Оседания земной поверхности в точках главных сечений мульды сдвижения определяются по следующим формулам:

а) в полумульде по простиранию и в сторону, обратную простиранию,

_x,y = _mS(z_x); (4.3)

б) в полумульде по падению вкрест простирания пласта

; (4.4)

в) в полумульде по восстанию вкрест простирания пласта

, (4.5)

где S(z) – функция типовой кривой распределения оседаний, определяемая по таблицам Правил для соответствующих бассейнов (месторождений) в зависимости от коэффициентов N₁ – для точек главного сечения вкрест простирания пластов и N₂ – для точек главного сечения по простиранию пластов; z_x = x / L₃; z_y1 = y₁ / L₁; z_y2 = y₂ / L₂; x, y₁ и y₂ – расстояния от точки максимального оседания (начала координат) до рассматриваемой точки.

Наклоны в главных сечениях мульды:

а) по простиранию

; (4.6)

б) в сторону, обратную простиранию,

; (4.7)

в) в полумульде по падению

; (4.8)

г) в полумульде по восстанию

, (4.9)

где – значения функции типовой кривой наклонов, определяются по таблицам Правил для соответствующих бассейнов (месторождений), в зависимости от коэффициентов N₁ и N₂  z_x; z_y1; z_y2 – то же, что в формулах (4.3)- (4.5).

Кривизна в главных сечениях мульды при   45 определяется по формулам:

а) по простиранию

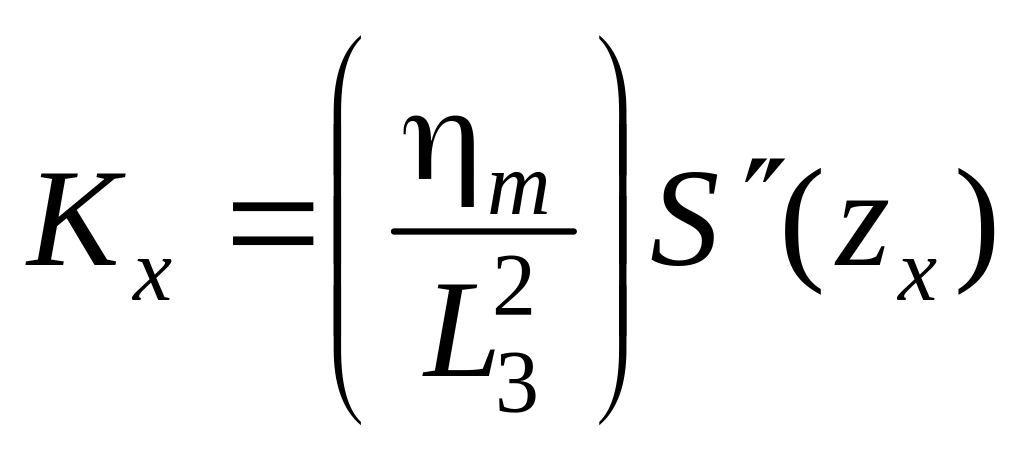; (4.10)

б) в полумульде по падению

; (4.11)

в) в полумульде по восстанию

, (4.12)

где – функция типовой кривой кривизны, определяемая по таблицам Правил для соответствующих бассейнов (месторождений), в зависимости от коэффициентов N₁ и N₂.

При неполной подработке (N_1,2  1) кривизна в точке максимального оседания определяется по средней длине полумульды L_ср = 0,5(L₁ + L₂).

Горизонтальные сдвижения в точках главных сечений мульды:

а) по простиранию

; (4.13)

б) в сторону, обратную простиранию,

; (4.14)

в) в полумульде по падению

; (4.15)

г) в полумульде по восстанию

, (4.16)

где значения функции определяются по таблицам Правил для соответствующих бассейнов (месторождений) в зависимости от коэффициента N₂; значения функций –по тем же таблицам Правил, в зависимости от коэффициента N₁.

Коэффициент В в формулах (4.15) и (4.16) определяется из выражения

, (4.17)

где  – угол падения пласта; h – мощность наносов; h_м – мощность горизонтально залегающих ( 5) мезозойских отложений; H_cр – средняя глубина разработки; а₀ – относительное максимальное горизонтальное сдвижение: отношение максимального горизонтального сдвижения _m к максимальному оседанию при полной подработке ₀, горизонтальном залегании пласта и закончившемся процессе сдвижения.

Проанализируем формулу (4.17):

1. При угле падения  = 0 и В < 0 (отрицательное значение) принимается В = 0, поскольку должно быть В  0. Значит, на разрезе по простиранию, где  = 0, типовые функции выбираются по таблицам Правил при В = 0, т.е. угол падения не учитывается. При отсутствии наносов и мезозойских отложений (h = 0 и h_м = 0) коэффициент В = (tg)/a₀.

2. Угол падения не оказывает влияния на горизонтальные сдвижения  и горизонтальные деформации , поэтому функции типовых кривых для вычисления наклонов и кривизны берутся при В = 0.

Горизонтальные деформации в точках главных сечений мульды:

а) по простиранию

; (4.18)

б) в полумульде по восстанию

; (4.19)

в) в полумульде по падению

. (4.20)

Значения функции определяются аналогично .

При неполной подработке (N < 1) горизонтальные деформации в точке максимального оседания определяются по средней длине полумульды L_cp = L₁ + 0,5L₂.

Расчеты сдвижений и деформаций от нескольких выработок в одном пласте или свите выполняются последовательно от каждой выработки; суммарные сдвижения и деформации от нескольких выработок определяются путем алгебраического сложения сдвижений и деформаций от каждой выработки.

При расчетах сдвижений и деформаций от нескольких выработок учитывается активизация процесса сдвижения, возникающая за счет трещин расслоений и отслоений, образовавшихся от первичной подработки. Под активизацией процесса сдвижения понимают изменение характера распределения и размера сдвижений и деформаций горных пород при повторных подработках смежными выработками или свитой пластов по сравнению со сдвижениями и деформациями от отдельной выработки при первичной подработке. Активизация процесса сдвижения увеличивает сдвижения и деформации земной поверхности, выполаживает углы сдвижения, граничные углы (т.е. увеличивается зона сдвижения). Активизация учитывается через изменение значения относительного максимального оседания q₀.