Вопрос 19. Теорема об изменении главного момента количеств движения системы (теорема моментов).

Теорема моментов для одной материальной точки будет справедлива для каждой из точек системы. Следовательно, если рассмотреть точку системы с массой  , имеющую скорость  , то для нее будет

где  и   - равнодействующие всех внешних и внутренних сил, действующих на данную точку.

Составляя такие уравнения для всех точек системы и складывая их почленно, получим:

Но последняя сумма по свойству внутренних сил системы равна нулю. Тогда найдем окончательно:

Полученное уравнение выражает следующую теорему моментов для системы: производная по времени от главного момента количеств движения системы относительно некоторого неподвижного центра, равна сумме моментов всех внешних сил системы относительно того же центра.

Проектируя обе части равенства на неподвижные оси Охуz , получим:

         

Уравнения выражают теорему моментов относительно любой неподвижной оси.

В кинематике было показано, что движение твердого тела в общем случае сла­гается из поступательного движения вместе с некоторым полюсом и вращательного движения вокруг этого полюса. Если за полюс выбрать центр масс, то поступательная часть движения тела может быть изу­чена с помощью теоремы о движении центра масс, а вращатель­ная - с помощью теоремы моментов.

Практическая ценность теоремы моментов состоит еще в том, что она, аналогично теореме об изменении количества движения, по­зволяет при изучении вра­щательного движения системы исключать из рас­смотрения все наперед неиз­вестные внутренние силы.

№20 МОМЕНТ ИНЕРЦИИ - величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают M. и. осевые и центробежные. Осевым M. и. тела относительно оси z наз. величина, определяемая равенством

где m_i - массы точек тела, h_i - их расстояния от оси z, r - массовая плотность, V - объём тела. Величина I_z является мерой инертности тела при его вращении вокруг оси (см. Вращательное движение). Осевой M. и. можно также выразить через линейную величину r_z, наз. радиусом инерции относительно оси z, по ф-ле I_z = Mr²_z, где M - масса тела. Размерность M. и.- L²M; единицы измерения -кг^.м².

Центробежными M. и. относительно системы прямоуг. осей х, у, z, проведённых в точке О, наз. величины, определяемые равенствами

или соответствующими объёмными интегралами. Эти величины являются характеристиками динамич. неуравновешенности тела. Напр., при вращении тела вокруг оси z от значений I_xz и I_yz зависят силы давления на подшипники, в к-рых закреплена ось.

M. и. относительно параллельных осей z и z' связаны соотношением (теорема Гюйгенса)

где z' - ось, проходящая через центр массы тела, d - расстояние между осями.

M. и. относительно любой проходящей через начало координат О оси Ol с направляющими косинусами a, b, g находится по ф-ле

Зная шесть величин I_x, I_y, I_z, I_xy, I_yz, I_zx, можно последовательно, используя ф-лы (4) и (3), вычислить всю совокупность M. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно перпендикулярные оси, наз. гл. осями инерции, для к-рых I_xy = I_yz = I_zx = 0. Тогда M. и. тела относительно любой оси можно определить, зная гл. оси инерции и M. и. относительно этих осей.

M. и. тел сложной конфигурации обычно определяют экспериментально. Понятием о M. и. широко пользуются при решении мн. задач механики и техники. Лит.: Гернет M. M., Ратобыльский В. Ф., Определение моментов инерции, M., 1969; Фаворин M. В., Моменты инерции тел. Справочник, M., 1970; см. также лит. при ст. Динамика. С. M. Таре.

Момент инерции тела относительно оси. Радиус инер­ции.

Положение центра масс характеризует распределение масс системы не полностью. Например (рис.32), если расстояния h от оси Oz каждого из одинаковых шаров А и В увеличить на одну и ту же величину, то положение центра масс системы не изменится, а распределение масс станет другим, и это скажется на движении системы (вращение вокруг оси Oz при прочих равных условиях будет происходить медленнее).

Рис.32

 

Поэтому в механике вводится еще одна характеристика распре­деления масс - момент инерции. Моментом инерции тела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси

Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.

Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.

Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является ме­рой инертности тела при вра­щательном движении.

Согласно формуле момент инерции тела равен сумме момен­тов инерции всех его частей от­носительно той же оси. Для од­ной материальной точки, нахо­дящейся на расстоянии h от оси,  .

Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина  , определяемая равенством

,

где М - масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.

В случае сплошного те­ла, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве  , обратится в интеграл. В результате, учи­тывая, что  , где   - плотность, а V-объем, получим

 или 

Интеграл здесь распространяется на весь объем V тела, а плотность   и расстояние h зависят от координат точек тела.

Моменты  инерции некоторых однородных тел:

1.Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относи­тельно оси Аz, перпендикулярной к стержню и прохо­дящей через его конец А (рис. 33).

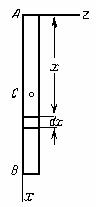
Рис.33

 

Направим вдоль АВ координатную ось Ах. Тогда для любого элементарного отрезка длины dx величина h=x, а масса  , где   - масса единицы длины стержня. В результате

Заменяя здесь   его значением, найдем окончательно:

2. Тонкое круглое однородное кольцо радиуса R и массы М. Найдем его момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр (рис.34,а). Так как все точки кольца находятся от оси Cz на расстоянии h_k=R, то

Следовательно, для кольца 

Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относитель­но ее оси.

3. Круглая однородная пластина или цилиндр ра­диуса R и массы М. Вычислим момент инерции круглой пла­стины относительно оси Сz, перпендикулярной к пластине и прохо­дящей через ее центр (см. рис.34,а). Для этого выделим элементарное кольцо радиуса r и ширины dr (рис.34,б).

               

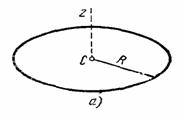
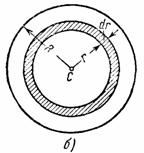
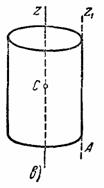
Рис.34

 

Площадь этого кольца равна  , а масса  , где  - масса единицы площади пластины. Тогда для выделенного элементарного кольца будет

а для всей пластины    . Заменяя здесь   его значением, найдем окончательно 

Такая же формула получится, очевидно, и для момента инерции   однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.34,в).

4. Прямоугольная пластина, конус, шар. Опуская выкладки, приведем формулы, определяющие моменты инерции следующих тел:

а) сплошная прямоугольная пластина массы М со сторонами АВ = а и BD = b (ось х направлена вдоль стороны AB, ось у - вдоль BD):

б) прямой сплошной круглый конус массы М с радиусом основания R (ось z направлена вдоль оси конуса):

г) сплошной шар массы М и радиуса R (ось z направлена вдоль диаметра): 

 

Моменты инерции тела относительно параллельных осей. Теорема Гюйгенса.

Моменты инерции данного тела относи­тельно разных осей будут, вообще говоря, разными. Покажем, как зная момент инерции относительно какой-нибудь одной оси, проведен­ной в теле, найти момент инерции от­носительно любой другой оси, ей па­раллельной.

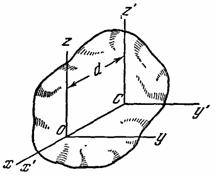
Р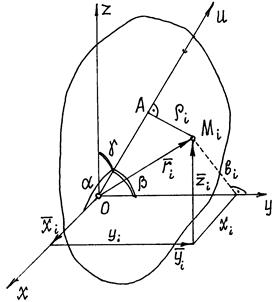 ис.35

 

Проведем через центр масс С тела произвольные оси Cx'y'z', а через лю­бую точку О на оси Сх' - оси Oxyz, такие, что ОyСy', OzCz' (рис. 35). Расстояние между осями Cz' и Оzобозначим через d. Тогда  

По определению момент инерции  .

Поместим в точку О начало координатных осей x, y, z. Из прямоугольного треугольника ОАМ_i следует  , где  . И так как радиус-вектор точки , то, проектируя это равенство на ось u, получим   ( ,  ,   - углы между осью u и осями x, y, z).

Рис. 14.3.

Как известно из тригономет­рии 

Поэтому

 

И, группируя подобные члены, содержащие косинусы одинаковых углов, получим:

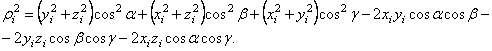
Но   - расстояния от точки М_i до осей x, y, z, соответственно. Поэтому

или         (2)

где I_x, I_y, I_z – моменты инерции тела относительно осей координат; I_xy, J_yz, J_xz  - центробежные моменты инерции относительно осей отмеченных в индексах.

Если два центробежных момента инерции, оба содержащих в индексах названия какой-нибудь одной оси, равны нулю, то эта ось называется главной осью инерции. Например, если J_yz = 0 и J_xz= 0, то ось z – главная ось инерции.

Так как все моменты инерции зависят от того, где находится точка О, от выбора начала координат, то обязательно надо указать для какой точки определены эти моменты инерции. Если начало координат взято в центре масс С, то все главные оси инерции называются главными центральными осями инерции.

Если в данной точке координатные оси являются главными осями инерции (центробежные моменты инерции относительно их равны нулю), то формула (2) упрощается:

.                           (3)

Иногда по некоторым признакам нетрудно найти главные оси инерции тела. . Если у однородного тела имеется ось симметрии, то эта ось является главной центральной осью инерции.

Действительно. Направим координатную ось z по оси симметрии. Тогда для каждой точки тела с координатами (x_i, y_i, z_i) можно отыскать точку с координатами (-x_i, -y_i, -z_i) и поэтому центробежные моменты инерции   и  . Значит ось z – главная ось инерции, и центральная ось, т.к. центр масс, как известно, находится на оси симметрии. Причём, эта ось будет главной для любой точки расположенной на оси симметрии.

2.  Если у однородного тела имеется плоскость симметрии, то любая ось перпендикулярная ей будет главной осью инерции для всех точек этой плоскости.

Направим ось z перпендикулярно плоскости симметрии из любой её точки О, назначив там начало координат. Тогда для каждой точки тела с координатами  (x_i, y_i, z_i) можно найти симметричную ей точку с координатами (x_i, y_i, - z_i). Поэтому центробежные моменты инерции I_xz и I_yz будут равны нулю. Значит ось z – главная ось инерции.

 

Пример 9. Определим момент инерции диска относительно оси u, расположенной под углом   к оси симметрии диска z (рис.37).

Рис.37

 

Оси x, y и z – главные центральные оси инерции, т.к. они являются осями симметрии.

Тогда  , где   - угол между осями u и z; угол   - угол между осями u и y, равный  ; угол   - угол между осями u и x, равный 90°. Поэтому

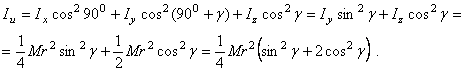
№21) Теорема об изменении главного момента количеств движения системы (теорема моментов).

Теорема моментов для одной материальной точки будет справедлива для каждой из точек системы. Следовательно, если рассмотреть точку системы с массой  , имеющую скорость  , то для нее будет

где  и   - равнодействующие всех внешних и внутренних сил, действующих на данную точку.

Составляя такие уравнения для всех точек системы и складывая их почленно, получим:

Но последняя сумма по свойству внутренних сил системы равна нулю. Тогда найдем окончательно:

Полученное уравнение выражает следующую теорему моментов для системы: производная по времени от главного момента количеств движения системы относительно некоторого неподвижного центра, равна сумме моментов всех внешних сил системы относительно того же центра.

Проектируя обе части равенства на неподвижные оси Охуz , получим:

         

Уравнения выражают теорему моментов относительно любой неподвижной оси.

В кинематике было показано, что движение твердого тела в общем случае сла­гается из поступательного движения вместе с некоторым полюсом и вращательного движения вокруг этого полюса. Если за полюс выбрать центр масс, то поступательная часть движения тела может быть изу­чена с помощью теоремы о движении центра масс, а вращатель­ная - с помощью теоремы моментов.

Практическая ценность теоремы моментов состоит еще в том, что она, аналогично теореме об изменении количества движения, по­зволяет при изучении вра­щательного движения системы исключать из рас­смотрения все наперед неиз­вестные внутренние силы.

2. Теорема о моментах инерции твёрдого тела относительно параллельных осей.

Момент инерции твердого тела относительно некоторой оси равен моменту инерции тела относительно параллельной оси проходящей через его центр масс, сложенному с произведением массы тела на квадрат расстояния между осями. Допустим, что задана ось Oz₁. Для доказательства теоремы проведём через центр масс тела С три взаимно перпендикулярные оси, из которых ось Сz параллельна заданной оси Oz₁, а ось Су лежит в плоскости параллельных осей Сz и Oz₁ (рис а, в). Обозначим d — расстояние между осями Cz и Oz₁. для вычисления моментов инерции тела относительно осей Cz и Oz₁ опустим из каждой точки M_i рассматриваемого тела перпендикуляры r_i и h_i на оси Cz и Oz₁. Выразим длины этих перпендикуляров через координаты этих точек:

r_i² = x_i² + y_i², h_i² = x_i² + (y_i — d)² = x_i² + y_i² + d² — 2y_id = r_i² + d² — 2y_id. (a)

Определим моменты инерции тела относительно осей Cz и Oz₁:

J_Cz = ∑ m_ir_i², J_z1 = ∑ m_ih_i².

Применив зависимость (а): J_z1 = ∑ m_ir_i² + ∑ m_id² — 2∑m_iy_id. (в)

Здесь ∑ m_i = m. — масса тела. Из формулы y_c = ∑ m_iy_i/m, получим:

∑ m_iy_i = my_c, так как y_c = 0, то ∑m_iy_i = 0. Подставляя это значение в равенство (в), получаем зависимость, установленную теоремой:

J_z1 = J_cz + md² . (г). Формула (г) показывает, что из совокупности паралельных осей ось, проходящая через центр масс тела, характеризуется наименьшим моментом инерции. Полярный момент тв. тела относительно центра масс: J_c = ½ * (J_cx + J_cy + J_cz). Отсюда следут, что ценр масс тела явл. полюсом, относительно которго полярный момент инерции тела имеет наименьшее возможное значение.

Воспользуемся формулой (г) для установления зависимости между радиусами инерции твёрдого тела i_cz  и i_z1относительно осей Cz и Oz_1.

J_z1 = mi_z1², J_cz = mi_cz², тогда mi_z1² = m_cz² + md², откуда i_z1² = i_cz² + d².

3. Теорема об изменении количества движения механической системы.

Изменение количества движения мех. сис. за некотрый промежуток времени равно геометрической сумме импульсов внешних сил приложенных к системе за тотже промежуток времени.

K = ∑ m_кυ_к; K = ∑ m_кdr_к/dt = d/dt * ∑m_кr_к = d/dt * mr_c = mdr_c/dt = mυ_c => K = mυ_c. Найдём призводную: dK/dt = d(mυ_c)/dt = mdυ_c/dt = ma_c Но из теоремы о движении ценра масс мех. сис. ma_c = R^E = ∑ P_к^E; dK/dt = ∑ P_к^E. Проинтегрируем это выражение: ∫_к1^к2dK = ∫_t1^t2∑P_к^Edt;

k₂-k₁=∑S_к^E — ч.т.д.