1 Вопрос Условия равновесия произвольной плоской системы сил

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы выполнялись условия (4.2.5):

Записывая условия равновесия в аналитической форме, можно привести три их классических вида:

1. Основная форма условий равновесия:

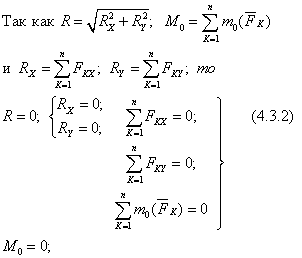
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций на оси координат были равны нулю и сумма моментов всех сил относительно центра О была равна нулю.

2. Вторая форма условий равновесия.

Для равновесия произвольной плоской системы необходимо и достаточно, чтобы сумма моментов относительно двух произвольно взятых точек тела была равна нулю и сумма проекций сил на одну из осей координат была равна нулю:

3. Уравнения трех моментов.

Дополнительное условие: А, В, С не лежат на одной прямой.

Вопрос 2. Момент силы относительно центра

Проекция силы на ось – это алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и вектором силы (т.е. это отрезок, откладываемый силой на соответствующие оси. Рисунок 1.13):

 F_x= Fcosα;

P_x= Pcosβ= P⋅ cos90^o=0;

R_x= Rcosγ = -R⋅ cos(180^o-γ).   

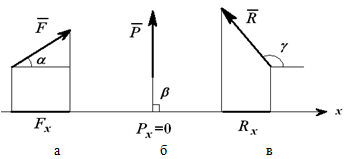
Рисунок 1.13

    Проекция силы на ось может быть положительной, рис. 1.13а (0 ≤ α < π/2), равной нулю, рис. 1.13б (β = π/2 ) и отрицательной, рис. 1.13в (π/2 < γ ≤ π).

    Иногда для нахождения проекции силы на ось сначала нужно найти ее проекцию на плоскость, а потом проекцию на ось (рисунок 1.14):

 P_z= P sinα;

P_x= (P cosα)cosβ;

Py= (P cosα)cosγ = P cosα⋅ cos(90^o-β).

Рисунок 1.14

Вопрос 3.Условия равновесия произвольной пространственной системы сил

Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор   и главный момент   были равны нулю, то есть система приводилась к случаю 5.2.1:

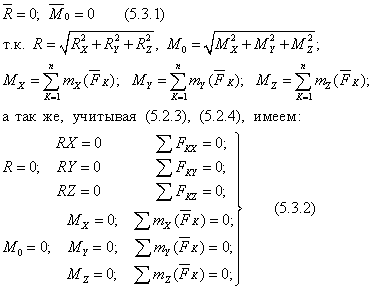
Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую ось и суммы их моментов относительно этих осей были равны нулю.

Для системы параллельных сил в пространстве необходимо и достаточно выполнение трех условий:

Вопрос 4. Момент силы относительно осей

Пусть данное тело вращается вокруг оси Oz и пусть сила   приложена в точке А. Проведем через точку А плоскость (ху) перпендикулярную Oz. Разложим силу   на две составляющие   и  . Составляющая  параллельна оси Оz и не может повернуть тело вокруг Oz. Таким образом, вращение дает составляющая  и

Для   принадлежащей плоскости Оxy и перпендикулярной оси Oz вращательный эффект равен произведению модуля силы на плечо h. Но этой же величиной измеряется момент силы относительно точки (центра) О.

Следовательно:

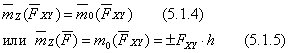
Моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.

Если с вершины оси Oz вращение тела видим против хода часовой стрелки, то момент берем со знаком плюс (+), иначе - знак минус (-).

Замечания:

1. Если сила параллельна оси, то ее момент равен нулю.

2. Если линия действия силы пересекает ось, то ее момент равен нулю.

3. Если сила перпендикулярна оси, то ее момент равен произведению модуля силы на расстояние до оси.

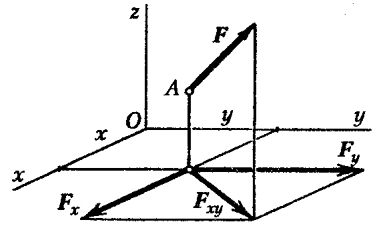
Для получения аналитического выражения моментов силы относительно осей координат, спроектируем силу   на плоскость Оху и разложим   на составляющие   и  . (рис. 32  )

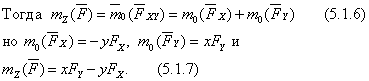
Аналогично можно записать для двух других осей.

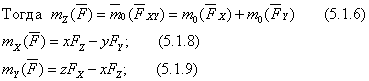
Рассмотрим каким же образом осуществляется зависимость между моментами силы относительно центра и относительно оси.

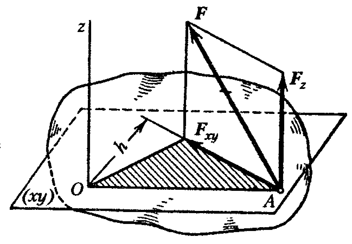
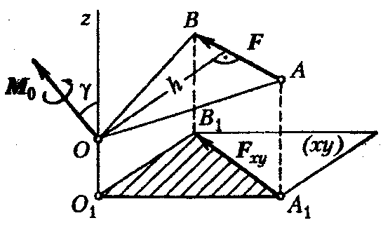
Пусть в точке А на тело действует сила   (рис. 33  ).

Моментом силы относительно произвольной точки О лежащей на оси Z, будет вектор   перпендикулярный плоскости ОАВ.

Проведем через   плоскость ху перпендикулярную  . Спроектируем   на плоскость  :

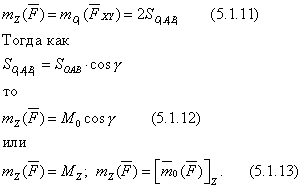
Момент силы   относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно любого центра, лежащего на оси.

31 рисунок 32 рисунок 33 рисунок