1. Понятия о форме и размерах земли; топографические план и карта. Масштабы планов и карт. Различие между планом и картой. Метод проекций.

• Топографической картой называется уменьшанное изображение значительной территории местности с искажениями

Топографический план – уменьшенное изображение незначительной территории, при котором искажения не влияют на точность измерений.

S меньше 20 км – план

S более 20 км – карта

Отличительные признаки  плана  и  карты: 

1) На планах изображается меньшая площадь,  нет  искажений  длин линий и углов. 

2) На планах не учитывается кривизна Земли. 

3) На  планах  используют  более  крупные масштабы: 1:500, 1:1000, 1:2000, 1:5000;

на картах - 1:10000, 1:25000, 1:50000, 1:100000.

4) На планах нет параллелей и меридианов, а имеется только координатная сетка.

5) Различается номенклатура,  т.е. система разграфки и обозначений отдельных листов карт и   планов.

Масштаб - отношение длины отрезков на планах или картах к горизонтальному проложению этого отрезка на местности.

Масштабы бывают: а) численный (в виде дроби), б) линейный (в виде линии), в) поперечный, позволяющий строить на чертежной бумаге с помощью измерителя и масштабной линейки отрезки с погрешностью равной 0,1 мм.

Под точностью масштаба понимают отрезок на местности соответствующий минимальному расстоянию на плане в 0,1 мм. Например, точность масштаба 1:500 соответствует 0.05м.

• R=6371 км

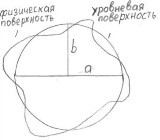
Фигура земли формируется под действием сил внутреннего тяготения и центробежной силы. Принято считать что земля имеет две поверхности: физическую образованную твердой оболочкой земли и уровневую поверхность мирового океана мысленно продолженную под сущей.

Тело ограниченное уровненной поверхностью называется геоидом. Геоид имеет сложную форму и не выражается математическим способом.

В связи с этим для математической обработки результатов геодезических измерений и  построений топокарт используют другую фигуру эллипсоид вращения.

Несмотря на то что поверхность геоида отклоняется или различается от поверхности эллипсоида на 105 м в практике инженерно геодезических работ принято считать одинаковыми.

Изоуровенную поверхность принимается средний многолетний уровень балтийского моря.

• Масштабом называется степень уменьшения горизонтальных проложений линий местности при изображении их на плане, карте или аэроснимке. Различают численный и графические масштабы; к последним относятся линейный, поперечный и переходный масштабы.

Численный масштаб. Численный масштаб выражается в виде дроби, числитель которой равен единице, а в знаменателе стоит число, показывающее степень уменьшения горизонтальных проложений. На топографических картах численный масштаб подписывается внизу листа карты в виде 1:М, например, 1:10000.

В нашей стране приняты следующие масштабы топографических карт: 1:1 000 000, 1:500 000, 1:200 000, 1:100 000, 1:50 000, 1:25 000, 1:10 000. Этот ряд масштабов называется стандартным. Раньше этот ряд включал масштабы 1:300 000, 1:5000 и 1:2000.

Линейный масштаб – это графический масштаб; он строится в соответствии с численным масштабом карты в следующем порядке:

• проводится прямая линия и на ней несколько раз подряд откладывается отрезок a постоянной длины, называемый основанием масштаба (при длине основания a=2 см линейный масштаб называется нормальным); для масштаба 1:10 000 a соответствует 200 м,

• у конца первого отрезка ставится нуль,

• влево от нуля подписывают одно основание масштаба и делят его на 20 частей,

• вправо от нуля подписывают несколько оснований,

• параллельно основной прямой проводят еще одну прямую и между ними прочерчивают короткие штрихи

Поперечный масштаб.

Порядок пользования поперечным масштабом:

• циркулем-измерителем зафиксировать длину линии на карте.

• одну ножку циркуля поставить на целое основание, а другую – на любую трансверсаль, при этом обе ножки циркуля должны располагаться на линии.

• д лина линии составляется из трех отсчетов: отсчет целых оснований, умноженный на цену основания, плюс отсчет делений левого основания, умноженный на цену деления левого основания, плюс отсчет делений вверх по трансверсали, умноженный на цену наименьшего деления масштаба. Точность измерения длины линий по поперечному масштабу оценивается половиной цены его наименьшего деления.

2. Рельеф местности. Метод горизонталей.

Рельефом называют совокупность различных по форме неровностей земной поверхности.

Существуют 6 форм горизонталей (рельефа)

• Гора

• Коловина

• Хребет

• Седловина

• Лощина

• Ровнина

Свойства горизонталей:

• Точки, лежащие на одной горизонтали имеют одинаковую высоту

• Осадки, выпавшие на поверхность земли, стекаются перпендикулярно горизонталям в сторону понижения

• Все горизонтали, замыкающиеся в пределах плана или карты, обозначают или холм или

котловину; они опознаются по Берг штрихам или по надписям.

• Горизонтали не могут пересекаться на плане. Редкое исключение из этого

правила будет лишь в том случае, когда горизонталями изображается нависший утес.

3. Система географических координат. Понятие о зоне и колоне. Зональная система прямоугольных координат.

Географическая система координат . Географи́ческие координа́ты определяют положение точки на земной поверхности.

Долгота - № меридиана (лямбде)

Широта - № паралели (фи)

Географические зоны – по 6 меридиан от 0

Географические колонны – по 6 меридиан от 180 (различаются на 30 ед.)

Зональная система прямоугольных координат.

Ось Х – верх

Ось У – по экватору

Зона — это участок земной поверхности, ограниченный двумя меридианами.

4. Трасса линейного инженерного сооружения. Закрепление трассы местности . Работа пикетажа. Круговые кривые. Элементы круговой кривой.

Трассой называется ось проектируемого сооружения линейного типа обозначенное на местности или нанесенное на карту, фотоплан или в виде цифровой модели местности.

Основными элементами трассы являются план – ее проекция на горизонтальную плоскость.

В плане трасса состоит из прямых участков разных направлений сопрягающихся между собой горизонтальными кривыми постоянного или переменного радиуса кривизны.

Главные точки трассы:

• Н.Т

• К.Т.

• В .У.

Пикетажные точки – через каждые 100 м.

При измерении длинны линии ведётся запись в пикетажный журнал.

Закрепление пикетных точек: на месте пикета забивается колышек (сторожок) длиной 30 см

Круговая кривая - Круговая кривая – это дуга окружности, вписанная в угол, образованный двумя смежными линиями трассы.

Элементы:

• Т – тангенс

• К – кривая

• Б – биссектриса

• Д - домер

5. Вычислить пикетажные значения главных точек кривой - значит узнать на каких пикетах и плюсовых точках они находятся.

С начала определяют пикетаж вершины угла поворота ВУ, а затем находят пикетажное значение начала, конца и середины кривой

Для контроля вторично вычисляют пикетажное значение конца кривой

КК = ВУ + Т - Д .

П ример (рис. 84): Определены: пикетаж ВУ ПК1+12.48 и основные элементы круговой кривой:

Найти пикетажные значения НКК, ККК, СКК. Расчет пикетажа главных точек кривой выполняется в следующей форме:

6. Ориентировать линию – значит определить ее направление относительно другого, принятого за начальное. Направление определяется величиной ориентирного угла, т. е. угла между начальным направлением и направлением линии. За начальное направление принимают: географический меридиан точки, осевой меридиан зоны и магнитный меридиан точки.

Ориентирными углами линии являются дирекционный угол, географический (истинный) азимут, магнитный азимут и три румба: дирекционный, географический и магнитный.

Дирекционным углом линии называют горизонтальный угол α, измеренный по ходу часовой стрелки от северного направления осевого меридиана до ориентируемой линии. Средний меридиан зоны называется осевым; долгота осевого меридиана подсчитывается по формуле

L₀ = 6°n – 3°,          (1.4)

где  n – номер зоны.

Дирекционный угол изменяется от 0° до 360°.

Г еографическим (истинным) азимутом линии называется горизонтальный угол А_и, измеренный по ходу часовой стрелки от северного направления географического меридиана точки до ориентируемой линии. Пределы изменения географического азимута – от 0° до 360°. Связь географического азимута и дирекционного угла одной и той же линии выражается формулой

где γ_г –  гауссово сближение меридианов.

Г ауссово сближение меридианов – это горизонтальный угол γ_г между истинным меридианом и осевым меридианом зоны в данной точке.

Восточное сближение меридианов считают положительным, западное – отрицательным

Магнитным азимутом линии местности в данной точке называют горизонтальный угол А_m, измеренный по ходу часовой стрелки от северного направления магнитного меридиана, проходящего через данную точку, до ориентируемой линии. 

М агнитный меридиан – это проекция оси свободно подвешенной магнитной стрелки на уровенную поверхность. Магнитный азимут изменяется от 0° до 360°. Магнитный азимут линии вычисляется по формуле 1.5

где δ – склонение магнитной стрелки, А_и – географический (истинный) азимут линии.

Склонение магнитной стрелки – это горизонтальный угол δ, на который магнитный меридиан отклоняется от истинного (географического) в данной точке. Восточное склонение магнитной стрелки считают положительным, западное – отрицательным.

Румбом линии местности в данной точке называют горизонтальный угол r, измеренный от ближайшего направления меридиана (северного или южного) до направления данной линии. Пределы изменения румба от 0° до 90°. Название румба зависит от названия меридиана: географический (истинный), дирекционный или магнитный.

Дирекционный румб r_α, географический (истинный) r_и  и магнитный румб  r_т линии вычисляются по формулам:

1. 7

Номер четверти определяется по значению азимута: в 1-й четверти азимут изменяется от 0° до 90°, во 2-й четверти от 90° до 180°, в 3-й четверти – от 180° до 270°, в 4-й четверти – от 270° до 360°. Полное написание румба включает его числовое значение и название четверти (1-я – СВ, 2-я – ЮВ, 3-я – ЮЗ, 4-я – СЗ), например r_т = ЮВ: 45°10'.

В практике геодезических работ часто приходится передавать дирекционный угол на последующую линию через угол поворота. Для этого по известному дирекционному углу предыдущей линии α_пред. и углу поворота (β_л – левый угол илиβ_п – правый угол) вычисляется дирекционный угол последующей линии по формулам

α_{послед.} = α_пред.+ β_л – 180°;        (1.8)

α_{послед.} = α_пред.– β_пр + 180°.       (1.9)