Характеристики случайных величин. Математическое ожидание. Дисперсия. I
Математическим
ожиданием
непрерывной случайной величины
называется число
 ,
,
дискретной случайной
величины
 .
.
Пусть дискретная
случайная величины
принимает значения x1,
x2,…,
тогда
 .
.
Для действительной случайная величины
математическое
ожидание называетсяk-м
моментом,
называетсяk-м
моментом, называетсяабсолютным моментом k-го
порядка,
называетсяабсолютным моментом k-го
порядка,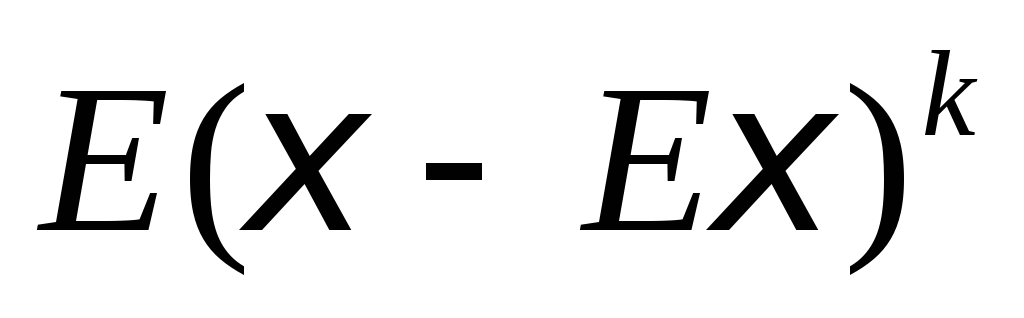 –центральным
моментомk-го
порядка,
–центральным
моментомk-го
порядка, –
абсолютнымцентральный моментомk-го порядка,
–
абсолютнымцентральный моментомk-го порядка, –факториальным
моментом k-го
порядка.Второй
центральный момент называется дисперсией
и обозначается
–факториальным
моментом k-го
порядка.Второй
центральный момент называется дисперсией
и обозначается
 =
= .
Корень квадратный из дисперсии называется
среднимквадратическим отклонением.
.
Корень квадратный из дисперсии называется
среднимквадратическим отклонением.
Смешанный центральный второй момент
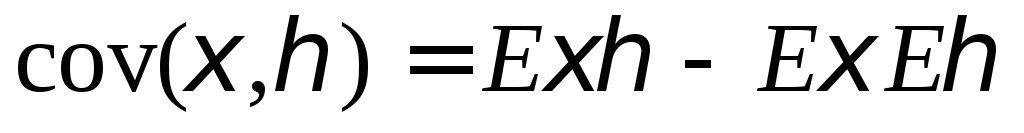 называется ковариацией случайных
величин ,
.
Коэффициентом корреляции ,
называется отношение
называется ковариацией случайных
величин ,
.
Коэффициентом корреляции ,
называется отношение
 .
.
Если =g()
, то для вычисления
 применяются формулы
применяются формулы
 ,
,
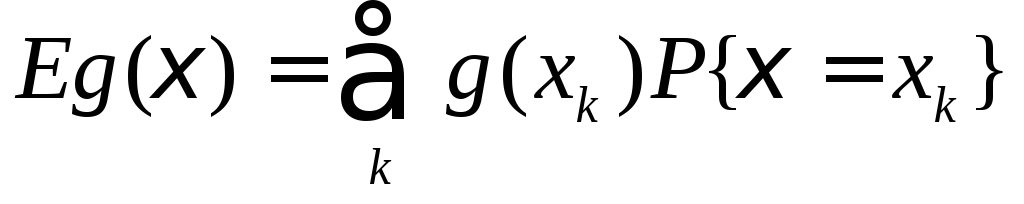 .
.
Для независимых
1,…,
n
справедливо равенство
 ,
,
 ,
kl,
,
kl,
в общем случае
 .
.
Свойства
математического ожидания и дисперсии:
1. для любых ,
с конечными E
и E
E(+)=E()+E();
2. для любого числа
c
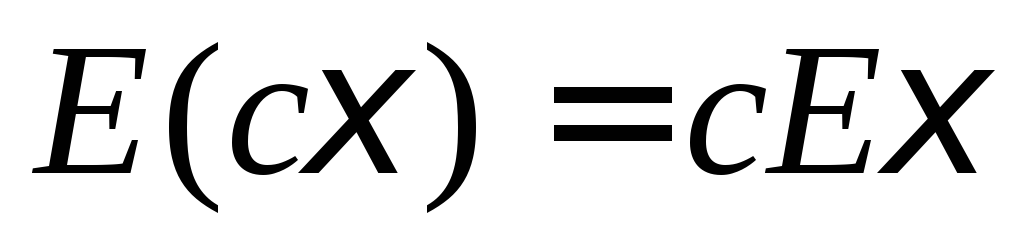 ;
;
 ;
;
 ;
;
 ;
;
3. для любых
независимых ,
с конечными E
и E
 .
.
Индикатором
события A
называется случайная величина A=A(),
принимающая значение 1, если A,
и 0, если A.
Часто оказывается, что можно указать
такие события A1,…,
An,
что интересующая нас величина
представляется в виде
 .
.
Это удобно тем,
что свойство аддитивности верно и для
зависимых слагаемых. Таким образом
 .
.

