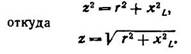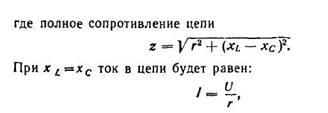1.Электрическая цепь и её элементы. Электрическая схема понятия-ветвь, узел, контур.

Электрической цепью называется совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электрическом токе, ЭДС (электродвижущая сила) и электрическом напряжении.

Электрическая цепь состоит из отдельных устройств или элементов, которые по их назначению можно разделить на 3 группы:

Первую группу составляют элементы, предназначенные для выработки электроэнергии (источники питания)

. Вторая группа — элементы, преобразующие электроэнергию в другие виды энергии (механическую, тепловую, световую, химическую и т. д.). Эти элементы называются приемниками электрической энергии (электроприемниками)

. В третью группу входят элементы, предназначенные для передачи электроэнергии от источника питания к электроприемнику (провода, устройства, обеспечивающие уровень и качество напряжения, и др.).

Цепи:

1.линейныетакие в состав которых входят лиейные элементы,которые не зависят от I и U

2.нелинейные те которые содержат не линейные элементы.

Электрическая схема-графическое изображение электрической цепи содержащее условные обозначения.

Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов

Узел электрической цепи (схемы) – место соединения трех и более ветвей.

Контур – любой замкнутый путь, проходящий по нескольким ветвям.

2.Источники ЭДС и источники тока, их эквивалентные схемы. внешнии характеристики

3.Работа и мощность в цепи постоянного тока.

Работа тока - это работа электрического поля по переносу электрических зарядов вдоль проводника; Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась.

Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока:

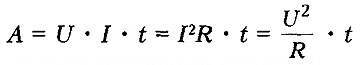
По закону сохранения энергии:

работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергия равна работе тока.

В системе СИ:

Мощность тока- отношение работы тока за время t к этому интервалу времени.

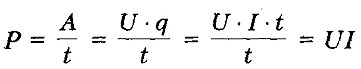В системе СИ:

P=I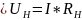

P=I*

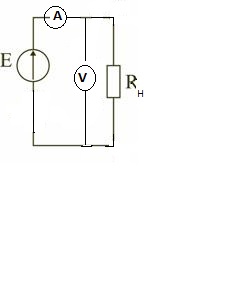
4.Закон Ома для полной цепи.

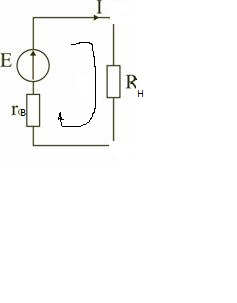сила тока замкнутой цепи прямо пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи.

Внутренним сопротивлением r_B ,током I электрической цепи и общим эквивалентным сопротивлением R_Н=r₀+R всей цепи:

.

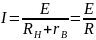Следствия:

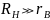,тоU=E(соответств. холостому ходу)

,тоI=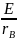 (соответств короткому замыканию)

5.Первый закон Киргофа.

Алгебраическая сумма токов в любом узле эл.цепи равна 0,при этом токи текущие к узлу и токи вытекающие из узла нужно брать с разными знаками.

,

где m – число ветвей подключенных к узлу.

6) 2-ой З. К.: алгебраическая сумма ЭДС в контуре равна, алгебраической сумме падений напряжений на сопротивление в контуре. (Сумма) Ек = (Сумма) Uк. 7)метод эквив. Генератора: применяется для расчета тока в какой то одной цепи а) разорвем ветвь в которой необходимо получить ток и получим эквив. Схему б) любым способом определяем U на участке разрыва в) определяем R эквив.  Г)сопротивления источника закорачиваем а внутреннее сопротивление оставляем 8)расчет цепей с помощью З. К. а) определяем число узлов и число независ. Контуров б) обозн на схеме токи в ветвях и произвольно выбираем их направление в) составляем(m-1) уравнение по 1-му З.К. г) составляем(n) уравнений по 2-му З. К. произвольно задаем направление обхода контура, при составлении уравнения ЭДС считается «+» если ее направление совпадает с направлением обхода 9) метод контурных токов а) произвольно задаем направление тока в цепях б) определяем кол-во независимых контуров и составляем уравнение по 2-му З. К. направление контурных токов выбираем произвольно, ЭДС со знаком «+» если совпадает с обходом контура. в) решаем систему находим ток(I) Ia, Ib, Ic. г) если какой либо ток отрицателен то его направление противоположно выбранному 10) метод узловых потенциалов а) обозначим цифрами или буквами все узловые точки схемы, потенциал одного узла примем равным 0. б) произвольно выбираем направление токов, но они текут от большего потенциала к меньшему, причем (фи1>фи2) в) составляем уравнение по 1-му З. К. г) решаем уравнение и определяем (фи1 и фи2) д)по потенциалам определяем токи в цепях е)любым способом проверяем правильность решения (более подробно можно посмотреть в тетради по практике!!!!!!!!)

16 Вопрос

Синусоидальный ток в емкости

Пусть напряжение на емкости С (рис.2.2,в) синусоидально:

)

тогда ток через емкость равен

где амплитуда тока 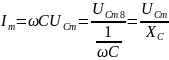, начальная фаза тока

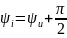
Величина X_C = 1/ωC, имеющая размерность сопротивления, называется

CL

емкостным сопротивлением, оно обратно пропорционально частоте f и является реактивным.

С увеличением частоты синусоидального напряжения и_С емкостное сопротивление X_C уменьшается. Это объясняется тем, что возрастает скорость изменения заряда dq / dt на пластинах емкостного элемента, а следовательно, увеличивается ток через него. Увеличение тока при

CL

неизменной амплитуде напряжения может быть связано только с уменьшением емкостного сопротивления X_C .

Сдвиг фаз между напряжением и током в емкости равен

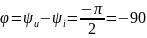(2.21)

следовательно, напряжение на емкости (рис.2.5) отстает от тока на 90⁰ (ток опережает напряжение на 90⁰). Физически это объясняется тем, что напряжение на емкости возникает за счет разделения зарядов на пластинах элемента в результате прохождения тока. Следовательно, напряжение и_С появляется только после возникновения тока. Из рис.2.5 видно, что нулевым значением тока соответствуют максимальные (положительные или отрицательные) значения напряжения. Это объясняется тем, что когда электрический заряд q и соответственно напряжение u_C=q/C достигают максимального значения, ток i равен нулю (du_C /dt = 0).

Амплитудные и действующие напряжения и токи в емкости связаны соотношением, подобным закону Ома:

17 Вопрос

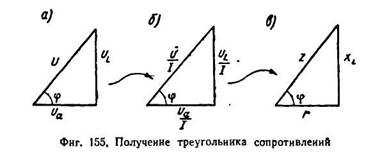
Треугольник сопротивлений

Если стороны треугольника напряжений (фиг. 155, а) разделить на ток I (фиг. 155, б), то углы треугольника от этого не из менятся, и мы получим новый треугольник, подобный первому — треугольник сопротивлений (фиг. 155, в).

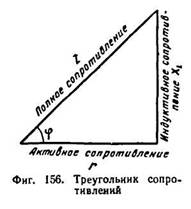
В треугольнике сопротивления, показанном отдельно на фиг. 156, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.

Из треугольника сопротивлений видно, что полное или кажущееся сопротивление z равно геометрической сумме активного r и индуктивного x_L сопротивлений.

Применяя теорему Пифагора к треугольнику сопротивлений, получаем:

Если одно из сопротивлений цепи - (активное или реактивное), например, в 10 и более раз меньше другого, то меньшим можно пренебречь, в чем легко убедиться непосредственным расчетом.

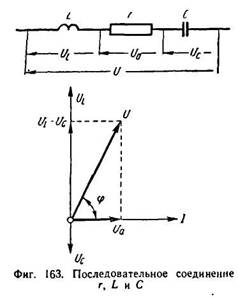
Последовательное соединение активного сопротивления, индуктивности и емкости (r, L, С)

На фиг. 163 даны схема и векторная диаграмма для цепи с последовательным соединением активного сопротивления, индуктивности н емкости. Напряжение на зажимах цепи равно сумме падений напряжения на отдельных участках цепи: активного падения напряжения н падений напряжений иа индуктивном и емкостном сопротивлениях.

Напряжения U_L и U_c сдвинуты между собой по фазе на полпериода (180°). Поэтому при геометрическом сложении векторов они взаимно вычитаются. Из векторной диаграммы находим:

 

т. е. цепь будет вести себя так, как будто она содержит только одно активное сопротивление. При этом ток и напряжение сети совпадают по фазе. Этот случай называется резонансом напряжений. График и векторная диаграмма для резонанса напряжений показаны на фиг. 164. Условием резонанса напряжений является равенство

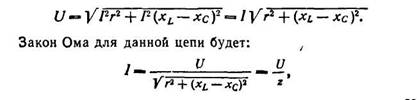
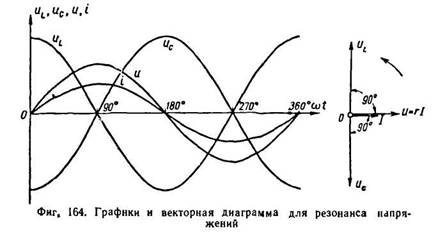
Поэтому резонанс напряжений может наступить: 1) если при постоянной индуктивности емкость меняется и становится равной:

 

2) если при постоянной емкости меняется индуктивность и становится равной:

3) если изменение обеих величин L и С приводит к равенству:

4) если, наконец, угловая частота сети, изменяясь, становится равной: