Ответы на экзаменационные вопросы по теории вероятности + Экзаменационные вопросы / Ответы на вопросы по теории вероятности прошлых лет / 34 Критерии согласия Колмогорова

34 Критерии согласия Колмогорова.

В статистике критерий согласия Колмогорова (также известный, как критерий согласия Колмогорова — Смирнова) используется для того, чтобы определить, подчиняются ли два эмпирических распределения одному закону, либо определить, подчиняется ли полученное распределение предполагаемой модели.

Критерий Колмогорова — Смирнова о проверке гипотезы об однородности двух эмпирических законов распределения является одним из основных и наиболее широко используемых непараметрических методов, так как достаточно чувствителен к различиям в исследуемых выборках.

Эмпирическая функция распределения (ЭФР) случайной величины , построенная по выборке , имеет вид:

где указывает, попало ли наблюдение X_i в область :

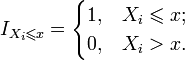
Статистика критерия для эмпирической функции распределения определяется следующим образом:

где  — точная верхняя грань множества , F - предполагаемая модель.

Критерий

Обозначим нулевую гипотезу , как гипотезу о том, что выборка подчиняется распределению . Тогда по теореме Колмогорова для введённой статистики справедливо:

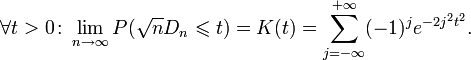
Учтём, что критерий имеет правостороннюю критическую область.

Правило (параметрический критерий Колмогорова). Если статистика превышает процентную точку распределения Колмогорова заданного уровня значимости , то нулевая гипотеза (о соответствии закону ) отвергается. Иначе гипотеза принимается на уровне .

Если α достаточно близко к 1, то можно приблизительно рассчитать по формуле:

Асимптотическая мощность критерия равна 1.

Обозначим теперь за нулевую гипотезу гипотезу о том, что две исследуемые выборки подчиняются одному распределению случайной величины .

Теорема Смирнова. Пусть — эмпирические функции распределения, построенные по независимым выборкам объёмом n и m случайной величины ξ. Тогда, если , то , где .

Теорема Смирнова позволяет использовать данный критерий для проверки двух выборок на однородность.

Правило (непараметрический критерий Колмогорова). Если статистика 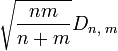превышает квантиль распределения Колмогорова заданного уровня значимости , то нулевая гипотеза (об однородности выборок) отвергается. Иначе гипотеза принимается на уровне .