Ответы на экзаменационные вопросы по теории вероятности + Экзаменационные вопросы / 29. Интервальное оценивание. Интервальные оценки математического ожидания и дисперсии

29. Интервальное оценивание. Интервальные оценки математического ожидания и дисперсии.

Интервальное оценивание — один из видов статистического оценивания, предполагающий построение интервала, в котором с некоторой вероятностью находится истинное значение оцениваемого параметра.

Определение:

Пусть  - неизвестный параметр генеральной совокупности. По сделанной выборке по определенным правилам находятся числа  и  такие чтобы выполнялось неравенство:

Интервал  является доверительным интервалом для параметра , а число  - доверительной вероятностью или надежностью сделанной оценки. Обычно надежность задается заранее, причем выбираются числа близкие к 1 (0.95, 0.99 или 0.999).

Интервальная оценка математического ожидания  при известной дисперсии

 

Итак, Х ~ N(а,σ) (случайная величина Х имеет нормальное распределение с параметрами а и σ), причем значение параметра а не известно, а значение дисперсии σ² известно.

При ~ эффективной оценкой параметра а является , при этом ~. Статистика 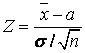 имеет распределениеN(0; 1) независимо от значения параметра а и как функция параметра а непрерывна и строго монотонна. Следовательно, с учетом неравенства (1.12) и симметричности двусторонних критических границ распределения N(0; 1) будем иметь:

Р(–u_а < Z < u_а) = 1 – α = γ.

Решая неравенство  относительно а, получим, что с вероятностью 1 – α выполняется неравенство:

,                              (1.13)

 

при этом:

 .                                              (1.14)

 

Число u_а находят по прил. 3 из условия Ф(u_а) = γ/2.

Замечание. Если п велико, оценку (1.13) можно использовать и при отсутствии нормального распределения величины Х, так как в силу следствия из центральной предельной теоремы при случайной выборке большого объема п

.

В частности, если Х = μ, где μ – случайное число успехов в большом числе п испытаний Бернулли, то

,

и с вероятностью ≈1 – α для вероятности р успеха в единичном испытании выполняется неравенство

 

.                         (1.15)

 

Заменяя значения р и q = 1 – р в левой и правой частях неравенства (1.15) их оценками  и , что допустимо при большом п,получим приближенный доверительный интервал для вероятности р:

                                         

< p < .                          (1.16)

 

Пример:  

Фирма коммунального хозяйства желает на основе выборки оценить среднюю квартплату за квартиры определенного типа снадежностью не менее 99 % и погрешностью, меньшей 10 д. е. Предполагая, что квартплата имеет нормальное распределение со средним квадратичным отклонением, не превышающим 35 д. е., найдите минимальный объем выборки.

Решение. По условию требуется найти такое п, при котором , где а и  – генеральная и выборочная средние.

Приравняв γ = 0,99, α = 1 – γ, из прил. 3 найдем число u_а, при котором Ф(u_а) = γ / 2 = 0,495; и_0,01 = 2,6. При ε = 10 и σ = 35 из формулы (1.14) получим 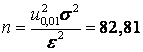. Но так как с ростом γ и уменьшением ε растет п, то п ≥ 82,81 и n_min = 83 (конечно, при уменьшении верхней границы для σ будет уменьшаться и n_min).