Ответы на экзаменационные вопросы по теории вероятности + Экзаменационные вопросы / 35. Определение случайной функции. Законы распределения. Числовые характеристики

35. Определение случайной функции. Законы распределения. Числовые характеристики.

Случайный процесс (случайная функция) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим рольвремени или координаты. Другое определение:

Случайным называется процесс u(t), мгновенные значения которого являются случайными величинами.

Определение:

Пусть дано вероятностное пространство . Параметризованное семейство случайных величин

,

где T произвольное множество, называется случайной функцией.

Если , то параметр может интерпретироваться как время. Тогда случайная

функция {Xt} называется случайным процессом. Если множество T дискретно, например , то такой случайный процесс называется случа́йной после́довательностью.

Если , где , то параметр может интерпретироваться как точка в пространстве, и тогда случайную функцию называют случа́йным по́лем.

Данная классификация нестрогая. В частности, термин "случайный процесс" часто используется как безусловный синоним термина "случайная функция".

Законы распределения:

∙Биномиальный закон.

∙Закон Пуассона.

∙Геометрическое распределение.

∙Гипергеометрическое распределение.

∙Равномерный закон.

∙Показательный (экспоненциальный) закон.

∙Нормальный закон.

∙Логарифмически-нормальное распределение.

∙Функция надежности.

Числовые характеристики:

Математическое ожидание — это число, вокруг которого сосредоточены значения случайной величины.

Если x — дискретная случайная величина с распределением то ее математическим ожиданием (обозначается Mx) называется величина, вычисленная по формуле

, если число значений случайной величины конечно, и по формуле

,если число значений случайной величины счетно. При этом, если ряд в правой части последнего равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей px (x) вычисляется по формуле

.

При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Если случайная величина h является функцией случайной величины x, h = f(x ), то

.

Аналогичные формулы справедливы для функций дискретной случайной величины:

, .

При вычислении математического ожидания случайной величины полезны следующие его свойства:

∙математическое ожидание константы равно этой константе, Mc = c;

∙математическое ожидание — линейная функция случайной величины, т.е. при произвольных постоянных a и bсправедливо: M(ax +bh ) = aMx + bMh;

∙математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(xh )=Mx Mh;

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина x имеет математическое ожидание Mx, то дисперсией случайной величины x называется величина .

Легко показать, что

.

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для

непрерывных. Величина Mx2 вычисляется по формулам , для дискретных и непрерывных случайных величин соответственно.

Еще одним параметром для определения меры разброса значений случайной величины является среднеквадратичное отклонение s x , связанное с дисперсией соотношением 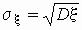. Перечислим основные свойства дисперсии:

∙дисперсия любой случайной величины неотрицательна, Dx >= 0;

∙дисперсия константы равна нулю, Dc = 0;

∙для произвольной константы D(cx ) = c2Dx ;

∙дисперсия суммы двух независимых случайных величин равна сумме их дисперсий, D(x ± h ) = Dx ± Dh .

Моменты:

В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются начальные и центральные моменты.

Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. .

Центральным моментом k-го порядка случайной величины x называется величина , определяемая формулой

.

Заметим, что математическое ожидание случайной величины — начальный момент первого порядка, , а дисперсия — центральный момент второго порядка, .

Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты. Одна из таких формул приведена выше: .

В дальнейшем будет использована формула

.

Нетрудно понять, что если плотность распределения вероятностей случайной величины симметрична относительно прямой x = Mx , то все ее центральные моменты нечетного порядка равны нулю.