Ответы на экзаменационные вопросы по теории вероятности + Экзаменационные вопросы / 15. Понятие моментов. Основные свойства

15. Понятие моментов. Основные свойства.

Моментслучайной величины —числоваяхарактеристика распределенияданнойслучайнойвеличины.

Еслиданаслучайная величина определённая нанекотором вероятностном пространстве, то: 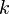-мначальныммоментом случайнойвеличины 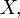где называетсявеличина

еслиматематическоеожидание вправойчастиэтогоравенства определено; -мцентральным моментом случайной величины 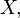называетсявеличина

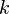-мабсолютными- мцентральным абсолютныммоментамислучайной величины называется соответственно величины

еслиматематическоеожидание вправойчасти этогоравенстваопределено.

Абсолютныемоментымогут бытьопределены нетолькодляцелых k,ноидлялюбыхположительныхдействительных вслучае, еслисоответствующиеинтегралы сходятся.

Основныесвойствамоментовслучайныхвеличин:

1)M[c] =∫ (c) f(x)dx=c∫f(x)dx=c

2)M[cx]=∫cxf(x)dx=c∫xf(x)dx=cMx

3)M[cx+k]= cMx+k

4)M[x1+x2+x3+...+Xn]=∑ Mx1

5)M[x1,x2,x3,...,xn]=∏ Mx1

6)D[c]=∫((c-m(c))^2) f(x)dx=∫((c-c)^2) f(x)dx=0

7)D[cx]= M[((cx-m(cx))^2)]=(c^2) Dx

8)D[x+-y]= Dx+Dy+-2M[x,y]