Ответы на экзаменационные вопросы по теории вероятности + Экзаменационные вопросы / 26. Понятие выборки. Вариационный ряд. Полигон частот. Выборочная функция распределения. Гистограмма

26. Понятие выборки. Вариационный ряд. Полигон частот. Выборочная функция распределения. Гистограмма.

Понятие выборки - одно из основных в комбинаторике, теории вероятностей и математической статистике, а подсчет числа выборок исторически был одной из первых задач комбинаторики. В типичных задачах по теории вероятностей подсчитывается число различных вариантов (выборок), а через них и вероятностей событий, связанных в большинстве случаев с бросанием монеты, кубика или со случайным выбором шаров из урны. Одним из первых занялся подсчетом различных комбинаций при игре в кости итальянский математик Тарталья. Приведем здесь одну из таких задач.

Пример 1. На какую сумму очков, выпадающих при подбрасываниях двух костей, разумно сделать ставку?

Решение. Перечислим возможные суммы и способы их получения.

2 = 1 + 1; 3 = 1 + 2 = 2 + 1; 4 = 1 + 3 = 3 + 1 = 2 + 2; 5 = 1 + 4 = 4 + 1 = 2 + 3 = 3 + 2;

6 = 1 + 5 = 5 + 1 = 2 + 4 = 4 + 2 = 3 + 3; 7 = 1 + 6 = 6 + 1 = 2 + 5 = 5 + 2 = 4 + 3 = 3 + 4;

8 = 2 + 6 = 6 + 2 = 3 + 5 = 5 + 3 = 4 + 4; 9 = 3 + 6 = 6 + 3 = 4 + 5 = 5 + 4;

10 = 4 + 6 = 6 + 4 = 5 + 5; 11 = 5 + 6 = 6 + 5; 12 = 6 + 6.

Откуда видно, что целесообразно сделать ставку на выпадение в сумме 7 очков, поскольку она получается наибольшим количеством вариантов, а, следовательно, имеет больше шансов на выпадение, чем другие суммы. Первоначально комбинаторные задачи касались в основном азартных игр - определения, сколькими способами можно получить данное число очков, бросая несколько костей, как в предыдущем примере, или сколькими способами можно получить тот или иной набор карт. Размышления над анализом азартных игр явились движущей силой в развитии комбинаторики и развивавшейся одновременно с ней теорией вероятностей. Такой подход логично продолжить и для рассмотрения современных игр.

Вариационный ряд

Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины:

равные между собой элементы выборки нумеруются в произвольном порядке; элементы вариационного ряда называются порядковыми (ранговыми) статистиками; число λ_m =m / n называется рангом порядковой статистики 

Вариационный ряд используется для построения эмпирической функции распределения. Если элементы вариационного ряда независимы и имеют общую плотность распределения f, то совместная плотность распределения элементов вариационного ряда имеет вид:

Полигон частот и гистограмма

Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки . Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты  и соединяют точки отрезками прямых.

Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты .

В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала  – сумму частот вариант, попавших в i–й интервал.

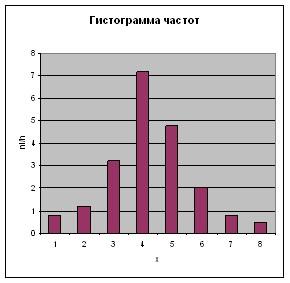
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению . Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте) . Площадь i–го прямоугольника равна  – сумме частот вариант i–о интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

В случае гистограммы относительных частот по оси ординат откладываются относительные частоты , на оси абсцисс – частичные интервалы, над ними проводят отрезки, параллельные оси абсцисс на высоте . Площадь i–го прямоугольника равна относительной частоте вариант , попавших в i–й интервал. Поэтому площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.

Выборочная функция распределения:

Выборочная (эмпирическая) функция распределения в математической статистике - это приближение теоретической функции распределения, построенное с помощью выборки из него.

Пусть  - выборка из распределения случайной величины , задаваемого функцией распределения . Будем считать, что , где , -независимые случайные величины, определённые на некотором пространстве элементарных исходов Ω. Пусть . Определим случайную величину следующим образом:

,

где  - индикатор события ,  - функция Хевисайда. Таким образом, выборочная функция распределения в точке  равна относительной частоте элементов выборки, не превосходящих значение . Случайная величина  называется выборочной функцией распределения случайной величины  и является аппроксимацией для функции . Существует результат, показывающий, что при  функция  равномерно сходится к , и указывающий скорость сходимости.