Ответы на экзаменационные вопросы по теории вероятности + Экзаменационные вопросы / 24. Неравенство Чебышева. Теорема Чебышева (обобщения)

24. Неравенство Чебышева. Теорема Чебышева (обобщения).

.

Неравенство:

На практике сложно сказать какое конкретное значение примет случайная величина, однако, при воздействии большого числа различных факторов поведение большого числа случайных величин практически утрачивает случайный характер и становится закономерным.

Этот факт очень важен на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов.

Однако, это возможно только при выполнении некоторых условий, которые определяются законом больших чисел. К законам больших чисел относятся теоремы Чебышева (наиболее общий случай) и теорема Бернулли (простейший случай), которые будут рассмотрены далее.

Требуется определить вероятность того, что отклонение значения случайной величины от ее математического ожидания будет не больше, чем заданное число e.

Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше чем .

Пусть случайная величина определена на вероятностном пространстве 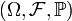, и её математическое ожидание μ и дисперсия σ2 конечны. Тогда

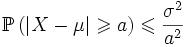, где a > 0.

Если a = kσ, где σ — стандартное отклонение и k > 0, то получаем

.

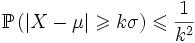В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на 2 стандартных отклонения с вероятностью меньше 25%. Она отклоняется от среднего на 3 стандартных отклонения с вероятностью меньше 11,2%.

Теорема:

Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное числоe, вероятность неравенства

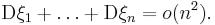
будет сколь угодно близка к единице, если число случайных величин достаточно велико.

Т.е. можно записать: 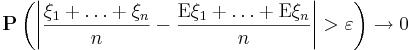(при любом 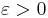и 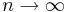) верно при весьма общих предположениях:

Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:

Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины.

Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.

Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.

Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.