15. Теорема об изменении кинетической энергии системы.

- теорему об изменении кинетической энергии в конечном виде: изменение кинетической энергии системы при некотором ее конечном перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил.

Составляя такие уравнения для всех точек системы и складывая их почленно получаем:

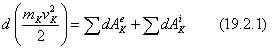
16. Принцип Даламбера для точки и механической системы. Главный вектор и главный момент сил инерции.

Принцип Даламбера для точки:Принцип Даламбера для материальной точки сводится к следующему утверждению: если к силам, действующим на материальную точку, условно присоединить силу инерции точки, то получим уравновешенную систему сил, т. е.

Главный вектор и главный момент сил инерции твёрдого тела.

главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

17. Число степеней свободы. Возможные перемещения. Идеальные связи.

Число независимых координат, которые однозначно определяют положение тела или системы тел в пространстве называется числом степеней свободы.

При идеальных связях,

Связи являются идеальными, если сумма работ сил реакций на возможны перемещениях равняется нулю.

18. Принцип возможных перемещений.

Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех активных сил на всех возможных перемещениях была равна нулю.

В проекциях на оси координат уравнение (20.2.7) запишется:

19. Общее уравнение динамики.

Объединяя принцип Даламбера и принцип возможных перемещений, получим общеe уравнение динамики:

Из этого уравнения вытекает следующий принцип Даламбера-Лагранжа: при движении системы с идеальными связями в каждый данный момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю.