6. Векторный, координатный и естественный способы задания движения точки. Определение скорости и ускорения точки при различных способах задания движения.

Координатный способ – зависимость координат от времени

Векторный способ задания движения.

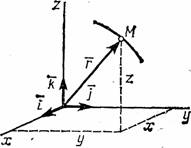
Пусть задана система отсчета Oxyz (рис. 43 ).

Положение точки М в ней, в любой момент времени можно определить, задав вектор r из точки О в точку М. Такой вектор называется радиус-вектором точки М. С течением времени он изменяется, то есть

Это и есть закон движения точки в векторной форме. Годограф этого вектора определяет траекторию движения точки.

Координатный способ задания движения.

Положение точки по отношению к данной системе отсчета O,x,y,z можно определить с помощью координат x,y,z (рис. 42 ). При движении точки М вдоль траектории, с течением времени, координаты будут изменяться и чтобы задать закон движения точки, нужно задать зависимости:

Соотношения (8.2.2) представляют собой уравнения движения точки в декартовых прямоугольных координатах. Они представляют собой и параметрические уравнения траектории. Исключив параметр t, получим уравнение траектории через координаты.

Естественный способ задания движения.

Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. В зависимости от вида траектории движение называют прямолинейным или криволинейным.

Пусть O1, x1 y1 z1 - система отсчета; АВ - траектория; О - начало отсчета; (+-) - направление движения; S - криволинейная координата или расстояние вдоль дуги с соответствующим знаком (рис. 41 ).

Так как точка М движется вдоль траектории, то ее координата S будет изменяться со временем, то есть

S = f(t) (8.2.1)

Это и есть закон движения точки М вдоль траектории. Таким образом, чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки. 2) начало отсчета на траектории с указанием направления движения (), 3) закон движения точки вдоль траектории в виде (8.2.1).

Здесь необходимо заметить, что S определяет положение точки на траектории, а не пройденный путь.

7. Поступательное движение твердого тела. Траектории, скорости и ускорения точек твердого тела при поступательном движении.

Поступательным движением твердого тела называется такое его движение, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению во все время движения.

Теорема. При поступательном движении твердого тела все его точки движутся по одинаковым и параллельным траекториям и имеют в каждый данный момент времени равные по модулю и направлению скорости и ускорения.

8. Вращение твердого тела вокруг неподвижной оси. Уравнение вращательного движения твердого тела. Угловая скорость и угловое ускорение тела. Скорость и ускорение точек твердого тела, вращающегося вокруг неподвижной оси.

Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все его точки, лежащие на некоторой прямой, называемой осью вращения, все время остаются неподвижными.

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П0 и П , одна из которых неподвижна, а другая жестко связана с телом.

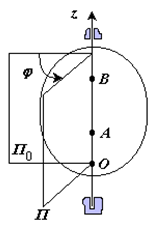
φ=φ(t) – уравнение вращательного движения твердого тела

Угловой скоростью - называется векторная величина, равная первой производной угла поворота тела по времени:

Угловым ускорением - называется векторная величина, равная первой производной yгловой скорости по времени:

Равномерное вращение

Фи=wt – угол поворота (расстояние)

Равноускоренное (равнопеременное)

W=w0+Et – угловая скорость

Фи=W0t + Et^2/2 – угол поворота

9. Плоскопараллельное движение твердого тела. Уравнения плоского движения тела. Определение скорости любой точки твердого тела при плоском движении. Теорема о проекциях скоростей двух точек фигуры. Мгновенный центр скоростей, определение с его помощью скоростей точек плоской фигуры.

Плоскопараллельное движение – это движение твердого тела параллельно некоторой фиксированной плоскости.

Уравнения, определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твер¬дого тела.

X0=f1(t)

Y0=f2(t)

Фи=f3(t)

Первые два из уравнений движения определяют то движение, которое фигура совершала бы при фи =const; это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А.

Когда полюс А неподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.

Теорема о проекциях скоростей двух точек тела

Определение скоростей точек плоской фигуры (или тела, дви­жущегося плоскопараллельно) связано обычно с довольно сложными расчетами. Однако можно получить ряд других, практически более удобных и простых мето­дов определения скоростей точек фигуры (или тела).

Рис.32

 

Один из таких методов дает тео­рема: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу. Рассмотрим какие-нибудь две точкиА и В плоской фигуры (или тела). Принимая точкуА за полюс (рис.32), получаем . Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор перпендику­лярен АВ, находим

итеоремадоказана.

МЦС – это точка твёрдого тела непосредственно с ней связанна, скорость который в данный момент времени равна 0.

Твёрдое тело совершает вращательное движение относительно МЦС.

V = w * R (угл.Скорость на путь от точки до МЦС)

W = V/R