ВОПРОСЫ ПО МЕХАНИКЕ
Основные понятия и аксиомы статики.
Статика – изучает равновесие тел под действием сил.
Абсолютно твердое тело - эти тело не деформируются, не изменяют свою форму и объем, какое бы действие на них не было оказано
Материальная точка – тело размерами которого можно пренебречь в данных условиях
Сила характеризуется :
Направлением
Точкой приложения
Величиной (сила –векторная величина )
Силой называется количественная мера механического взаимодействия тел. Сила является векторной величиной, действие силы на тело определяется численным значением (модулем), направлением и точкой приложения силы
Система сил = 0 или уравновешена если под действием этой силы тело находится в покое
Линия действия силы – линия вдоль которой действует сила
Аксиомы
1) 2 силы уравновешены если они лежат на одной прямой , равны по величине и противоположны по направлению
2) Действие силы не изменяется если перенести её по линии действия силы
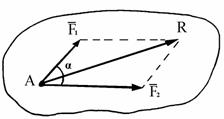
3) Равнодействующая двух сил, приложенных к АТТ в одной точке, равна
их геометрической сумме, т.е. выражается по моду-лю и направлению диагональю параллелограмма,построенного на этих силах.
4) 2 тела взаимодействуют друг с другом силами равными по величине и противоположными по направлению
Или
Всякому действию одного тела на другое соответствует равное по величине,
но противоположное по направлению противодействие. Действие и противодействие-это силы, приложенные к двум раз-личным телам, поэтому они не уравновешиваются
5) Аксиома затвердевания
Деформируемое тело можно рассматривать как абсолютно твердое
Или
Если деформируемое тело под действием системы сил находится в
равновесии, то при отвердевании его равновесие сохраняется.
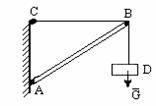
Под действием сил тело D находится в равновесии. Если трос CB заменить стержнем,
то равновесие не нарушится, равновесие не нарушится и в том случае, если трос BDза-менить стержнем, если же стержень АВ заменить тросом - равновесие нарушится
6) Освобождаемость.
Любое несвободное тело можно считать свободным, если заменить связь силой реакции связи.
Свободное тело – движется неограниченно
Не свободне – ограничено
2. Основные виды связей и их реакции. Геометрический и аналитический способы сложения сил.
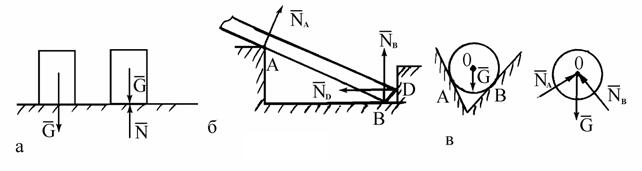
1) Гадкая поверхность или опора
Реакция связи всегда направлена в противоположную сторону возможного движения
2) Нить или невесомый стержень
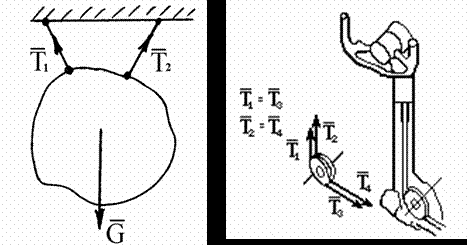
Если нить отклоняется роликом, в котором не учитывается трение, то натя-жение нити не изменяется
3) Шарниры
Шарниром в механике называется устройство, до-пускающее поворот одного тела
относительно другого, но ограничивающее при этом линейные перемещения этих тел.
Реакция цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси шарнира. Направление реакции зависит от ве-личины и направления действующих на тело сил. Реакция подвижного шарнира всегда направлена по нормали к опорной поверхности шарнира
Шаровой шарнир исключает любое перемещение тела во всех направле-ниях, кроме вращения, поэтому
реакция шарового шарнира может иметь любое направление в пространстве. Чаще всего эту реакцию
представляют в виде трех ее составляющих по осям координат
Геометрический способ
Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил , , …, (рис. 14, a), откладываем от произвольной точки О (рис. 14, б) вектор Oa, изображающий в выбранном масштабе cилу F1, от точки a откладываем вектор , изображающий силу F2, от точки b откладываем вектор bc, изображающий силу F3 и т. д.; от конца m предпоследнего вектора откладываем вектор mn, изображающий силу Fn. Соединяя начало первого вектора с концом последнего, получаем вектор = , изображающий геометрическую сумму или главный вектор слагаемых сил:
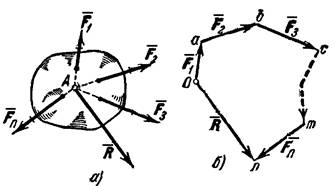
R=F1+F2…+Fn(вектора)
От порядка, в котором будут откладываться векторы сил, модуль и направление не зависят. Легко видеть, что проделанное построение представляет собою результат последовательного применения правила силового треугольника.
Главное условие равновесия – замкнутость силового многоугольника.
Аналитический способ
Аналитический от слова - анализ, то есть разложение вектора. Выбираем некоторую систему координат, желательно прямоугольную. Каждый вектор представляем в виде совокупности его координат в этой системе. Сумма векторов представляется как сумма координат слагаемых.
R= корень Rx^2+Ry^2+Rz^2
Условия равновесия
Rx= SumFkx=0
Ry=SumFky=0
Rz=SunFkz=0