Семинар 2. ТвиМС1. 21.02.04

Геометрическая вероятность

Пусть –ограниченное множество n-мерного евклидова пространства. Будем предполагать, что  имеет объем. Рассмотрим систему подмножеств множества . Для любого A положим

P{A}= ,

где (С)–объем множества С. Если под объемом множеств понимать его меру Лебега, то система множеств – это -алгебра измеримых по Лебегу множеств, и тогда функция P{A} является вероятностью. Отметим, что система , в частности, содержит все подмножества , измеримые по Жордану. В большинстве задач рассматривается именно этот частный случай.

Задачи

1. Какова вероятность того, что сумма двух случайно взятых положительных чисел, каждое из которых не больше единицы, не превзойдет единицы, а их произведение будет не больше . Ответ: .

2. В любые моменты времени промежутка T равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше . Определить вероятность того, что приемник забит.

Указание. Пусть x, y–моменты поступления сигнала в приемник. Приемник забит, если | x– y |. Ответ: p=1–.

3. На квадрат ={ (u, v): 0u1, 0v1} брошена точка. Найти вероятность того, что точка будет удалена от центра не больше чем на . Ответ: /4.

4. На горизонтальной плоскости вдоль прямой AB через интервал l расположены оси одинаковых вертикальных цилиндров с радиусом основания r. Под углом  к прямой бросается шар радиуса R. Определить вероятность столкновения шара с цилиндром, если пересечение линии движения центра шара с прямой AB равновозможно в любой точке.

Ответ:

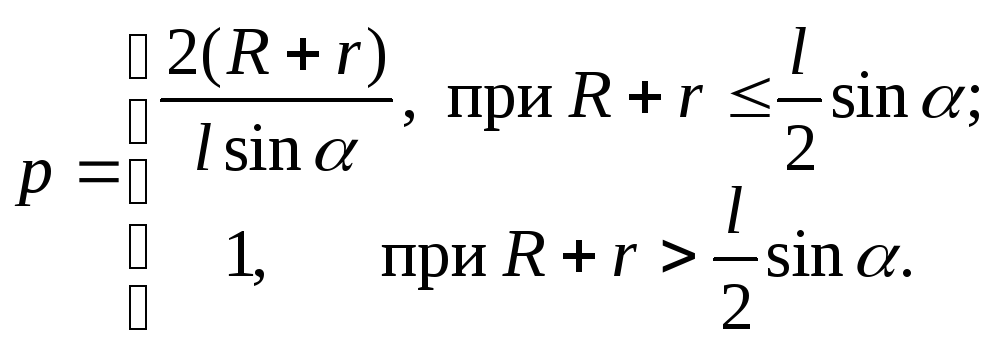
5. Коэффициенты p и q квадратного уравнения x²+px+q=0 выбираются случайно из промежутка (0, 1). Найти вероятность того, что корни будут действительными числами. Ответ: 1/12.

6. Два лица имеют одинаковую вероятность прийти к указанному месту в любой момент промежутка времени T. Определить вероятность того, что время ожидания одним другого будет не больше t. Ответ: p=1–.

7. Дуэли в городе Осторожности редко кончаются печальным исходом. Дело в том, что каждый дуэлянт прибывает на место встречи в случайный момент времени между 5 и 6 часами и, прождав соперника 5 минут, удаляется. В случае же прибытия последнего в эти пять минут дуэль состоится. Какая часть дуэлей действительно заканчивается поединком? Ответ: 1/6.

8. На отрезке длиной l случайно выбраны две точки. Какова вероятность, что расстояние между ними будет меньше kl, 0<k<1. Ответ: k(2–k).

9. На отрезке AB длиной l случайно поставлены две точки L и M. Найти вероятность того, что точка L будет ближе к точке M, чем к точке A. Указание: x=AL, y=AM. Возможные значения 0x+ y  l. Благоприятные значения: | y– x|x. Ответ: p=0,75.

10. На отрезке длиной l случайно поставлены две точки, в результате чего этот отрезок оказывается разделенным на три части. Найти вероятность того, что из трех получившихся частей можно построить треугольник. Указание: x, y– два отрезка. Возможные значения 0x+ yl. Благоприятные значения: xl/2, yl/2, x+yl/2. Ответ: p=1/4.

11.Монета упала на дощатый пол. Ширина доски 2H, радиус монеты r (2r<2H). Какова вероятность того, что монета попадет на щель? Указание. Положить ={u: 0uH }; u –расстояние от центра монеты до ближайшего края доски. Ответ: 2/H.

12. В задаче 11 рассмотреть случай более узкой доски, когда H< r<2H. Найти вероятность, что монета накроет k щелей (k =1, 2). Ответ: 1) , k =1; 2) , k =2.

13. Пассажир может ехать на любом из автобусов двух маршрутов, следующих с интервалами T₁, T₂. Момент прихода пассажира определяют на отрезках [0, T₁], [0, T₂] точки u, v, равные времени, оставшемуся до прихода трамвая соответствующего маршрута. Предполагая, что точка (u, v) равномерно распределена на ={(u, v): 0uT₁, 0vT₂}, найти вероятность того, что пассажир, пришедший на остановку, будет ждать не больше t (0<t<min(T₁, T₂)). Указание. Благоприятное событие описывается подмножеством {(u, v): min(u, v)t}. Ответ: .

14. На окружности радиуса R случайно поставили три точки A, B, C. Найти вероятность, что треугольник ABC остроугольный. Указание. Две дуги x, y. Возможные значения 0 x+y2R. Благоприятные значения: xR, yR, x+yR. Ответ: p=1/4.

15. Найти вероятность, что из трех взятых случайно отрезков длины не более l можно построить треугольник. Ответ: p=1/2.

16. На паркет, составленный из правильных k-угольников, со стороной a, случайно бросается монета радиуса r. Найти вероятность того, что упавшая монета не заденет границу ни одного из k-угольников для а) k=3; б) k=4; в) k=6. Указание. Центр монеты можно считать равномерно распределенным в том k-угольнике, в которой он попал.

Ответ: , если r< ; 0 при r, k=3, 4, 6 .

17. Задача Бюффона. На дощатый пол упала игла. Ширина доски–2L, длина иглы–2l, (l<L). Найти вероятность того, что игла пересечет щель. Указание. В качестве элементарного события можно взять точку (, u): u – расстояние середины иглы до ближайшей щели, – угол наклона иглы. Тогда ={(, u): 0, 0 u L}. Ответ: 2l/L.

18. Парадокс Бертрана. В круге радиуса R случайно проводится хорда. Обозначим  ее длину. Найти вероятность Q_x=P{>x} и вычислить вероятности и того, что длина хорды больше стороны правильного вписанного шестиугольника и треугольника соответственно, если: а) середина хорды равномерно распределена в круге; б) направление хорды задано, а ее середина равномерно распределена на диаметре, перпендикулярном ее направлению; в) один конец хорды закреплен, а другой равномерно распределен на окружности.

Вероятность Q_x зависит от интерпретации слова «случайно», и числовые значения различны в случаях а), б), в). Указание. Пусть (,) –полярные координаты середины хорды. Выразить  через R и . Ответ: а) Q_x=; б) Q_x=, в) Q_x= .