
Решения / 9 семинар
.doc
Семинар №9 «Характеристики случайных величин. Математическое ожидание. Дисперсия. II» (1 из 9) |
Семинар №9 «Характеристики случайных величин. Математическое ожидание. Дисперсия. II» (2 из 9) |
|
1. Случайная величина задана функцией распределения:
Найти E, D. Ответ: 3a/2, 3a2/4. Решение:
2.
Случайная величина
имеет показательное распределение
((x)= Решение:
а)
б)
в)
|
3. Плотность распределения с.в. имеет вид (x)=c(x2 +x+1), если 0x1, и (x)=0 –иначе. Найти E, D. Ответ: 13/22, 189/2420. Решение:
4. Найти E, D случайной величины , равномерно распределенной на [a, b]. Ответ: (a+b)/2; (b– a)2/12. Решение:
5.
Найти E,
D
случайной величины ,
имеющей нормальное распределение с
параметрами a
и 2
(
|
Семинар №9 «Характеристики случайных величин. Математическое ожидание. Дисперсия. II» (3 из 9) |
Семинар №9 «Характеристики случайных величин. Математическое ожидание. Дисперсия. II» (4 из 9) |
|
Указание:
замена переменных y=(x–a)/,
и Решение:
Замена:
6. Случайная величина равномерно распределена на [0,1]. Найти E3. Ответ: 1/4. Решение:
7. Плотность распределения с.в. имеет вид (x)=2x, если 0<x<1, 0– иначе. Найти E5 , D5. Ответ: 2/7, 25/294. Решение:
|
8.
Случайная величина
имеет нормальное распределение с
параметрами a=0 и
2=1. Найти а)
E||;
б) Ek,
k=1,2,… Указание: Вывести рекуррентную
формулу для Ek,
используя интегрирование по частям
. Ответ:
Решение:
9.
Плотность распределения с.в.
имеет вид (x)= Решение:
|
Семинар №9 «Характеристики случайных величин. Математическое ожидание. Дисперсия. II» (5 из 9) |
Семинар №9 «Характеристики случайных величин. Математическое ожидание. Дисперсия. II» (6 из 9) |
|
10.
Плотность распределения с.в.
имеет вид (x)=xne–x/n!
при x0,
(x)=0
при x<0. Найти E,
D.
Указание:
Решение:
11. Пусть x– непрерывная случайная величина с плотность распределения rx(x) на отрезке [a, b], rx(x)=0 вне отрезка. Доказать, что a£Ex£b. Решение:
Док-ть:
|
12.
Случайная
величина x
имеет конечный второй момент Ex2.
Найти
Решение:
13. Будем говорить, что случайная величина сосредоточенна на отрезке [a, b], если P{a£x£b}=1 и при любом e>0 P{a£x<a+e}>0, P{b–e<x£ b}>0. Доказать, что дисперсия случайной величины, сосредоточенной на отрезке длины l, не превосходит l2/4. Указание:
Пусть P{a£x£b}=1,
b–
a=l.
Воспользоваться тем, что Dx£ Решение:
Треб док-ть:
|
Семинар №9 «Характеристики случайных величин. Математическое ожидание. Дисперсия. II» (7 из 9) |
Семинар №9 «Характеристики случайных величин. Математическое ожидание. Дисперсия. II» (8 из 9) |
|
14.
Показать, если x–
действительная случайная величина с
конечным математическим ожиданием и
f(x)
– функция, выпуклая вниз, то
Решение: Нет решения 15.
Случайные величины x
и h
имеют равномерное распределение на
отрезке [0, 1]. Доказать, что при любом
характере зависимости между x
и h
выполняется неравенство
Решение:
|
16. Показать, что для любых случайных величин x1,…, xk с конечными r-ми (r³1) моментами справедливо соотношение
Указание: Использовать выпуклость вниз функции f(x)=| x|r и зад. 14. Решение:
17.
Из урны, содержащей m
белых и
n–m
черных шаров c
возвращением извлекают b
шаров. Пусть с.в. x–
число белых шаров среди извлеченных.
Найти Ex,
Dx.
Ответ:
Решение: m-белых,
(n-m)-черных,
b
шаров извл с возвр,
18.
Из урны, содержащей m
белых и
n–m
черных шаров без возвращения извлекают
b
шаров. Пусть с.в. x–
число белых шаров среди извлеченных.
Найти Ex,
Dx.
Указание: Случайная величина hi=1,
если i-й
шар белый, и hi=0,
если i-й
шар черный. x=h1+…+hb.
(проверить) Dhj=
|
Семинар №9 «Характеристики случайных величин. Математическое ожидание. Дисперсия. II» (9 из 9) |
|
|
Решение: m-белых,
(n-m)-черных,
b
шаров извл без возвр,
|
|





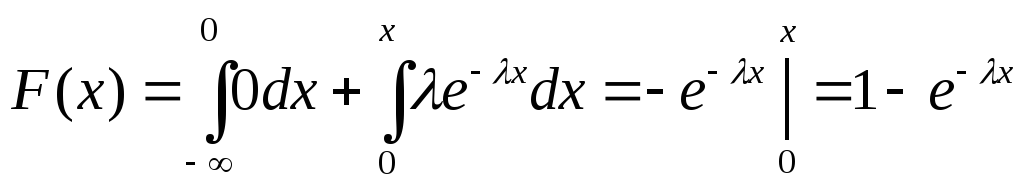

 ,
,


 ,
–<x<+).
,
–<x<+).
 ,
,
 .
Ответ: a,
2.
.
Ответ: a,
2.

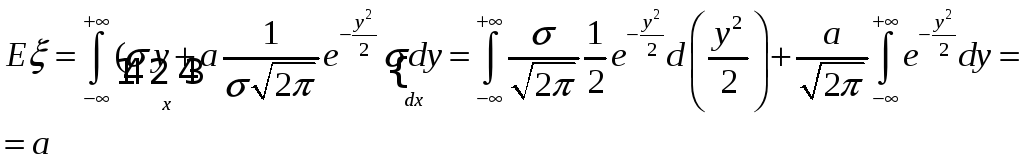



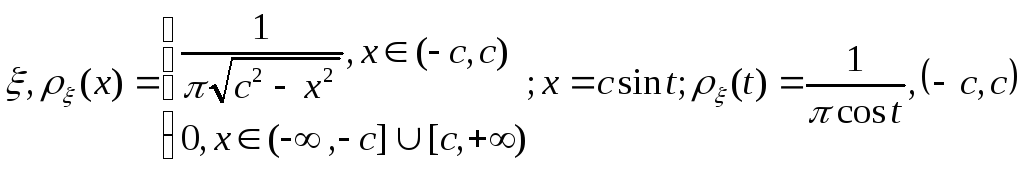


 ,
,







