11.Методы обнаружения автокорреляции
Если
сущ-ет корреляция ошибок εt,
то она присутствует и в остатках модели
et.
H0
сост. в отсутствии автокорреляции:
,
.
Автокор-я опр-ся как кор-я м/у наблюд-ми
показат-ми, упорядоч-ми во времени или
пр-ве.
1.Граф-й м-д: указывает отклон-я et с мом-ми t их получ-я. строятся послед-но времен-е графики. В посл. случ. отсут-ет автокор-ия.
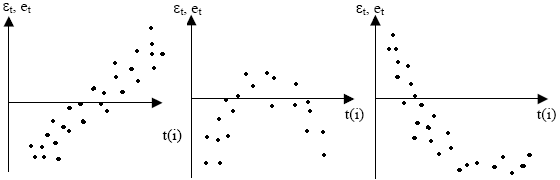
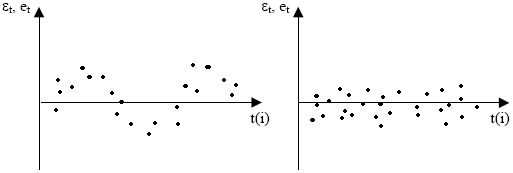
2.М-д рядов: послед-но опред-ся знаки отклонений et.
Пр-р: (-----)(+++++++++)(---)(++++) Ряд опр-ся как непрерыв.послед-ть одинаков.знаков. Кол-во знаков в ряду–длина ряда. Если рядов слишком мало по сравнению с кол-вом наблюд-й, то м.говорить о полож.автокор-и. Если много, то вероятно отриц-я. Для анализа предлаг-ся процедура:
n-число набл-й выборки (V выборки); n1-общее число «+» в n-набл-иях; n2-число «-» в n-набл-иях; к-число рядов.
При достато-чно большом n (n1>10, n2>10) и отсутствии автокор-и СВ k имеет норм.распр-е с матожид-ем M(k)=((2n1n2)/(n1+n2)) +1 и дисперсией D(k)=(2n1n2(2n1n2-n1-n2))/((n1+n2)²(n1+n2-1))
Тогда если M(k)-Uα/2D(k)<k<M(k)+Uα/2D(k), то гипотиза об отсуттствии автокоррел-и не отклоняется. Величины Uα/2 затабулированы. При небольш. n (n1<20,n2<20) разраб-ы табл. На пересеч. n1 и n2 опред-ы к1 и к2. Если к1<k<k2 – отсутс. автокор. Если к ≤ к1 – полож. автокор. Если к ≥ к2 – отриц. автокор.
12.Тест Дарбина-Уотсона
Наиболее известным критерием обнаружения автокорреляции первого порядка является критерий DW (критерий Дарбина-Уотсона).
На практике исп-ся ст-ка DW: DW=∑(et-et-1)2/∑et2 ≈ 2(1-r)
Если м/ду сосед.остатками им-ся достаточно высок.полож.кор-ия, то в опред.смысле эти ост-ки близки др.к др. (r ≈ 1) и ст-ка DW мала (→ 0), а если сущ-ет отриц.автокор-ия (r ≈ -1), то ст-ка DW→ 4. Если автокор-я отсуь-ет (r ≈ 0), то DW ≈ 2. Для более точного опред-я исп-ют табл. Критич.зн-ия ст-ки зав-т от числа наблюдений n, количества объясняющих переменных m, заданного уровня значимости α. По табл. опред-ют 2 границы: ниж.и верх., к-ые зав-т тодько от n,m,α (dL и dU). Если оценен.ст-ка DW нах-ся в пределах:
4-dL ≤ DW ≤ 4, H0 отверг-ся, есть отриц.кор-ия; 4-dU ≤ DW < 4-dL, неопред-ть; dU ≤ DW < 4-dU, H0 не отверг-ся, автокор-ия отсут-ет;
dL ≤ DW < dU, неопред-ть; 0 ≤ DW<dL, H0 отверг-ся, есть полож.кор-ия
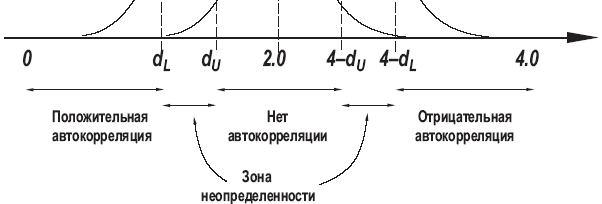
С ростом числа набл-ий зона неопред-ти суж-ся.
Замеч-ия: 1.Ст-ка DW прим-ся для моделей, к-ые сод-т своб.член; 2.Случ. откл-я опред-ся авторегрес.схемой 1-го порядка:
εt = ρεt-1 + vt, где vt – случ. член;
3.Стат.данные д.им.одинак.период-ть (не д.б.пропусков);
4.Критерий DW не прим-ся для регрес.моделей, сод-щих в составе объясняющ.пер-ную с времен.лагом в один пер-д, т.е. для авторегрес-ых моделей вида: yt = β0 +β1 xt1+ …+βmxtm+γYt-1+εt
13. Оценивание в модели с автокорреляцией.
Значение коэф-та кор-ии ρ известно. Рассм. модель парной лин. рег-ии: Y = β0+ β1X+ ε . Тогда набл-ям t и (t-1) соотв-ют ф-лы: yt= β0 + β1xt+εt (1) и yt-1= β0 + β1xt-1+εt-1 (2). Пусть случ.откл. подвержена автокор-ии 1-го пор-ка: εt=ρεt-1+vt и удов-ет всем предпос. МНК. Вычтем из (1) соотн-е (2), емнож-е на ρ: yt-ρyt-1= β0(1- ρ)+ β1(xt-ρ xt-1)+(εt+ρεt-1). (3) Положив yt-ρyt-1=ỹt; xt-ρ xt-1=x t̃; β0(1- ρ)= ^β0, получим: ỹt=^β0 + β1x t̃+ vt, t=2,n. Т.к ρ известен, то ỹt ,x t̃, vt вычисл-ся просто. К этому ур-ию прим-ся МНК и получ.оценки коэф-та регр-ии. Однако происх-ит потеря 1-го набл-я, число степ. своб. умен. на ед. и при малых выборках может привести к потере эф-ти.
Для того, чтобы исп-ть 1-ое ур-ие, след.сделать поправку Прайса-Викстона: x t̃=√(1-ρ2) *x1; ỹt=√(1-ρ2) *y1 : √(1-ρ2) *y1=√(1-ρ2) *x1β+√(1-ρ2) ε1
Однако на практике знач. ρ обычно неизвестно =>
1) Процедура Кохрейна-Оркатта
На нач.этапе к регр-ии прим-ся МНК и нах-ся век-р ост-ков: e=(e1,…,en).
1.В кач-ве приближ.оценки коэф-та кор-ии ρ берется его МНК-оценка в регр-ии: et=ρet-1+vt
2.Провод-ся
преобр-ие
.
Из-за потери первого набл-я провод-т
поправку Прайса-Викстона
.
Нах-ся
МНК-оценки исх.модели пар-ра β.
3.Строится нов.вектор остатков: e=y-xβˆ
4.Процедура повтор-ся снова с п.1. Точка останова – стабилизиров. зн-ие ρ или заранее опред-ое число итераций.