Семинар 9. ТВиМС1.

Теоремы Пуассона и Муавра-Лапласа

Пусть _n– число успехов (или число единиц) в n испытаниях Бернулли,

, k=.

Теорема Пуассона. Если n и p0 так, что np (0<<), то при любом k (k =0, 1,...)

.

В схеме Бернулли вероятность события {k₁_n k₂} вычисляется по формуле

.

При «больших» n и таких p, что npq «достаточно велико», можно использовать приближенную формулу для вычисления вероятности, основанную на следующей теореме.

Теорема Муавра-Лапласа. Пусть a, b, p, 0<p<1, фиксированные числа. Тогда

.

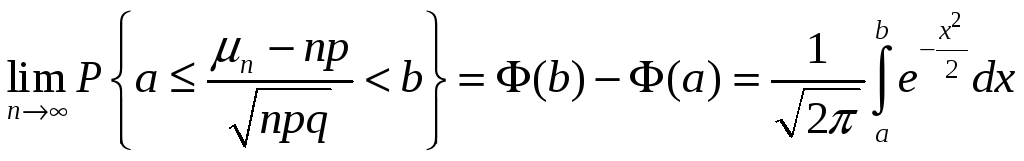где – функция нормального распределения с параметрами (0, 1),

Задачи

1. Случайная величина  задана функцией распределения:

Найти E, D. Ответ: 3a/2, 3a²/4.

2. Случайная величина  имеет показательное распределение (_(x)= при x0, 0 при x <0). Найти а) функцию распределения; б) P{^–1<<2^–1}; в) E, D. Ответ: 1–e^–x при x0, (1–e^–1)e^–1 , 1/, 1/².

3. Плотность распределения с.в.  имеет вид _(x)=c(x² +x+1), если 0x1, и _(x)=0 –иначе. Найти E, D. Ответ: 13/22, 189/2420.

4. Найти E, D случайной величины , равномерно распределенной на [a, b]. Ответ: (a+b)/2; (b– a)²/12.

5. Найти E, D случайной величины , имеющей нормальное распределение с параметрами a и ² (, –<x<+). Указание: замена переменных y=(x–a)/, и, . Ответ: a, ².

6. Случайная величина  равномерно распределена на [0,1]. Найти E³. Ответ: 1/4.

7. Плотность распределения с.в.  имеет вид _(x)=2x, если 0<x<1, 0– иначе. Найти E⁵ , D⁵. Ответ: 2/7, 25/294.

8. Случайная величина  имеет нормальное распределение с параметрами a=0 и ²=1. Найти а) E||; б) E^k, k=1,2,… Указание: . Ответ: , 0.

9. Плотность распределения с.в.  имеет вид _(x)= в интервале (–c, c), _(x)=0 вне интервала. Найти E, D. Указание: замена x=csin t. Ответ: 0, c²/2.

10. Плотность распределения с.в.  имеет вид _(x)=xⁿe^–x/n! при x0, _(x)=0 при x<0. Найти E, D. Указание: – гамма функция, , n–натуральное. Ответ: n+1, n+1.

11. Пусть – непрерывная случайная величина с плотность распределения _(x) на отрезке [a, b], _(x)=0 вне отрезка. Доказать, что aEb.

12. Случайная величина  имеет конечный второй момент E².

Указание: Воспользоваться равенством (доказав его) E(–x)²= E(–E)²+(x–E)².

13. Будем говорить, что

Указание: Пусть P{ab}=1, b– a=l. Воспользоваться тем, что D.

14.

15.

Плотность распределения с.в.  имеет вид _(x)=cx, если 0<x<2, 0– иначе. Найти E, D.