Семинар 9. ТВиМС1. Характеристики случайных величин. Математическое ожидание. Дисперсия. II

Задачи

1. Случайная величина  задана функцией распределения:

Найти E, D. Ответ: 3a/2, 3a²/4.

2. Случайная величина  имеет показательное распределение (_(x)= при x0, 0 при x <0). Найти а) функцию распределения; б) P{^–1<<2^–1}; в) E, D. Ответ: 1–e^–x при x0, (1–e^–1)e^–1 , 1/, 1/².

3. Плотность распределения с.в.  имеет вид _(x)=c(x² +x+1), если 0x1, и _(x)=0 –иначе. Найти E, D. Ответ: 13/22, 189/2420.

4. Найти E, D случайной величины , равномерно распределенной на [a, b]. Ответ: (a+b)/2; (b– a)²/12.

5. Найти E, D случайной величины , имеющей нормальное распределение с параметрами a и ² (, –<x<+). Указание: замена переменных y=(x–a)/, и, 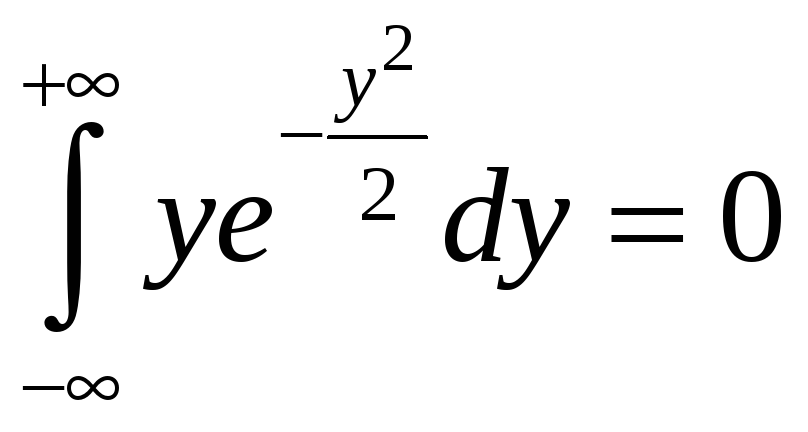. Ответ: a, ².

6. Случайная величина  равномерно распределена на [0,1]. Найти E³. Ответ: 1/4.

7. Плотность распределения с.в.  имеет вид _(x)=2x, если 0<x<1, 0– иначе. Найти E⁵ , D⁵. Ответ: 2/7, 25/294.

8. Случайная величина  имеет нормальное распределение с параметрами a=0 и ²=1. Найти а) E||; б) E^k, k=1,2,… Указание: Вывести рекуррентную формулу для E^k, используя интегрирование по частям . Ответ: , E^2k–1=0, E^2k=13…(2k–1).

9. Плотность распределения с.в.  имеет вид _(x)= в интервале (–c, c), _(x)=0 вне интервала. Найти E, D. Указание: замена x=csin t. Ответ: 0, c²/2.

10. Плотность распределения с.в.  имеет вид _(x)=xⁿe^–x/n! при x0, _(x)=0 при x<0. Найти E, D. Указание: – гамма функция, , n–натуральное. Ответ: n+1, n+1.

11. Пусть – непрерывная случайная величина с плотность распределения _(x) на отрезке [a, b], _(x)=0 вне отрезка. Доказать, что aEb.

12. Случайная величина  имеет конечный второй момент E². Найти и то значение x, при котором этот минимум достигается. Указание: Воспользоваться равенством (доказав его) E(–x)²= E(–E)²+(x–E)². Ответ: = D= E(–E)².

13. Будем говорить, что случайная величина сосредоточенна на отрезке [a, b], если P{ab}=1 и при любом >0

P{a<a+}>0, P{b–< b}>0.

Доказать, что дисперсия случайной величины, сосредоточенной на отрезке длины l, не превосходит l²/4.

Указание: Пусть P{ab}=1, b– a=l. Воспользоваться тем, что D (зад. 12).

14. Показать, если – действительная случайная величина с конечным математическим ожиданием и f(x) – функция, выпуклая вниз, то , а если f(x) выпукла вверх, то . Указание: Воспользоваться тем, что выпуклая вниз функция f(x) удовлетворяет неравенству , –<x< + , где .

15. Случайные величины  и  имеют равномерное распределение на отрезке [0, 1]. Доказать, что при любом характере зависимости между  и  выполняется неравенство . Указание: Вычислить E|– 1/2| и E|– 1/2| воспользоваться неравенством |x–y || x|+|y |.

16. Показать, что для любых случайных величин ₁,…, _k с конечными r-ми (r1) моментами справедливо соотношение

.

Указание: Использовать выпуклость вниз функции f(x)=| x|^r и зад. 14.

17. Из урны, содержащей m белых и n–m черных шаров c возвращением извлекают b шаров. Пусть с.в. – число белых шаров среди извлеченных. Найти E, D. Ответ: ,

18. Из урны, содержащей m белых и n–m черных шаров без возвращения извлекают b шаров. Пусть с.в. – число белых шаров среди извлеченных. Найти E, D. Указание: Случайная величина _i=1, если i-й шар белый, и _i=0, если i-й шар черный. =₁+…+_b. (проверить) D_j=, . Ответ: , .

19. На конференции магов «Теория заговора‘2004» в одном ряду в зале заседаний, насчитывающем m+b мест, оказалось m колдунов и b ведьм, рассевшихся по своим местам случайно. Какое среднее число смежных мест занимают в этом ряду пары (пара: колдун–ведьма или ведьма– колдун). Указание: воспользоваться индикаторами. Ответ: .

20. (необязательно) Для использования шифра "Прямоугольная решетка" изготавливают из бумажного прямоугольника трафарет размером 6x10 клеток. Вырезанные клетки выбирают так, что при наложении трафарета на лист бумаги того же размера четырьмя возможными способами каждая клетка листа "открывается" ровно один раз. Первые 15 букв текста сообщения вписываются в прорези трафарета (по одной в каждую), потом трафарет поворачивается на 180 градусов, вписываются следующие 15 букв, трафарет переворачивается "наизнанку" и т.д. Результат зашифрования выглядит так:

Е	Е	И	С	А	Т	Ш	С	Я	И
К	О	Р	Т	Л	М	О	Р	Г	Е
Б	К	Б	Р	А	И	Н	И	У	А
О	Ч	К	И	С	Т	У	П	Т	Р
Ы		Е	О	О		С	Р	Л	Ь
Н	З	У	Ы	Ю		К			И

Какой текст был зашифрован?

21. (необязательно) Клара получила от Карла письмо по электронной почте. Из-за неправильной настройки компьютера то ли у Клары, то ли у Карла текст письма выглядел так:

Помогите Кларе прочитать письмо Карла.