17. Свойства отображения Вейля. Сведение проблемы вычисления кратного эк к проблеме дискретного логарифмирования в кп. Суперсингулярные кривые.

Отображение Вейля представляет собой билинейное отображение 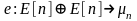, обладающее следующими свойствами:

• (билинейность)

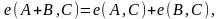
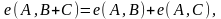
• e(P,P) = 1 для любого P ∈ E[n],

• (невырожденность) (∃P, Q ∈ E[n]) ,

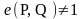• (вычислимость) e(X,Y ) может быть эффективно вычислено.

Если степень вложения k принимает небольшие значения (до k = 6), то для поиска ключа шифрования вместо решения задачи ДЛЭК можно решать более легкую задачу вычисления дискретного логарифма в конечном поле размерности q^k. Таким образом, эллиптические кривые, допускающие вложение в конечные поля с небольшой степенью k, не могут быть использованы в криптографии. Таковыми, например, являются все суперсингулярные кривые, имеющие степень вложения k ∈ {1, 2, 3, 4, 5, 6}.

Кривая 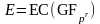называется суперсингулярной, если ее мощность #E = p^r + 1 − t, и p|t.

Примером суперсингулярной кривой может служить кривая E : 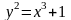(mod p), если характеристика поля p ≡ 2 (mod3), тогда E содержит p + 1 элемент, t = 0 и E имеет степень вложения, равную 2.

Способ вычисления дискретного логарифма на ЭК, использующий сведение Вейля, получил называние MOV-атаки.

Многие протоколы, использующие шифрование и электронные цифровые подписи на эллиптических кривых, специально запрещают использование суперсингулярных кривых. Таким образом, суперсингулярные кривые были изъяты из криптографии.

Однако в 2002 году А.Джоукс нашел неожиданное применение спариванию Вейля и суперсингулярным кривым для построения однораундового протокола выработки общего секретного ключа на основе метода Диффи-Хеллмана. Далее были найдены и другие, не менее интересные приложения такие, как, например, построение открытого ключа пользователя на основе его общеизвестных идентификационных данных таких, как, например, имя или адрес электронной почты (identity based open keys) (см. Advances in Elliptic Curve [?]).

Вычисление кратного точки ЭК с помощью MOV– алгоритма

Пусть заданы эллиптическая кривая EC : y2 = (modp^r), и точки P , Q ∈ EC порядка n, где n–простое число, причем существует m такое, что Q = mP . Требуется найти множитель m. Отображение Вейля будем обозначать через e(X,Y ). Алгоритм вычисления m заключается в

следующем:

1. Находим случайную точку

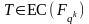
2. Находим порядок M точки T .

3. Находим d =Н.О.Д.(n,M). Если d = 1, то возвращаемся к п.1. Иначе, перейдем к следующему пункту. Определим, что в этом случае т.T имеет порядок n.

4. Вычислим a = e(P,T) и с = e(Q,T).

5. Вычисляя дискретный логарифм в поле 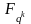, найдем искомый множитель m.

Отметим, что можно выполнять этот алгоритм с составным n, тогда число d может оказаться собственным делителем n и найденный множитель окажется равным m mod d. В этом случае можно повторять вычисление с различными точками T_i, вычисляя m_i = m mod di до тех пор, пока

произведение различных d_i не станет больше или равно n. После этого можно найти m с помощью китайской теоремы об остатках.

Замечание. Если речь идет о произвольной точке Q, то прежде, чем вычислять дискретный логарифм, полезно знать, найдется ли такое m, что Q = mP . Эту проверку можно выполнить, используя следующее утверждение:

Теорема 6.1. Для произвольной т. 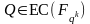найдется число m такое, что Q = mP в том и только в том случае, если выполняются два условия:

1. nQ = ∞,

2. e(P, Q) = 1.

19. Пусть Е: - эллиптическая кривая над алгебраически замкнутым полем К, n-положительное число и E[n] – подгруппа точек кривой Е порядка n:

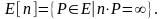(1)

Пусть точка 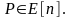Рассмотрим дивизор 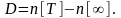Его степень равна 0, а сумма 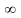. По теореме 6.2 найдется функция 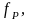дивизор которой равен D:

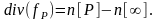(2)

Будем называть функцию удовлетворяющую (2), функцией Вейля.

Алгоритм Миллера вычисления функции Вейля

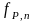
1. Найдем бинарное представление числа

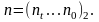
2. Определим исходные значения переменной Z и функции f равными P и 1 соответственно.

3. Выполняем цикл по i от i = t – 1 до i = 0:

Установим

Если 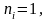тогда выполним операцию сложения P + Z:

4. Определим выходное значение функции Вейля

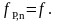
20. Преобразование Вейля. Пусть Е: - эллиптическая кривая над алгебраически замкнутым полем К, n-положительное число и E[n] – подгруппа точек кривой Е порядка n:

(1)

Пусть точка Пусть 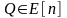не принадлежит орбите P, т.е не совпадает ни с каким кратным 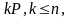точки Т. Рассмотрим дивизоры 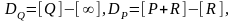где R – произвольно выбранная точка.

Опр.

Отображение Вейля – это билинейное отображение

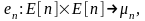
где 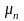- подгруппа по умножению корней n-й степени из 1 поля К, задаваемое следующей формулой: 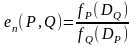или другой вид

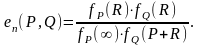
Преобразование Тейта. Пусть точка Обозначим через 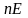множество точек 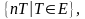а через 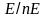мн-во классов эквивалентностей кривой Е по множеству .

Опр.

Отображение Тейта – это билинейное отображение 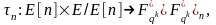где - подгруппа по умножению корней n-й степени 1 поля задаваемое следующей формулой: 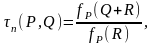где

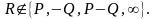
Важным отличием отображения Тейта от преобразования Вейля является то, что оно не вырождено (не равно 1) при P = Q.

21. Использование преобразования Вейля в трехстороннем протоколе Диффи-Хелмана.

Идея алгоритма Диффи-Хеллмана легко может быть обобщена на несколько участников. Приведем пример для случая n = 3:

1. Каждый из участников A, B, и C вырабатывает секретный ключ

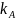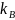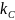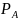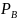, и соответственно и вычисляет точки = G, = G и

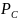= G, которые пересылает по циклу A к B, B к C, C к A.

2. Далее, участники A, B, и C вычисляют точки 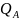= 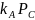, QB =

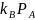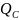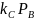, = соответственно и пересылают по тому же циклу.

3. На последнем шаге вычисляется общая точка R = 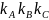G,

домножением точки, полученной на предыдущем шаге, на соответствующий

секретный ключ: R = G= = =

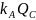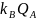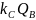
Замечание 1. Выполнение протокола Диффи-Хеллмана для двух

участников требует два обмена данными, для трех – уже шести обменов, а

для произвольного n – n! обменов данными, что является слишком большим

числом при сравнительно небольших n.

Основной ответ:

Протокол Диффи-Хеллмана генерации общего секретного ключа для трех

участников (Tripple Diffi–Hellman) с использованием преобразований Вейля–Тейта.

Рассматривается эллиптическая кривая EC :

и точка P большого порядка n.

Каждый из участников A,B и C выбирает случайное число , и

на интервале [2; n − 1] и вычисляет точку 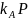, , 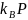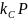соответственно, которую пересылает остальным участникам.

3. Теперь каждый участник вычисляет общий элемент конечного расширения поля ,

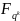где n|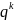 − 1 по формуле

k = = = =

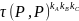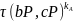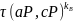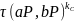
Выигрышем применения преобразований Вейля–Тейта является

уменьшение числа информационных обменов по сети (от 6 до 3).

22. Сведение проблемы вычисления кратного на ЭК к проблеме дискретного логарифмирования в конечных полях.

Пусть заданы эллиптическая кривая EC : ,

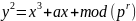и точки P , Q ∈ EC порядка n, где n–простое число, причем существует

m такое, что Q = mP . Требуется найти множитель m. Отображение Вейля

будем обозначать через e(X, Y ). Алгоритм вычисления m заключается в

следующем:

1. Находим случайную точку T ∈ EC( ).

2. Находим порядок M точки T .

3. Находим d =Н.О.Д.(n,M). Если d = 1, то возвращаемся к п.1.

Иначе, перейдем к следующему пункту. Определим, что в этом случае т.T

имеет порядок n.

4. Вычислим a = e(P, T) и с = e(Q, T).

5. Вычисляя дискретный логарифм в поле , найдем искомый

множитель m.

Отметим, что можно выполнять этот алгоритм с составным n, тогда

число d может оказаться собственным делителем n и найденный множитель

окажется равным m mod d. В этом случае можно повторять вычисление

с различными точками Ti , вычисляя mi = m mod di до тех пор, пока

произведение различных di не станет больше или равно n. После этого можно

найти m с помощью китайской теоремы об остатках.

Замечание. Если речь идет о произвольной точке Q, то прежде,

чем вычислять дискретный логарифм, полезно знать, найдется ли такое

m, что Q = mP . Эту проверку можно выполнить, используя следующее

утверждение:

Теорема.

Для произвольной т.Q ∈ EC(Fqk) найдется число m такое,

что Q = mP в том и только в том случае, если выполняются два условия:

1. nQ = ∞,

2. e(P,Q) = 1.

23.Вирусы, их виды и классификация.

Компьютерный вирус – это специальная программа, как правило очень маленького размера, способная внедряться в тело другой программы, перехватывать управление этой программой, саморазмножаться (распространяться) и внедряться в другие программы с задачей дестабилизации работы компьютера и порче информации.

Общая классификация

Анти-антивирусный вирус (Anti-antivirus Virus, Retrovirus) - компьютерная вирусная программа, объектом нападения которой являются антивирусные программы.

Вариант вируса, штамм, модификация (Variant, modification) - модифицированный вариант одного и того же вируса. Изменения в вирусный код могут вноситься как автором вируса, так и третьим лицом.

Вирусная программа-червь (Worm-virus) - паразитическая программа, обладающая механизмом саморазмножения. Программа способна размножать свои копии, но не поражать другие компьютерные программы. Проникает на компьютер из сети (чаще всего как вложение в сообщениях электронной почты или через сетьИнтернет) и рассылает свои функциональные копии на другие компьютерные сети.

Вирусный мистификатор (Hoax) - не являющееся вирусом почтовое сообщение. На компьютер пользователя мистификация приходит в виде письма, написанного в подчеркнуто нейтральном тоне, в котором указывается на якобы распространяющийся новый вирус. Большинство вирусных мистификаций обладают одной или несколькими нижеследующими характеристиками. Имя вируса, на которое ссылается автор сообщения, составляется не по правилам, используемым большинством антивирусных компаний. Особо отмечается, что "вирус" пока не обнаруживается антивирусными программами. Пользователю предлагается найти некий файл с помощью поискового средства Windows и удалить его с диска. В письме содержится призыв в случае обнаружения указанного файла сообщить об этом всем своим знакомым и все тем, чьи адреса есть в адресной книге пользователя. Несмотря на всю безобидность подобного розыгрыша опасность его очевидна - массовая рассылка копий этого бесполезного сообщения загружает почтовый трафик и отнимает время пользователей.

Вирусы-спутники, вирусы-компаньоны (Virus-companion) - формально являются файловыми вирусами. Не внедряются в исполняемые программы. Такие вирусы используют особенность системы DOS, позволяющую программному файлу с тем же названием, но другим расширением действовать с разными приоритетами. Под приоритетом понимают присваиваемый задаче, программе или операции признак, определяющий очередность их выполнения вычислительной системой. Большинство таких вирусов создают COM-файл, который обладает более высоким приоритетом нежели EXE-файлы с тем же самым названием. При запуске файла по имени (без указания расширения) будет запущен файл с расширением СОМ. Такие вирусы могут быть резидентными и маскировать файлы-двойники.

"Дроппер" (Dropper) - файл-носитель, устанавливающий вирус в систему. Техника, иногда используемая вирусописателями для "прикрытия" вирусов от антивирусных программ.

Зоологический вирус (Zoo virus) - вирус, существующий только в антивирусных лабораториях, в коллекциях исследователей вирусов и не встречающийся в "дикой природе".

Полиморфные вирусы (Polymorphic viruses) - или вирусы с самомодифицирующимися расшифровщиками (по Н.Н.Безрукову) - вирусы, использующие помимо шифрования кода специальную процедуру расшифровки, изменяющую саму себя в каждом новом экземпляре вируса, что ведет к отсутствию у него байтовых сигнатур. Расшифровщик не является постоянным - он уникален для каждого экземпляра вируса.

MtE вирусы (MtE viruses) - полиморфные вирусы, созданные с помощью генератора полиморфизма MtE (Mutant Engine). Такой генератор представляет собой специальный алгоритм, который отвечает за функции шифровки/расшифровки и генерацию расшифровщиков и присоединяется к любому объектному коду вируса. Такой расшифровщик не имеет ни одного постоянного бита, длина его всегда разная.

Pезидентный (в памяти) вирус (Memory resident virus) - постоянно присутствующий в памяти вирус, написанный, как правило, на языке Ассемблер или Си. Такие вирусы обладают возможностью более эффективно заражать программы и противодействовать антивирусным средствам. Занимает небольшой объем памяти. Пребывает в состоянии готовности к продолжению выполнения своей задачи до выгрузки, перезагрузки или выключения компьютера. Активизируется и выполняет заданные вирусописателем действия например при достижении компьютером определенного состояния (срабатывания таймера, др.). Все бутовые вирусы резидентны.

Скрипт-вирусы (Script virus) - вирусы, написанные на языках Visual Basic, Basic Script, Java Script. На компьютер пользователя такие вирусы, чаще всего, проникают в виде почтовых сообщений, содержащих во вложениях файлы-сценарии. Программы на языках Visual Basic и Java Script могут располагаться как в отдельных файлах, так и встраиваться в HTML-документ и в таком случае интерпретироваться браузером, причем не только с удаленного сервера, но и с локального диска.

Стелс-вирусы (Stealth virus) - вирусные программы, предпринимающие специальные действия для маскировки своей деятельности с целью сокрытия своего присутствия в зараженных объектах. Так называемая Стелс-технология может включать в себя:

затруднение обнаруженья вируса в оперативной памяти;

затруднение трассировки и дезассемблирования вируса;

маскировку процесса заражения;

затруднение обнаружения вируса в зараженной программе и загрузочном секторе.

Сегодня можно выделить два основных типа стелс-вирусов: руткит (rootkit) и буткит (bootkit).

Шифрованные вирусы (Encrypted viruses) - вирусы, которые сами шифруют свой код для затруднения их дезассемблирования и обнаружения в файле, памяти или секторе. Каждый экземпляр такого вируса будет содержать только короткий общий фрагмент - процедуру расшифровки - который можно выбрать в качестве сигнатуры. В случае каждого инфицирования он автоматически зашифровывает себя, и каждый раз по-разному. Таким способом вирус пытается избежать обнаружения антивирусными программами.

По видам заражаемых объектов

Файловые вирусы (File viruses) - вирусы, заражающие двоичные файлы (в основном, исполняемые файлы и динамические библиотеки). Чаще всего, такие файлы имеют расширение .EXE, .COM, .DLL, .SYS. Также могут инфицировать файлы с расширениями .DRV, .BIN, .OVL и .OVY. Такие вирусы внедряются в файлы операционной системы, активируются при запуске пораженной программы и затем распространяются.

Загрузочные (бутовые) вирусы (Boot viruses) - вирусы, которые заражают загрузочные записи (Boot record) дискет, разделов жестких дисков, а также MBR (Master Boot Record) жестких дисков.

Макрокомандные вирусы (макровирусы) (Macroviruses) - вирусы, заражающие файлы документов, используемыe приложениями Microsoft Office и другими программами, допускающие наличие макрокоманд (чаще всего на языке Visual Basic). Благоприятным фактором распространения вируса служит то, что все основные компоненты Microsoft Office могут содержать встроенные программы (макросы) на полнофункциональном языке программирования, а в Microsoft Word эти макросы автоматически запускаются при открытии любого документа, его закрытии, сохранении и т.д. Кроме того, имеется так называемый общий шаблон NORMAL.DOT и макросы, помещенные в общий шаблон автоматически запускаются при открытии любого документа. Учитывая то, что копирование макросов из документа в документ (в частности в общий шаблон) выполняется всего одной командой, среда Microsoft Word идеальна для существования макрокомандных вирусов.