
- •3. Метод rc4.
- •11. Вычисление кратного kQ заданной точки q
- •12. Шифрование сообщений с использованием эллиптических кривых
- •4.3.2. Неприводимые многочлены в конечном поле k.
- •18. Дивизоры
- •17. Свойства отображения Вейля. Сведение проблемы вычисления кратного эк к проблеме дискретного логарифмирования в кп. Суперсингулярные кривые.
1. Сетевая безопасность является частью информационной безопасности. Имея те же задачи, что и информационная безопасность, сетевая безопасность приобретает свою специфику, связанную с тем, что нападающий, оставаясь в тени своей географической удаленности или скрываясь за анонимными прокси- серверами, может действовать безнаказанно (или почти безнаказанно), нападая на различные службы и ресурсы сети путем целенаправленной атаки на отдельные компьютеры или проводя массированную бомбардировку своими пакетами диапазонов сети с целью выявления слабых бастионов. При работе с удаленными пользователями также изменяются стандартные процедуры аутентификации для локальных компьютеров, поскольку передача паролей в открытом виде становится опасной. Кроме того, пользователям инофрмационных сетей предлагаются все новые и новые услуги через сети GSM, беспроводные сети Wi-Fi, кабельный и спутниковый Интернет. Новые сервисы, представляя современному пользователю широкий спектр услуг, одновременно уменьшают его общую безопасность, расширяя базу незаконного внедрения извне для кражи паролей, конфиденциальной информации из компьютера пользователя, заражения его вирусами, троянскими конями, шпионскими модулями SpyWare, причиняющим индивидуальным пользователям и локальным сетям офисов и учреждений немалый экономический ущерб. Поэтому проблема надежной защиты от внешнего вторжения не является надуманной или малозначащей. В нашем курсе мы постараемся дать характеристику основным сетевым угрозам и соответствующим методам защиты. Перечислим сначало основные задачи информационной безопасности и дадим им краткую характеристику.
Под информационной безопасностью понимается защищенность информации и поддерживающей инфраструктуры от случайных или преднамеренных воздействий естественного или искусственного характера, которые могут нанести неприемлемый ущерб субъектам информационных отношений, в том числе владельцам и пользователям информации и поддерживающей инфраструктуры. Защита информации - это комплекс мероприятий, направленных на обеспечение информационной безопасности.
К основными задачами информационной безопасности относят следующие задачи:
1. Обеспечение доступности информационных ресурсов,
2. Обеспечение целостности информационных ресурсов и поддерживающей инфраструктуры,
3. Обеспечение конфиденциальности информационных ресурсов.
Поясним понятия доступности, целостности и конфиденциальности.
Доступность - это возможность за приемлемое время получить требуемую информационную услугу. Доступность информационных сервисов одновременно предполагает ограничение несанкционированного доступа, защиту сервисов от незаконного вторжения и захвата этих услуг.
Под целостностью подразумевается актуальность и непротиворечивость информации, ее защищенность от разрушения и несанкционированного изменения. Наконец, конфиденциальность - это защита от несанкционированного доступа к информации, чтения ее лицами, не имеющими соответвующих прав.
Информационные системы создаются для получения определенных информационных услуг. Если по тем или иным причинам предоставить эти услуги пользователям становится невозможно, это, очевидно, наносит ущерб всем субъектам информационных отношений. Поэтому, не противопоставляя доступность остальным аспектам, мы выделяем ее как важнейший элемент информационной безопасности.
2. Все методы шифрования принято делить на классические и методы шифрования с открытым ключем. Их также принято называть одно- и двух- ключевыми методами, поскольку в классическим шифрах для шифрования/расшифрования используется один и тот же ключ, в то время как в современных методах шифрования с открытым ключем используется два ключа – public key (публичный открытый ключ) и private key (личный закрытый ключ). Использование двух ключей позволяет преодолеть главный недостаток классических шифров – проблему распределения ключей. Методы, использующие один ключ, называются также симметричными, а использующие два ключа – асимметричными.
В свою очередь классические (одноключевые) методы шифрования делятся на две основные группы – потоковые и блочные. Потоковые методы шифруют входной поток данных посимвольно (или побитово). Шифрование каждого символа (бита) текста производится независимо от результата шифрования соседних символов (битов). Потоковые методы являются наиболее быстрыми, дешевыми и достаточно надежными методами шифрования.

Типичным представителем потокового метода шифрования является метод RC4 с переменной длиной ключа, разработанный в 1987 году Роном Ривестом из корпорации RSA Data Security, Inc. Этот метод широко используется в разных приложениях, например, в протоколе WEP для шифрования данных, передаваемым по беспроводным сетям Wi-Fi между точкой доступом (Access Point) и беспроводным адаптером на компьютере клиента. Ключом в методе RC4 является любая символьная последовательность длины до 256 байт, например, условная фраза или произвольный набор чисел. До 1994 года алгоритм RC4 держался в секрете и распространялся среди производителей под подписку о неразглашении, однако в 1994 году анонимный хакер опубликовал алгоритм метода в сети Usenet, после чего метод перестал был секретным. Однако это не ослабило его стойкость по отношению к атакам, и по настоящее время не найдено методов взлома RC4, которые были бы значительно лучше, чем полный перебор.
Этот метод имел ограничения по экспорту для использования с ключом более 40 байт, однако, нет никаких оснований предполагать, что ключ длины 40 байт является ненадежным, поскольку 40 байт=320 бит, а полный перебор 320-битового ключа лежит далеко за пределами сегодняшних возможностей и маловероятно, что когда-нибудь окажется возможным. Ниже мы опишем схему метода RC4.
3. Метод rc4.
Сам метод RC4 является чрезвычайно простым и легко программируется. Он состоит из начальной подготовки параметров шифрования - инициализации и собственно процесса шифрования. В ходе инициализации подготавливаются два числовых массива K и S длины 256 байт. При этом символьный ключ Key длины 64 или 128 символов кодируется в массиве S (в действительно, длина ключа здесь совершенно не влияет на работу алгоритма, и может быть принимать любое значение от 2 до 256). После этого связь между ключом Key и массивом S разрывается и в дальнейшем ключ Key не используется. Если взломщик узнает каким- нибудь образом массив S или его часть, он способен восстановить весь текст или его часть, но не сможет найти исходный ключ Key. Это позволяет использовать один и тот ключ Key многократно с разными исходными параметрами i, j, влияющими на сдвиг гаммирующей последовательности.
Инициализация.
Определяются два массива К и S длины 256 типа Byte.
Выбирается ключ Key, представляющий набор символов длины не более 256 байт.
Заполняем массив К кодами символом из ключа Key. Если длина ключа Key меньше 256, то используем ключ несколько раз (заполняя массив K полностью).
Инициализация S-блока. Сначала заполним его линейно:
S(0)=0, S(1)=1, … , S(255)=255
5. В цикле выполняем перестановку S-блока:
for i = 0 to 255:
j=(j + S(i) + K(i)) mod 256
'поменять местами S(i) и S(j)
temp=S(i): S(i)=S(j): S(j)=temp
Next i
Шифрование.
Организуем цикл, в котором считываем посимвольно текст, который надо закодировать, и одновременно генерируем ключевую последовательность, которая используется для сдвига символов текста:
‘ инициализируем начальные значения i,j произвольными значения от 0 до 255
i=i0: j=j0
Do while not eof(1)
i = (i +1) mod 256 j
j=(j + Si) mod 256
‘меняем местами S(i) и S(j)
temp=S(i): S(i)=S(j): S(j)=temp
t = (S(i) + S(j) mod 256
k=S(t)
‘ Считываем очередной символ из текста
m = Input(1, #1)
‘к ASCII-коду полученного символа m добавляет по модулю 256 элемент ключевой
‘последовательности k=S(t)
enc=(Asc(m)+k) mod 256
‘записываем в выходной поток закодированный символ
write #2, enc
End Do
Отметим, что ключевую последовательность метода RC4, называют также гамма-последовательностью, а процедуру шифрования – гаммированием
4. Тест Миллера Рабина. Пусть R – произвольное натуральное число. Представим R–1 в виде 2s∙t, где t – нечетно. Пусть a< R–1 – натуральное число. Будем говорить, что число a отвергает простоту R, если выполнено одно из двух условий:
а) R делится на a,
б)
 и для всех целых k,
и для всех целых k,

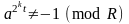 .
.
Если найдется число а, отвергающее R, то R является детерминировано составным. Иначе, число a подтверждает гипотезу о простоте числа R (т.е усиливает вероятность того, что R является простым). Поэтому тест Миллера-Рабина является вероятностным.
Тест Миллера состоит из отдельных проверок для различных a < R–1 и выполняется следующим образом:
Выполняем разложение R–1 = 2s∙t, где t – нечетное число.
Выбираем случайное число a, 1 < a < R-1. Проверим, что R не делится на а нацело. Если делится, то R – составное. Иначе, продолжим тест.
Вычисляем
 .
Если b
равно 1, то R
– вероятно простое число. Продолжаем
тест со следующим a.
Иначе, перейдем к следующему пункту.
.
Если b
равно 1, то R
– вероятно простое число. Продолжаем
тест со следующим a.
Иначе, перейдем к следующему пункту.Последовательно выполняем итерацию
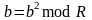 до тех пор, пока b
не станет равным R–1,
либо число итераций не превысит s-1,
где s
взято из пункта 1.
до тех пор, пока b
не станет равным R–1,
либо число итераций не превысит s-1,
где s
взято из пункта 1.
Если раньше выполнится b = R–1, то число R – вероятно простое, иначе R – составное.
Повторим процедуру с новым а.
После k циклов вероятность того, что R – составное, меньше 4-k, т.е. убывает очень быстро.
5. Метод RSA. Он основан на вычислительной сложности задачи разложения очень больших целых чисел на простые сомножители.
Генерация параметров метода.
Выбираем два больших простых числа p и q.
Вычисляем N = p∙q, и функцию Эйлера
 (значение
(значение
 равно количеству натуральных чисел k
< N,
взаимно простых с N).
равно количеству натуральных чисел k
< N,
взаимно простых с N).Находим число e, взаимно-простое с ,
Находим число d из условия наибольший общий делитель e ∙ d = 1 mod . Для нахождения d используем расширенный алгоритм Евклида. Для этого решим в целых числах уравнение
 .
(*)
.
(*)Значение d положим равным найденному b. Если множитель b окажется меньшим нуля, следует заменить его на
 .
.
Пара (N,e) объявляется открытым ключом и используется для шифрования. Параметр d является секретным и используется для расшифровки данных.
Шифрование
производится по формуле
 ,
где x – код исходного символа.
Раскодирование
производится по формуле
,
где x – код исходного символа.
Раскодирование
производится по формуле
 ,
и основано на теореме Эйлера
,
и основано на теореме Эйлера
 .
Проверим
вычисление. Из формулы (*)
.
Проверим
вычисление. Из формулы (*)
 получим
получим
 .
.
6.
Алгоритм шифрования ЭльГамаля. Он
базируется на трудности вычисления
дискретного логарифма. Для генерации
пары ключей сначала берется большое
простое число p и два случайных числа
g и x, каждое из которых меньше p. Затем
вычисляется
 .
Общедоступными ключами являются y,
g
и p,
а
секретным ключом является
х.
Для шифрования
сообщения M
выполняем следующее:
.
Общедоступными ключами являются y,
g
и p,
а
секретным ключом является
х.
Для шифрования
сообщения M
выполняем следующее:
Выбираем случ. число k, чтобы НОД(k, p-1)=1.
Вычисляем
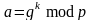 ,
,Вычисляем
 .
Пара
(a,
b)
является шифротекстом.
.
Пара
(a,
b)
является шифротекстом.
Для
расшифровки
шифротекста, вычисляем
 .
.
Сделаем
проверку:

Пример.
Выберем
p=11, g=2, секретный ключ x=8. Вычисляем
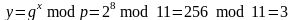 .
.
Пусть cообщение M=5. Выбираем случайное число K=9. Убедимся, что НОД(k, p-1)=НОД(9, 10)=1. Вычисляем пару (a, b):
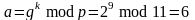 ,
,
 ,
(a, b)=(6, 9)-шифрограмма.
,
(a, b)=(6, 9)-шифрограмма.
Для расшифровки сообщения (a, b), находим
 ,
откуда,
,
откуда,
 .
Поскольку,
.
Поскольку,
 ,
то
,
то
 ,
откуда M=5.
,
откуда M=5.
7. Метод выработки секретного ключа Диффи-Хелмана. Выработка общего секретного ключа двумя пользователями, находящимя в условиях, когда все пересылаемые ими данные, доступны третьему лицу.
Сначала генерируются два больших простых числа n и q. Эти два числа не являются секретными. Далее один из партнеров A генерирует случайное число x<n и посылает другому участнику будущих обменов B значение M = qx mod n
Партнер B генерирует случайное число у<n и посылает A вычисленное значение K = qy mod n. Партнер A, получив K, вычисляет Cx = Kx mod n, а партнер В вычисляет Cy = My mod n. Алгоритм гарантирует, что числа Cy и Cx равны и могут быть использованы в качестве секретного ключа для шифрования.
Алгоритм Диффи-Хелмана, обеспечивая конфиденциальность передачи ключа, не может гарантировать того, что он прислан именно тем партнером, который предполагается. Для решения этой проблемы можно использовать технику электронной подписи. Например, сообщения M и K, которыми обмениваются пользователи, подписываются их цифровыми подписями, что исключает подлог.
