8. Использование мультиплексоров, дешифраторов и запоминающих устройств для построения логических функций.

Мультиплексор. На адресные входы мультиплексора подаются входные логические переменные Х1, Х2, Х3, а на информационных входах D0...D7 зафиксированы значения реализуемой логической функции на наборах логических переменных, номера которых совпадают с номерами информационных входов мультиплексора.

Таблица 1 истинности логической функции.

№ набора	X3	X2	X1	F
0	0	0	0	0	Y0
1	0	0	1	0	Y1
2	0	1	0	0	Y2
3	0	1	1	1	Y3
4	1	0	0	0	Y4
5	1	0	1	1	Y5
6	1	1	0	1	Y6
7	1	1	1	1	Y7

Имеется возможность вдвое сократить требуемое число информационных входов мультиплексора, если на эти входы подать не только фиксированные уровни логических единиц и нулей, но и значения отдельных входных переменных Х. Для этого еще раз изобразим таблицу истинности проектируемого мажоритарного элемента, разделив ее на четыре группы по две строки в каждой:

		(A2)	(A1)			Информационные входы мультиплексора
	№ набора	X3	X2	X1	F	D
Гр.1	0	0	0	0	0	D0=0
	1	0	0	1	0
Гр.2	2	0	1	0	0	D1=X1
	3	0	1	1	1
Гр.3	4	1	0	0	0	D2=X1
	5	1	0	1	1
Гр.4	6	1	1	0	1	D3=1
	7	1	1	1	1

В пределах каждой группы возможны только четыре значения выходной булевой функции F: нулевое значение на обоих наборах – гр. 1; единичное значение на обоих наборах – гр.4: совпадение функции F с переменной Х1 (наборы 2, 3, 4, 5): противоположные значения функции F и переменной Х1 (в данном примере отсутствуют). Следовательно, для реализации соответствующего КЦУ можно использовать четырехвходовой мультиплексор, на адресные входы которого подаются переменные Х3 и Х2, а на информационные входы D – значения в соответствии с последним столбцом таблицы (см. рис. слева).

Дешифратор. Так как активное значение сигнала на каждом выходе дешифратора определяет одну из комбинаций входных сигналов, то, объединяя с помощью соответствующих логических элементов некоторые выходные сигналы дешифратора, можно реализовать КС, заданное любой таблицей истинности, с числом наборов, не превышающим число выходов используемого дешифратора. Рассмотрим пример реализации трехвходового мажоритарного элемента (таблица 1 выше) на трехвходовом дешифраторе.

Для выходов дешифратора Yi с активными единичными значениями выходных сигналов (рисунок а) можно записать:

В таком случае в СДНФ функция мажоритарность в соответствии с таблицей 1 может быть представлена в виде . Это выражение и реализует схема на рисунке слева.

Представим ту же функцию в СКНФ и произведем преобразования по теореме де Моргана:

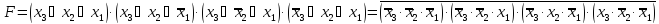
Проанализировав полученное выражение, а также выражения для Yi, приведенные выше, можно окончательно записать:/ В этом случае трехвходовой мажоритарный элемент может быть реализован на трехвходовом дешифраторе с активными нулевыми значениями выходных сигналов (рисунок б).

Если сравнить между собой реализации КС на основе мультиплексоров и дешифраторов, то можно отметить меньшие аппаратные затраты при использовании мультиплексоров. Однако в конкретных условиях проектирования КС может оказаться целесообразным применение для этих целей и дешифраторов, например, когда половина микросхемы сдвоенного дешифратора уже использована в составе проектируемого устройства, а другая половина осталась свободной и может быть применена для построения комб. схемы.

Запоминающее устройство. ПЗУ представляет собой большую интегральную схему (БИС), имеющую N входов и М выходов. Упрощенная структура ПЗУ при Nвх=2 и Мвых=3 на рисунке а). На входе схемы установлен дешифратор, преобразующий комбинации двухразрядного двоичного кода в четырехпозиционный унитарный (десятичный) код. При каждой комбинации входного ДК на одном из выходов дешифратора появляется логическая 1, а на остальных – нули.

Между выходами дешифратора k, l, m, n и выходными шинами ПЗУ X, Y, Z включены цепочки из двух последовательно включенных диодов VD1 и VD2. На рисунке б) в качестве примера показана связь между выходной шиной К дешифратора и выходом Х ПЗУ. В исходном состоянии цепочки, связывающие выходы дешифратора и выходы ПЗУ, ток не проводят и связи между шинами k, l, m, n и Х, Y, Z отсутствуют. При этом со всех выходов X, Y, Z снимаются логические нули.

Пользователь на специальном устройстве – программаторе – создает нужные связи между шинами, подавая пробивные напряжения между определенными точками. При этом соответствующие диоды пробиваются, например VD2 (рисунок б), и в дальнейшем могут рассматриваться как короткозамкнутые. На рисунке а) кружочками показаны созданные постоянные связи, реализующие таблицу истинности комбинационного устройства с тремя выходами:

N	B	A	X	Y	Z
0	0	0	1	0	1	k
1	0	1	0	1	0	l
2	1	0	1	1	1	m
3	1	1	1	0	0	n

Например, при комбинации входных логических переменных А=1, В=0 с выходов снимаются сигналы Х=0; Y=1; Z=0. Таким образом на ПЗУ можно реализовать нужную таблицу истинности комбинационного устройства, имеющего несколько выходов. Одна схема ПЗУ может заменить большое число логических микросхем малого и среднего уровня интеграции, поэтому ПЗУ могут эффективно использоваться для создания сложных комбинационных устройств. Кроме того, ПЗУ находят широкое применение как элементы постоянной памяти, в которые заносятся программы, управляющие работой микропроцессоров и однокристальных микроЭВМ.